
- •§ 16. Елементи теорії функцій комплексної змінної
- •16.1 Функції комплексної змінної.
- •16.1.1. Основні поняття
- •16.1.2 Границя і неперервність функції комплексної змінної
- •16.1.3. Основні елементарні функції комплексної змінної
- •16.1.3.1. Показникова функція
- •16.1.3.2. Логарифмічна функція
- •16.1.3.5. Тригонометричні функції
- •16.1.3.6. Гіперболічні функції
- •16.1.3.7. Обернені тригонометричні і гіперболічні функції
- •16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •16.1.5. Аналітична функція. Диференціал
- •16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
- •Приклади конформних відображень, що здійснюються деякими елементарними функціями див. Додаток 1.
- •16.2. Інтегрування функції комплексної змінної
- •16.2.1 Означення, властивості і правила обчислення інтеграла
- •16.2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •16.2.3. Інтеграл Коші. Інтегральна формула Коші
- •16.3. Ряди в комплексній площині
- •16.3.1. Числові ряди
- •16.3.2. Степеневі ряди
- •Ряд Тейлора
- •Нулі аналітичної функції
- •Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції
- •Усувні особливі точки
- •Істотно особлива точка
- •16.4. Лишок функції
- •16.4.1. Поняття лишка і основна теорема про лишки
- •16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
Істотно особлива точка
Якщо
 —
істотно особлива точка, то, як доводиться
(теорема Сохоцького-Вейерштраса), у
досить малому околі точки
—
істотно особлива точка, то, як доводиться
(теорема Сохоцького-Вейерштраса), у
досить малому околі точки
 функція
функція
 стає невизначеною. У такій точці
аналітична функція не має ні скінченної,
ні нескінченної границі. Вибираючи
різні послідовності точок
стає невизначеною. У такій точці
аналітична функція не має ні скінченної,
ні нескінченної границі. Вибираючи
різні послідовності точок
 ,
які збігаються до істотно особливої
точки
,
які збігаються до істотно особливої
точки
 ,
можна отримати різні послідовності
відповідних значень функції, що збігаються
до різних границь.
,
можна отримати різні послідовності
відповідних значень функції, що збігаються
до різних границь.
Приклад 16.
Визначити тип особливості
 в точці
в точці
 .
.
○ Функція
 в околі точки
в околі точки має наступний лоранівський розклад:
має наступний лоранівський розклад:
 (див. приклад 14). Точка
(див. приклад 14). Точка є істотно особливою точкою. Якщо
є істотно особливою точкою. Якщо
 вздовж додатньої частини дійсної осі,
то
вздовж додатньої частини дійсної осі,
то
 ;
якщо
;
якщо
 уздовж від’ємної частини дійсної осі,
то
уздовж від’ємної частини дійсної осі,
то
 .
.
Оскільки границя не існує, то маємо істотно особливу точку. ●
Зауваження.
Класифікацію ізольованих особливих
точок можна поширити на випадок, коли
особливою точкою функції
 є нескінченно віддалена точка,
є нескінченно віддалена точка,
 .
.
Околом
точки називають зовнішність якого-небудь
круга з центром у точці
називають зовнішність якого-небудь
круга з центром у точці
 і досить великим радіусом R (чим
більше R,тим меншший окіл точки
і досить великим радіусом R (чим
більше R,тим меншший окіл точки
 ).
).
Точку
 називають ізольованою особливою точкою,
якщо в деякому околі її немає інших
особливих точок функції
називають ізольованою особливою точкою,
якщо в деякому околі її немає інших
особливих точок функції
 .
.
Нескінченно
віддалена ізольована особлива точка
може бути усувною особливою точкою,
полюсом порядку m чи істотно особливою
точкою. У першому випадку лоранівський
розклад функції
 в околі точки
в околі точки
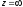 не має членів з додатніми показниками,
у другому — має їх лише скінчене число,
у третьому випадку в розкладі є нескінченно
багато членів з додатніми показниками.
не має членів з додатніми показниками,
у другому — має їх лише скінчене число,
у третьому випадку в розкладі є нескінченно
багато членів з додатніми показниками.
Вивчення функції
 в околі точки
в околі точки можна звести шляхом підстановки
можна звести шляхом підстановки
 до вивчення функції
до вивчення функції
 в околі точки
в околі точки
 .
.
Приклад 17.
Знайти особливі точки функції
 .
.
○ Особливою точкою
функції
 є
є
 .
Знайдемо границю функції при
.
Знайдемо границю функції при
 :
:
 .
Отже, точка
.
Отже, точка є полюсом. Можна переконатися, що
є полюсом. Можна переконатися, що
 ,
,
 .
Отже (див. (3.7)), точка
.
Отже (див. (3.7)), точка – полюстретього порядку. ●
– полюстретього порядку. ●
Приклад 18
Дослідити особливості функції
 .
.
○ Для даної функції
точки і
і
 —
прості полюсы,
—
прості полюсы,
 – полюс другого порядку. ●
– полюс другого порядку. ●
Приклад 19.
З'ясувати поведінку функцій
 ,
,
 в околі точки
в околі точки .
.
○ Зробимо підстановку
 .
Тоді функція
.
Тоді функція
 матиме вигляд
матиме вигляд
 .
При умові
.
При умові
 має місце розклад
має місце розклад
 .
Повертаючись до старої змінної, маємо
.
Повертаючись до старої змінної, маємо
 ,
,
 .
.
Тому
точка є усувною особливою точкою (див. останнє
зауваження).
є усувною особливою точкою (див. останнє
зауваження).
Неважко
переконатися, що
 для функції
для функції
 є правильною точкою. ●
є правильною точкою. ●
16.4. Лишок функції
16.4.1. Поняття лишка і основна теорема про лишки
Лишком
аналітичної функції
 в ізольованій особливій точці
в ізольованій особливій точці
 називається комплексне число, що
дорівнює значенню інтеграла
називається комплексне число, що
дорівнює значенню інтеграла
 ,
узятого в додатньому напрямку по колу
L з центром у точці
,
узятого в додатньому напрямку по колу
L з центром у точці
 ,
що лежить в області аналітичної функції
,
що лежить в області аналітичної функції
 (тобто в кільці
(тобто в кільці
 ).
).
Позначаються
лишки функції
 в ізольованій особливій точці
в ізольованій особливій точці
 символом
символом
 або
символом
або
символом
 .
Таким чином,
.
Таким чином,
Res
 (4.1)
(4.1)
Якщо у формулі
(3.12) покласти
 ,
то отримаємо
,
то отримаємо
 або
або
 ,
,
тобто
лишки функції
 відносно особливої точки
відносно особливої точки
 дорівнює коефіцієнту при першому члені
з від’ємним показником у розкладі
функції
дорівнює коефіцієнту при першому члені
з від’ємним показником у розкладі
функції
 в ряд Лорана (3.11).
в ряд Лорана (3.11).
Теорема
3.7
(Коші).
Якщо
функція
 є аналітичною в замкненій області
є аналітичною в замкненій області
 ,
обмеженій контуром L,
за винятком скінченого числа особливих
точок
,
обмеженій контуром L,
за винятком скінченого числа особливих
точок
 ,
що лежать усередині області D,
то
,
що лежать усередині області D,
то
 .
(4.2)
.
(4.2)
Навколо кажної
особливої точки
 опишемо коло
опишемо коло
 так, щоб воно повністю містилося в
області D, не містило усередині інших
особливих точок і щоб ніякі два з цих
кіл не мали спільних точок (див. рис.19)
так, щоб воно повністю містилося в
області D, не містило усередині інших
особливих точок і щоб ніякі два з цих
кіл не мали спільних точок (див. рис.19)
Тоді згідно теореми Коші для багатозв’язної області (наслідок 1 теореми 2.1) маємо:
 ,
,
де при інтегруванні всі контури обходяться проти годинникової стрілки. Але, відповідно до формули (4.1),
Маємо:
 ,
,
 ,
,
……………………
 .
.
Рис. 19
Отже,
 ,
тобто
,
тобто
 .
.
