Неопределенный интеграл.

Понятие неопределенного интеграла. Дифференцирование - это действие, с помощью которого по данной функции находится ее производная или диф­ференциал. Например, если F(x) = x¹⁰, то F' (х) = 10х⁹, dF(х) = 10х⁹ dх.

Интегрирование - это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если F' х = 7x⁶ , то F(х) = х⁷ , так как (х⁷)’ = 7х⁶ .

Дифференцируемая функция F(x), x ]a b[ называется первообразной для функции f(х) на интервале ]a; b[, если F'(x) = f(x) для каждого х] а; b [.

Так, для функции f{x) = 1/cos² х первообразной служит функция F(х) = tg х, поскольку (tg x)'= = 1/cos² x.

Совокупность всех первообразных функций f(x) на интервале ]а;b[ на­зывают неопределенным интегралом от функции f(x) на этом интервале и пишут f(x) dx = F(x) + С. Здесь f(x)dx -подынтегральное выражение; f(x )- подынтегральная функция; х - переменная интегрирования; С - произвольная постоянная.

Например, 5x’dx = х⁵ + С, так как (x⁵ + С)' = 5х¹.

Приведем основные свойства неопределенного интеграла.

1. Дифференциал неопределенного интеграла равен подынтегральному выражению:

d f(x)dx = f(x)dx.

2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т. е.

dF(x) =F(x + C.

3. Постоянный множитель можно выносить за знак неопределенного интеграла:

∫ af(x) dx = a ∫ f(x)dx.

4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:

∫ (f₁ (х) ± f₂ (x)) dx = ∫ f₁ (х) dx ± ∫ f₂ (x) dx.

Основные формулы интегрирования (табличные интегралы).

1.	∫ dx = x + C	7.
2.	∫ xndx = + С (п ≠ - 1)	8.
3.	∫ x-1dx =	9.
4.		10.
5.		11.
6.

Если интеграл затруднительно привести к табличному с помощью элемен­тарных преобразований, то в этом случае пользуются методом подстановки.

Пример 1. Найти

Решение. Произведем подстановку 2 - Зх² = t; тогда -6xdx = dt, xdx = -(1/6) dt. Далее, получаем

Пример 2. Найти

_{Решение. Сначала положим 2 + cos x = t; тогда 10dx = dt, откуда dx = (1/10) dt.}

_{Далее получаем}

Вопросы и упражнения для самопроверки:

1. Какое действие называется интегрированием?

2. Какая функция называется первообразной для функции f(х)?

3. Дайте определение неопределенного интеграла.

4. Перечислите основные свойства неопределенного интеграла.

5. Каким действием можно проверить интегрирование?

6. Напишите основные формулы интегрирования (табличные интегралы).

7. Найдите интегралы: a) 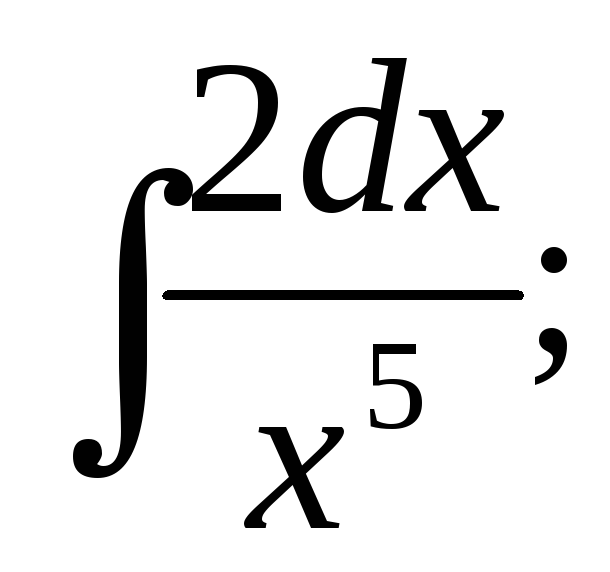б)

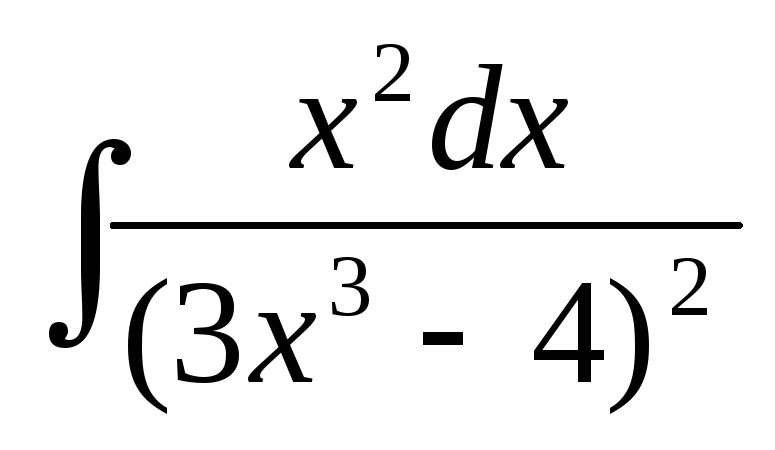
Определенный интеграл.

По данной теме сначала изучите §7-10 (1, 2), 11 (1, 2) гл. 3, §12, 14 (1 - 3) гл. 4 [3] или § 1 - 14 гл. 8 [4]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [3] гл. 3 §10 №3.5-3.8, 3.12, гл. 4 §12 № 4.1, §14 №4.3 - 4.29 или [4], гл. 8 №1-5, 8-13, 17-21, 23-27, 42-49, 50-55, 60-63.

Из контрольной работы выполните четвертое задание своего варианта.

Понятие определенного интеграла. Непосредственное вычисление определенного интеграла производится по формуле Ньютона—Лейбница;

где a - нижний предел, b - верхний предел, F(x) - какая-нибудь первообразная функции f(x).

Из этой формулы виден порядок вычисления определенного интеграла:

1. Находят одну из первообразных F(x) данной функции;

2. Находят значения F(x) при x = a и x = b;

3. Вычисляют разность F(b) – F(a).

Пример 1. Вычислить интеграл

Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:

Приведем основные свойства определенного интеграла.

1. Перестановка пределов интеграла знак интеграла меняется на противоположный:

2. Отрезок интегрирования можно разбивать на части:

3. Постоянный множитель можно выносить за знак интеграла:

4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:

Пример 2. Вычислить интеграл

Решение.

1. Произведем подстановку x³ + 2 = t; тогда 3x³dx = dt, x²dx =

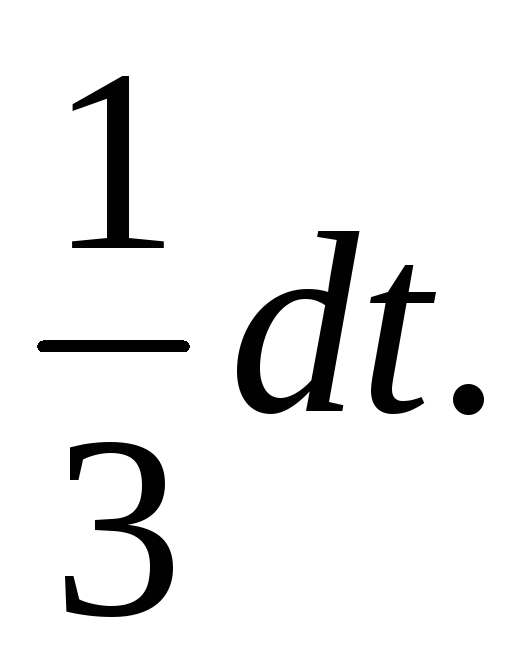
2. Определим пределы интегрирования для переменной t. При x = 1 получаем t_н = 1³+2 = 3, при x = 2 получаем t_в = 2³ + 2 = 10.

3. Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим:

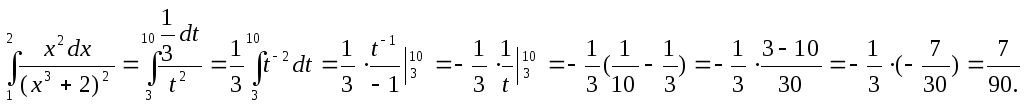
Пример 3. Вычислить интеграл

Решение.

1. Положим cos x = t; тогда -sin xdx = dt и sin xdx = -dt;

2. Определим пределы интегрирования для переменной t: t_H = cos 0 = t_H = cos (π/2) = 0.

3. Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим: