Функции и пределы.

Повторите понятия функции, области определения и области значений функции, а также §2 гл. 1 [2]. Изучите §15-19 гл. 4 [2], §4 гл. 3 и гл. 4, 5 [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решения приме­ров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [2] гл. 4 §15 № 4.1 - 4.3, 4.5 - 4.10, §18 № 4.35 - 4.37, 4.40 - 4.42, §19 № 4.43 - 4.44.

Из контрольной работы выполните первое задание своего варианта.

При вычислении пределов функций используются следующие теоремы:

1. Предел постоянной величины равен этой величине: lim с = с.

2. Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов этих функций:

(f₁ (x) ± f₂ (х) ± ... ± f_n (x)) = f₁ (x) ± f₂ (х) ± ... ± f_n (x).

3. Предел произведения конечного числа функций равен произведению пределов этих функций, если существуют конечные пределы сомножителей:

(f₁ (х) ∙ f₂ (х) … f_n (x)) = f₁ (x) ∙ f₂ (х) ... f_n (x).

4. Предел частного двух функций равен частному пределов этих функций, если предел делителя отличен от нуля и пределы делимого и делителя существуют:

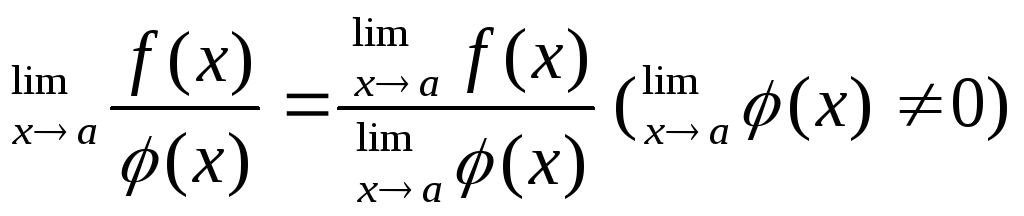
5. Постоянный множитель можно выносить за знак предела, т. е.

(c (∙ f (x)) = c ∙ f (х), где с = const, f (x) существует.

6. Если функция f(x) удовлетворяет неравенству

Ψ(x) ≤ f(x) ≤ φ(x) и если Ψ (x) = b, φ(x) =b, то f(x) = b.

Замечание: Функция f(x) может иметь только один предел при x, стремящемся к а.

Пример 1. Найти (5х² – 6x + 7).

Решение: Применяя теоремы о пределах, имеем

(5х² – 6x + 7) = (5x²) - (6x) + lim 7 =

= 5 х ∙ x - 6 x + lim 7 = 5∙3∙3 — 6∙3 + 7 = 34.

Пример 2. Найти

Решение: Теорему о пределе частного применить нельзя, так как при предел знаменателя равен нулю. Кроме того, и предел числителя равен нулю. Преобразуем дробь, разложив числитель на множители: 3x² – 3x – 18 = 3 (x+2) (x-3). Поэтому

_{Следовательно,}

_{Пример 3. Найти}

Решение: Преобразуем дробь, так как при предел числителя и предел знаменателя равен нулю. Имеем.

Следовательно,

Некоторые важные пределы:

где х – длина дуги или угол в радианах;

_{(число е – иррациональное).}

При практическом нахождении пределов функций приходится иметь дело с понятиями бесконечно малой и бесконечно большой функции. Если f(x) = 0, то функция f(x) называется бесконечно малой при . Если f(x) = ± ∞, то функция называется бесконечно большой при .

Если f(x) – бесконечно малая (бесконечно большая) при , то 1/f(x) – бесконечно большая (бесконечно малая) при .

Рассмотрим некоторые особые случаи нахождения предела функции.

Пример 4. Найти

Решение: Разделив почленно числитель и знаменатель на x³ (наивысшую степень x), получим

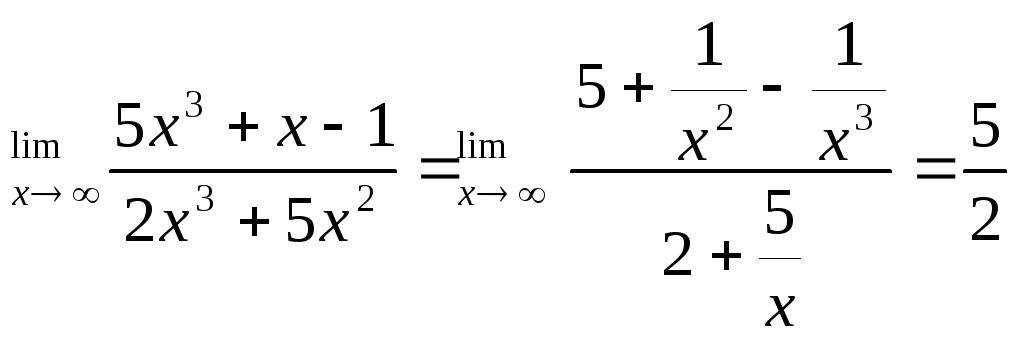
_{Аналогично находят предел при}

Пример 5. Вычислить

Решение: Сократим дробь на общий множитель:

Пример 6. Найти

Решение.