
- •§1. Функция, основные понятия.
- •§2. Основные свойства функций. Четность
- •Периодичность
- •§3. Предел функции. Раскрытие простейших неопределенностей.
- •§4. Сравнение бесконечно малых функций.
- •Говорят, что бесконечно малая a(X) имеет порядок k по сравнению с бесконечно малой b(X) при , если имеют одинаковый порядок малости бесконечно малые a(X) и (b (X))k, то есть
- •Дополнительные упражнения
- •Ответы.
- •§5. Замечательные пределы. Эквивалентные бесконечно малые функции.
- •§6. Односторонние пределы.
- •§7. Непрерывность функции в точке. Точки разрыва.
- •§8. Производная. Правила и формулы дифференцирования.
- •§9. Дифференциал функции, его применение.
- •§10. Дифференцирование неявных и параметрически заданных функций.
- •§11.Геометрический и механический смысл производной.
- •Пример 3
- •Из уравнения первой параболы получаем
- •Дополнительные упражнения
- •§12. Производные высших порядков.
§6. Односторонние пределы.
Число А
называется
левосторонним
пределом
функции f(x)
в точке
x = a,
если
![]() ,
то есть если
,
то есть если
![]() ,
что
,
что
![]() ,
оставаясь меньше
,
оставаясь меньше
![]() (
(![]() слева).
слева).
Обозначения:
![]() .
.
Число А
называется
правосторонним
пределом
функции f(x)
в точке
x = a,
если
![]() ,
то есть если
,
то есть если
![]() ,
что
,
что
![]() ,
оставаясь меньше
,
оставаясь меньше
![]() (
(![]() справа).
справа).
Обозначения:
![]() .
.
Левосторонний и
правосторонний пределы функции
![]() в точке
в точке
![]() называются ее односторонними пределами.
называются ее односторонними пределами.
Для существования
обычного
![]() необходимо и достаточно, чтобы оба
односторонних предела в точке
необходимо и достаточно, чтобы оба
односторонних предела в точке
![]() существовали и были равны, то есть чтобы
существовали и были равны, то есть чтобы
![]() .
.
Пример 1.
Найти односторонние пределы функции
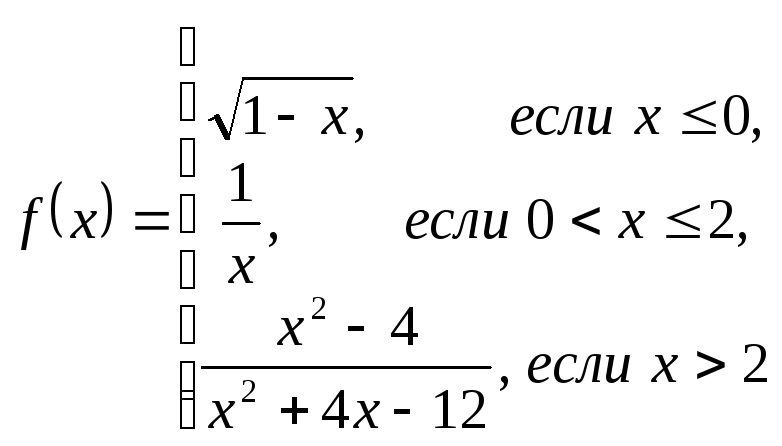 в точках
в точках
![]() и
и
![]() .
.
Сделать вывод о существовании предела функции в этих точках .
Решение.
При
![]() слева
слева
![]() ,
,
при
![]() справа
справа
![]() ,
,
следовательно
предел функции при
![]() не существует.
не существует.
При
![]() слева
слева
![]() ,
,
при
![]() справа
справа
![]()
![]() ,
,
односторонние
пределы при
![]() равны между собой, значит существует
предел данной функции
равны между собой, значит существует
предел данной функции
![]()
![]() .
.
Пример 2.
Найти односторонние
пределы функции
![]() при
при
![]() .
.
Решение.
Если
![]() (слева), то
(слева), то
![]() и
и
![]() ,
следовательно,
,
следовательно,
![]()
Если
![]() (справа), то
(справа), то
![]() и
и
![]() ,
тогда
,
тогда
![]()
Ответ:
![]() ,
,
![]()
Дополнительные упражнения.
Найти односторонние
пределы функции
![]() в точке
в точке
![]() .
Сделать вывод о существовании обычного
предела
.
Сделать вывод о существовании обычного
предела
![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Ответы.
а)
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]()
![]() ,
,
![]() не существует;
не существует;
в)
![]()
![]() ,
,
![]() не существует.
не существует.
§7. Непрерывность функции в точке. Точки разрыва.
Функция
![]() называется непрерывной
при
называется непрерывной
при
![]() (
в точке
(
в точке
![]() ),
если выполняются следующие условия:
),
если выполняются следующие условия:
-
функция
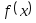 определена
в точке
определена
в точке
 и
в ее некоторой окрестности;
и
в ее некоторой окрестности; -
существует конечный предел функции
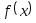 в точке
в точке
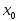 ;
; -
этот предел равен значению функции в точке
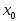 ,
т.е.
,
т.е.
![]() .
.
При этом точка
![]() называется точкой
непрерывности
данной функции.
называется точкой
непрерывности
данной функции.
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Точка
![]() называется точкой
разрыва функции
называется точкой
разрыва функции![]() ,
если эта
функция определена в некоторой окрестности
точки
,
если эта
функция определена в некоторой окрестности
точки
![]() ,
но не выполнено хотя бы одно из трех
условий непрерывности.
,
но не выполнено хотя бы одно из трех
условий непрерывности.
Классификация точек разрыва:
-
Если существует
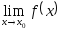 ,
но или
,
но или
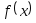 не
определена в точке
не
определена в точке
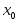 или
или
 ,
то
,
то
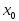 называют точкой
устранимого разрыва или
точкой разрыва типа
выколотой
точки.
называют точкой
устранимого разрыва или
точкой разрыва типа
выколотой
точки.
-
Если существуют конечные односторонние пределы, но они не равны , т.е.
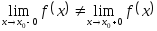 ,
то
,
то
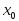 называют точкой
разрыва типа
скачка, а
разность
называют точкой
разрыва типа
скачка, а
разность
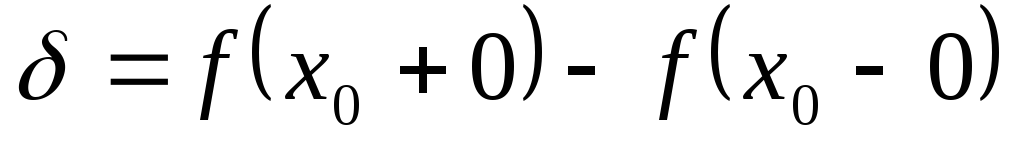 называется скачком
функции
называется скачком
функции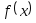 в точке
в точке 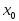 .
.
Разрывы типа выколотой точки и типа скачка относятся к конечным разрывам или к разрывам I рода.
-
Если в точке разрыва
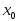 не существует или бесконечен хотя бы
один из односторонних пределов, то
не существует или бесконечен хотя бы
один из односторонних пределов, то
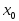 называют точкой
разрыва 2-го рода.
называют точкой
разрыва 2-го рода.
Из свойств непрерывных функций:
-
Все основные элементарные функции: показательная, логарифмическая, степенная, тригонометрические, обратные тригонометрические непрерывны на своих областях определения.
-
Все элементарные функции (они получаются из основных элементарных функций арифметическими операциями и суперпозициями) также являются непрерывными во всех точках своей области определения.
Пример 1.
Доказать, что
функция
![]() непрерывна при всех
непрерывна при всех
![]() .
.
Решение.
Выберем произвольную
точку
![]()
![]() и покажем, что для нее выполняются все
три условия, приведенные в определении
непрерывности функции в точке:
и покажем, что для нее выполняются все
три условия, приведенные в определении
непрерывности функции в точке:
1) т.к. функция
![]() определена на всей числовой оси, то
точка
определена на всей числовой оси, то
точка
![]() со
своей окрестностью входит в область
определения;
со
своей окрестностью входит в область
определения;
2) применяя теоремы о пределах суммы и произведения, найдем
![]() ;
;
3)
![]()
![]() .
.
Получили, что
![]() - точка непрерывности функции, а в силу
произвольности выбора
- точка непрерывности функции, а в силу
произвольности выбора
![]() данная
функция непрерывна при всех
данная
функция непрерывна при всех
![]() .
.
Пример 2.
Дана функция
![]() .
.
При каких значениях
А функция
![]() будет непрерывной в точке
будет непрерывной в точке
![]() ?
?
Решение.
В точке
![]() и ее окрестности функция определена,
и ее окрестности функция определена,
![]() .
.
Вычислим ![]() .
.
Тогда данная
функция будет непрерывной в точке
![]() ,
если
,
если
![]() т.е. если А = 6.
т.е. если А = 6.
Ответ: А = 6.
Пример 3.
Найти область
непрерывности функции
![]() и ее точки разрыва.
и ее точки разрыва.
Решение.
Данная функция
является дробно-рациональной и относится
к элементарным функциям. Она определена
и непрерывна при всех значениях
переменной, когда знаменатель не
обращается в ноль, т.е. когда
![]() ,
то есть при
,
то есть при
![]() .
.
Рассмотрим точку
![]() ,
где функция не определена.
,
где функция не определена.
Вычислим
![]() ,
следовательно,
,
следовательно,
![]() – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
Ответ: функция
f(x)
непрерывна при
![]() ,
,
имеет бесконечный
разрыв в точке
![]() .
.
Пример 4.
Дана функция
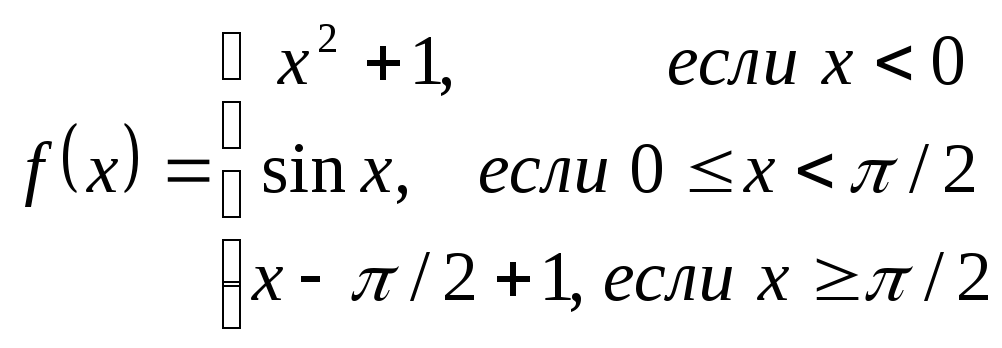 .
.
Найти промежутки непрерывности и точки разрыва функции. Построить ее график.
Решение.
Функция определена
при
![]() .
Она является непрерывной на интервалах
.
Она является непрерывной на интервалах
![]() ,
,
![]() и
и
![]() ,
на которых она задана непрерывными
основными элементарными функциями.
Следовательно, разрыв возможен только
в точках стыковки указанных интервалов,
то есть при
,
на которых она задана непрерывными
основными элементарными функциями.
Следовательно, разрыв возможен только
в точках стыковки указанных интервалов,
то есть при
![]() и
и
![]() .
.
Для точки
![]() имеем:
имеем:
![]() ,
,
![]()
Т.к. односторонние
пределы конечны и не равны между собой,
то в точке
![]() функция имеет разрыв 1-го рода.
функция имеет разрыв 1-го рода.
Для точки
![]() находим:
находим:
![]()
![]() .
.
![]() .
.
Следовательно, в
точке
![]() функция непрерывна.
функция непрерывна.
График функции:
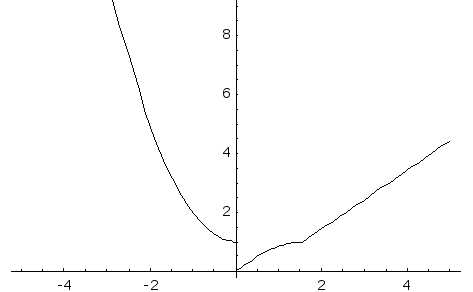
Ответ:
![]() непрерывна при
непрерывна при
![]() ,
в точке
,
в точке
![]() имеет разрыв типа скачка.
имеет разрыв типа скачка.
Пример 5.
Исследовать на
непрерывность функцию
![]() в точках
в точках
![]() и
и
![]() .
Сделать схематический чертеж.
.
Сделать схематический чертеж.
Решение.
Для точки
![]() имеем:
имеем:
![]()
![]() .
.
![]()
Следовательно, в
точке
![]() функция непрерывна.
функция непрерывна.
Для точки
![]() имеем:
имеем:
![]()
![]() не существует.
не существует.
Следовательно,
точка
![]() – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
Ответ: ![]() – точка непрерывности;
– точка непрерывности;
![]() – точка разрыва
2-го рода.
– точка разрыва
2-го рода.
Самостоятельная работа.
Вариант 1.
Исследовать на
непрерывность функцию
![]() в точках
в точках![]() и
и
![]() .
Построить график.
.
Построить график.
Вариант 2.
Исследовать на
непрерывность функцию
![]() в точках
в точках![]() и
и
![]() .
Сделать схематический чертеж .
.
Сделать схематический чертеж .
Вариант 3.
Исследовать на
непрерывность функцию
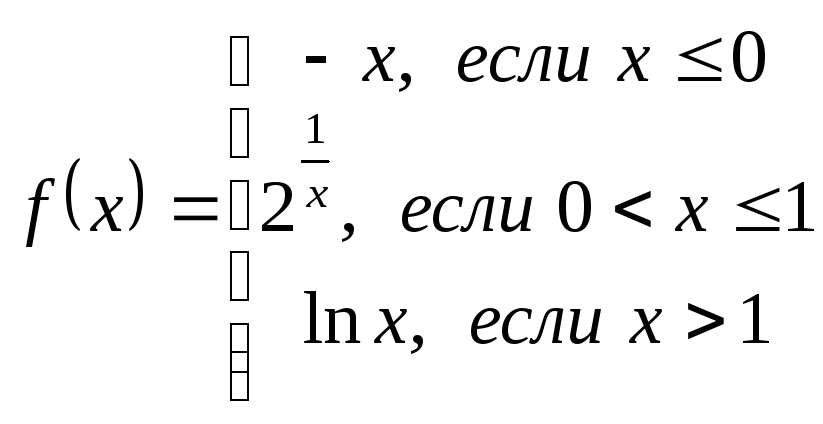 .
.
Построить график.
Ответы.
Вариант 1.
![]() - точка непрерывности,
- точка непрерывности,
![]() - точка устранимого разрыва.
- точка устранимого разрыва.
График:
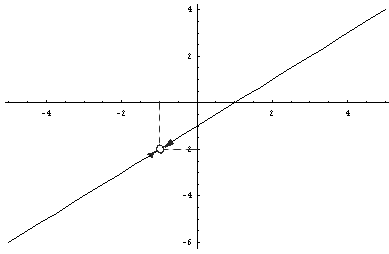
Вариант 2.
![]() -
точка непрерывности,
-
точка непрерывности,
![]() - точка разрыва 2-го рода.
- точка разрыва 2-го рода.
Чертеж:
Вариант 3.
![]() -
точка разрыва 2-го рода ,
-
точка разрыва 2-го рода ,![]() - точка разрыва типа скачка.
- точка разрыва типа скачка.
График:
Дополнительные упражнения.
-
Пусть
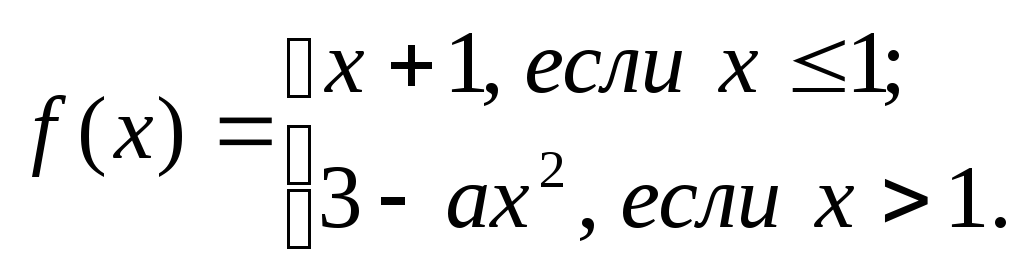
При каком выборе
числа «а» функция
![]() будет непрерывной? Построить ее график.
будет непрерывной? Построить ее график.
-
Охарактеризовать непрерывность функций
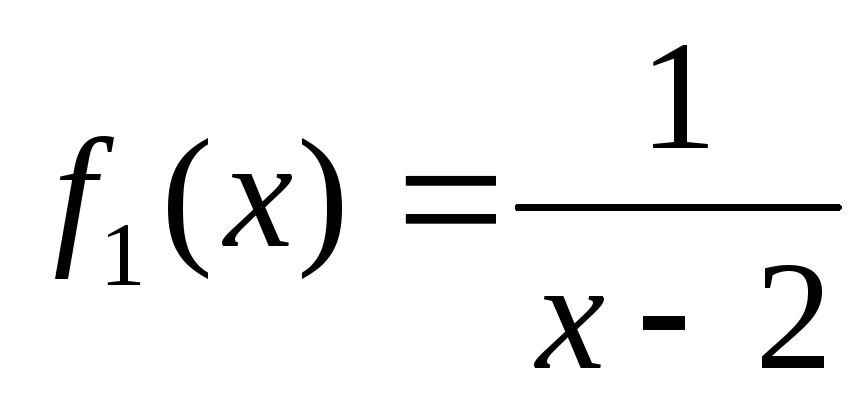 и
и
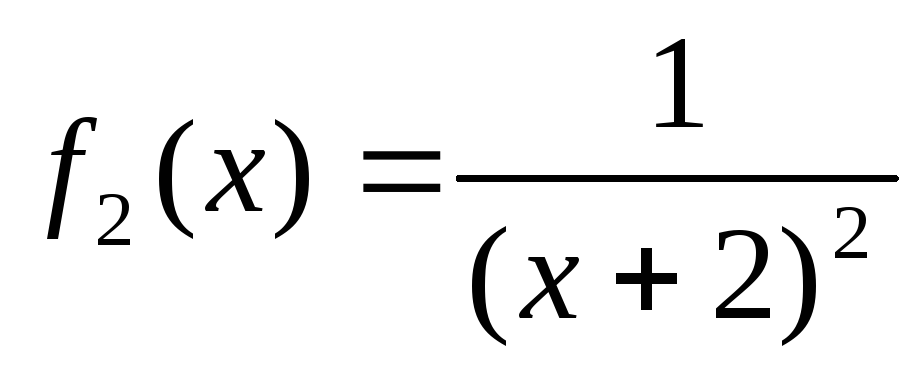 .
.
Построить их графики.
-
Охарактеризовать непрерывность функций
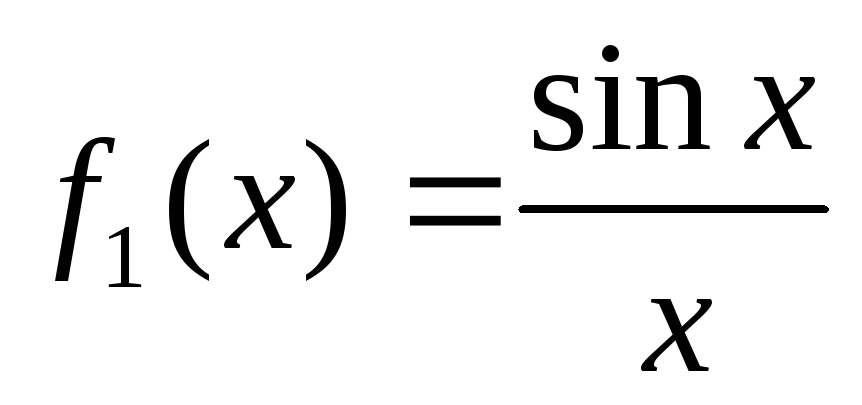 и
и
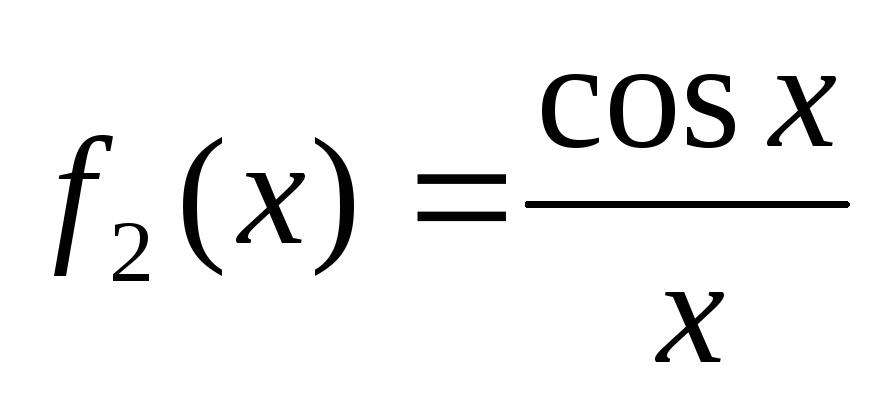 .
Построить их графики.
.
Построить их графики. -
Функция
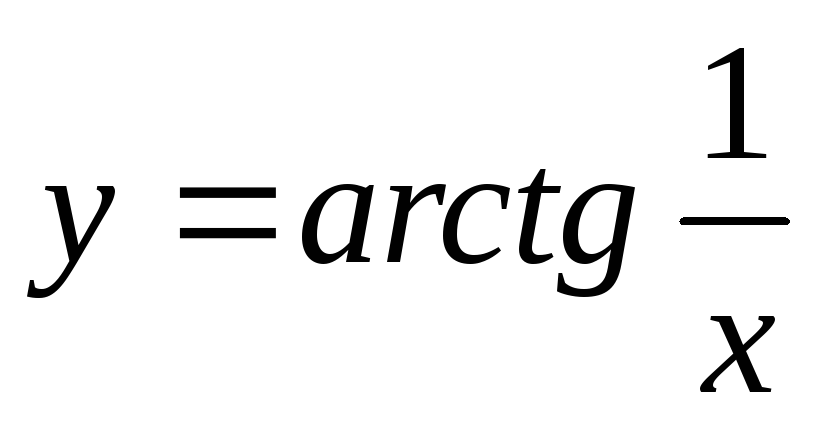 не определена при
не определена при
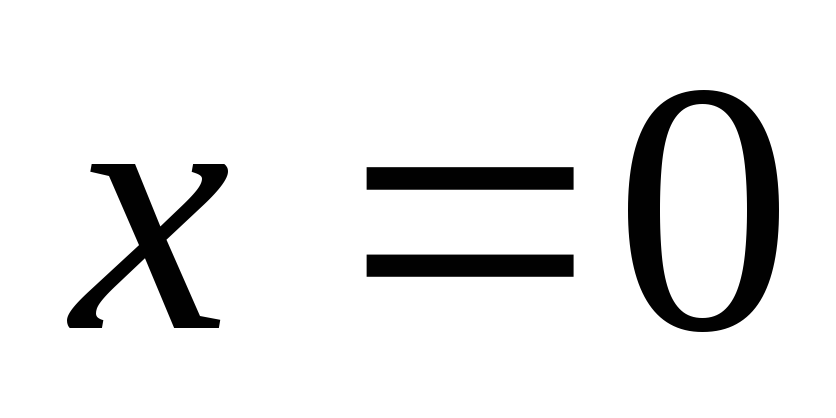 .
Какой разрыв имеет функция в точке
.
Какой разрыв имеет функция в точке
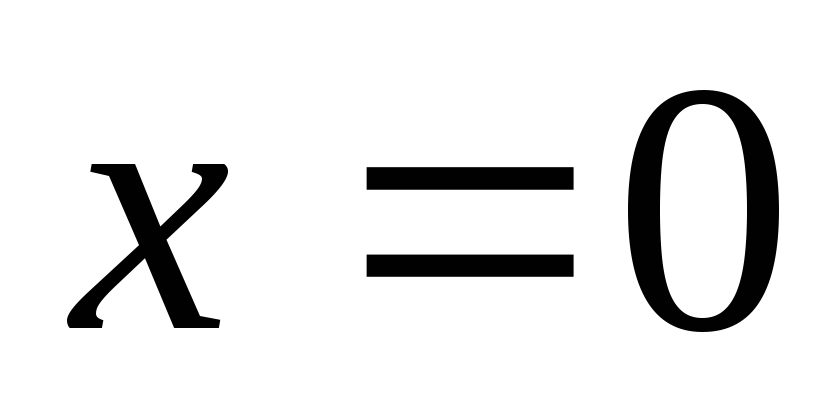 ?
? -
Описать непрерывность и построить графики функций
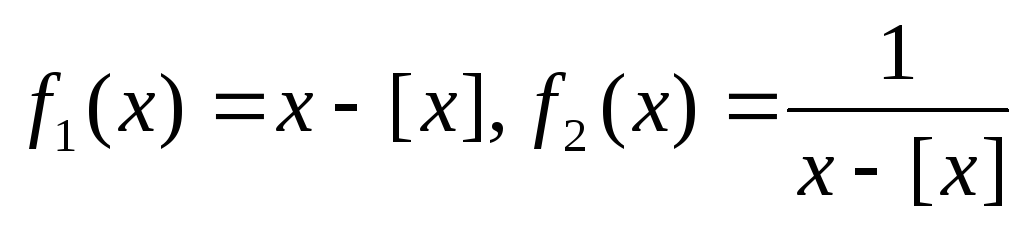 ,
где
,
где
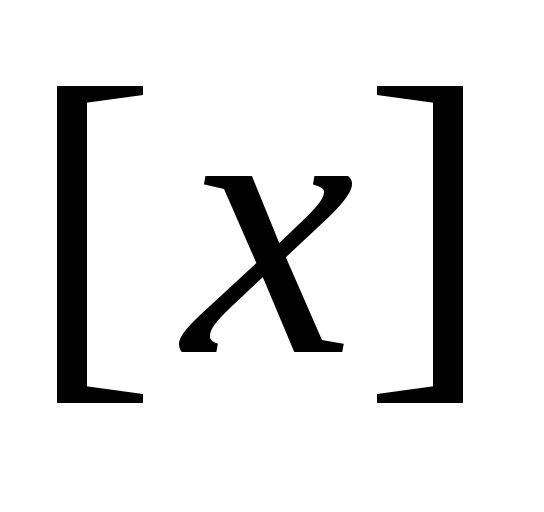 - это целая часть
- это целая часть
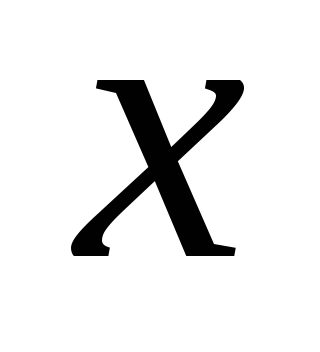 ,
она равна наибольшему целому числу, не
превосходящему
,
она равна наибольшему целому числу, не
превосходящему
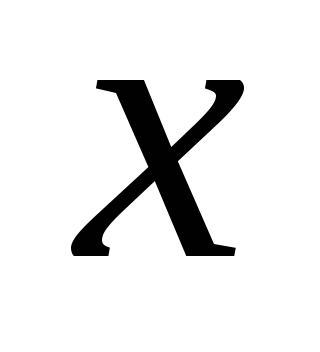 .
.
Ответы.
1. ![]() .
.
2. ![]() непрерывна при
непрерывна при
![]() ,
в точке
,
в точке
![]() имеет разрыв II
рода;
имеет разрыв II
рода;
![]() непрерывна при
непрерывна при
![]() ,
в точке
,
в точке
![]() имеет разрыв II
рода.
имеет разрыв II
рода.
3. ![]() непрерывна при
непрерывна при
![]() ,
в точке
,
в точке
![]() имеет устранимый разрыв.
имеет устранимый разрыв.
![]() непрерывна при
непрерывна при
![]() ,
в точке
,
в точке
![]() имеет разрыв II
рода.
имеет разрыв II
рода.
-
Разрыв типа скачка.
-
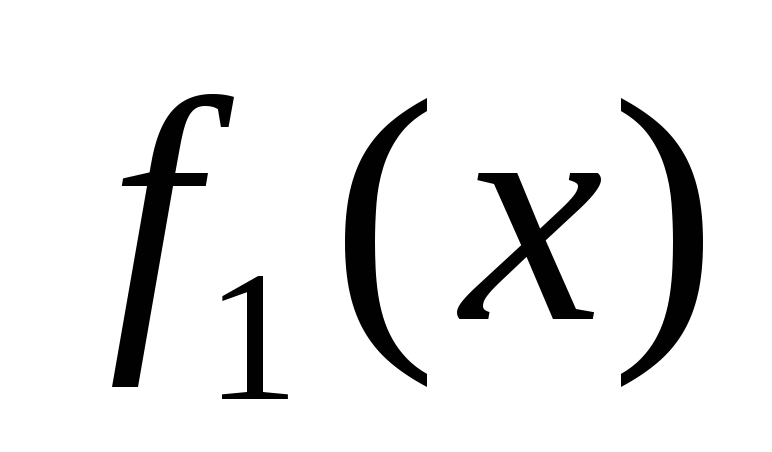 непрерывна при
непрерывна при
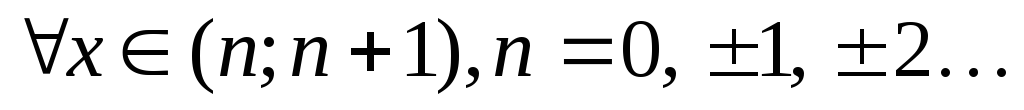 ;
имеет разрывы типа
;
имеет разрывы типа
скачка во всех
целочисленных точках
![]() ;
;
![]() непрерывна при
непрерывна при
![]() ;
имеет разрывы II
рода во всех целочисленных точках
;
имеет разрывы II
рода во всех целочисленных точках
![]() .
.
