
- •§1. Функция, основные понятия.
- •§2. Основные свойства функций. Четность
- •Периодичность
- •§3. Предел функции. Раскрытие простейших неопределенностей.
- •§4. Сравнение бесконечно малых функций.
- •Говорят, что бесконечно малая a(X) имеет порядок k по сравнению с бесконечно малой b(X) при , если имеют одинаковый порядок малости бесконечно малые a(X) и (b (X))k, то есть
- •Дополнительные упражнения
- •Ответы.
- •§5. Замечательные пределы. Эквивалентные бесконечно малые функции.
- •§6. Односторонние пределы.
- •§7. Непрерывность функции в точке. Точки разрыва.
- •§8. Производная. Правила и формулы дифференцирования.
- •§9. Дифференциал функции, его применение.
- •§10. Дифференцирование неявных и параметрически заданных функций.
- •§11.Геометрический и механический смысл производной.
- •Пример 3
- •Из уравнения первой параболы получаем
- •Дополнительные упражнения
- •§12. Производные высших порядков.
Атрощенкова И.Е., Кацуба В.С.
Практикум по высшей математике.
Функции одной переменной. Предел, непрерывность, дифференцируемость.
Оглавление
|
§1. Функция, основные понятия. §2. Основные свойства функций. §3. Предел функции. Раскрытие простейших неопределенностей. §4. Сравнение бесконечно малых. §5. Замечательные пределы. Эквивалентные бесконечно малые функции. §6. Односторонние пределы. §7. Непрерывность функции в точке. Точки разрыва. §8. Производная. Правила и формулы дифференцирования. §9. Дифференциал функции, его применение. §10. Дифференцирование неявных и параметрически заданных функций. §11. Геометрический и механический смысл производной. §12. Производные высших порядков. Список литературы. |
4 стр. 5 стр. 10 стр. 14 стр.
23 стр.
26 стр. 32 стр. 34 стр. 41 стр. 51 стр.
56 стр. 59 стр. 66 стр. 70 стр. |
§1. Функция, основные понятия.
![]()
![]()
![]()
![]()
Пусть дано числовое
множество
![]() ,
и пусть каждому
,
и пусть каждому
![]() поставлено в соответствие единственное
число
поставлено в соответствие единственное
число
![]() .
Тогда говорят, что на множестве
.
Тогда говорят, что на множестве
![]() определена числовая
функция.
определена числовая
функция.
Правило,
устанавливающее соответствие между
![]() и
и
![]() ,
обозначают некоторым символом, например,
,
обозначают некоторым символом, например,
![]() ,
и пишут
,
и пишут
![]()
В этой записи
![]() называют аргументом, или независимой
переменной; множество
называют аргументом, или независимой
переменной; множество
![]() называют областью определения функции,
обозначают
называют областью определения функции,
обозначают
![]() .
.
Число
![]() ,
соответствующее значению аргумента
,
соответствующее значению аргумента
![]() ,
называют значением
функции при
,
называют значением
функции при
![]() (значением
функции в
точке
(значением
функции в
точке
![]() )
и обозначают
)
и обозначают
![]() .Множество
значений функции обозначают
.Множество
значений функции обозначают
![]() .
.
Если функция
![]() определена
на области D,
G
– ее область значений, функция
определена
на области D,
G
– ее область значений, функция
![]() определена на области G,
то функция
определена на области G,
то функция
![]() называется
сложной
функцией, составленной
из функций
называется
сложной
функцией, составленной
из функций
![]() и
и
![]() ,
или композицией
функций
,
или композицией
функций
![]() и
и
![]() .
Сложная функция может быть композицией
большого числа функций.
.
Сложная функция может быть композицией
большого числа функций.
Если функция
![]() осуществляет взаимно однозначное
отображение области D
на область E,
то можно однозначно выразить
осуществляет взаимно однозначное
отображение области D
на область E,
то можно однозначно выразить
![]() через
через
![]() :
: ![]() .
Последняя функция называется обратной
по отношению к функции
.
Последняя функция называется обратной
по отношению к функции
![]() .
Для функции
.
Для функции
![]() Е является областью определения, а D
– областью значений. Обратную функцию
Е является областью определения, а D
– областью значений. Обратную функцию
![]() обычно переписывают в стандартном виде:
обычно переписывают в стандартном виде:
![]() ,
переобозначив ее аргумент через
,
переобозначив ее аргумент через![]() ,
а функцию через
,
а функцию через
![]() .
.
Функции вида
![]() называются
явными.
Уравнение вида
называются
явными.
Уравнение вида
![]() также задает функциональную зависимость
между x
и y
. В этом случае по определению
также задает функциональную зависимость
между x
и y
. В этом случае по определению
![]() называется неявной
функцией
называется неявной
функцией
![]() .
.
Графиком функции
![]() называется множество точек М(х
,y)
плоскости Оху
, координаты которых удовлетворяют
равенству
называется множество точек М(х
,y)
плоскости Оху
, координаты которых удовлетворяют
равенству
![]() .
.
К основным элементарным функциям относятся: степенные, показательные, логарифмические, тригонометрические, обратные тригонометрические и гиперболические функции.
Пример 1.
Дана функция
![]() .
Найти
.
Найти
![]() .
При каком значении
.
При каком значении
![]() функция не определена?
функция не определена?
Решение.
Для нахождения
значений функции надо подставить вместо
![]() значения
значения
![]() и вычислить:
и вычислить:
![]() ,
,
![]() .
.
Данная функция не
определена , если знаменатель дроби
обращается в ноль, т.е. при
![]() .
.
Пример 2.
Дана функция
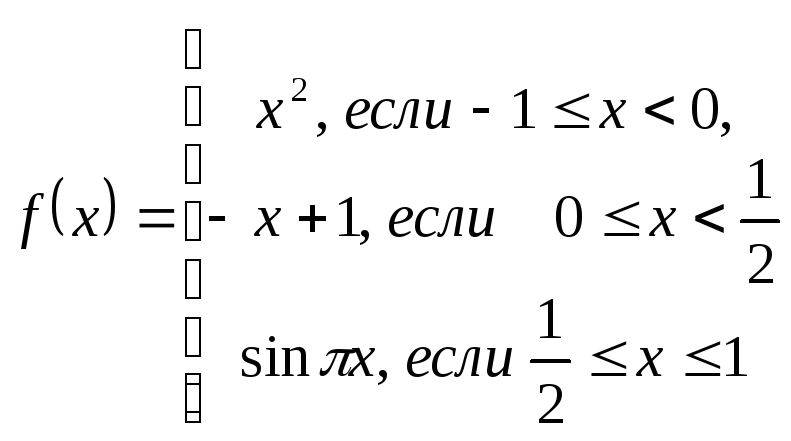 .
.
Найти
![]() .
Построить график функции.
.
Построить график функции.
Решение.
Функция
![]() определена на отрезке
определена на отрезке
![]() с
помощью трех формул, т.е. является кусочно
заданной.
с
помощью трех формул, т.е. является кусочно
заданной.
Так как значение
![]() ,то
,то
![]() .
.
Точка
![]() ,
поэтому
,
поэтому
![]() .
.
Точки
![]() и
и
![]()
![]() и, следовательно,
и, следовательно,
![]()
![]()
График функции:
Пример 3.
Найти область
определения функции : a)
![]() ;
;
б)
![]() ; в)
; в)![]() ; г)
; г)
![]() .
.
Решение.
а) Дробь определена
только в том случае, если ее знаменатель
не обращается в ноль, т.е. если
![]() .
Значит, областью определения функции
является множество всех действительных
чисел, кроме
.
Значит, областью определения функции
является множество всех действительных
чисел, кроме
![]() .
Записывают это так:
.
Записывают это так:
![]()
б) Так как квадратный
арифметический корень определен на
множестве неотрицательных чисел, то
должны одновременно выполняться
неравенства
![]()
![]()
![]() .
Таким образом,
.
Таким образом,
![]() .
.
в) Область определения
функции
![]() задается неравенством
задается неравенством
![]() .
Следовательно, нахождение области
определения данной функции сводится к
решению неравенства
.
Следовательно, нахождение области
определения данной функции сводится к
решению неравенства
![]() .
Возводя в квадрат, получим равносильную
систему:
.
Возводя в квадрат, получим равносильную
систему:
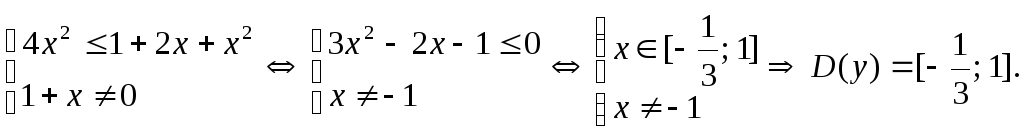
г) Логарифмическая
функция определена на множестве
положительных чисел, значит
![]() ,
т.е.
,
т.е.
![]() или
или![]() .
Таким образом,
.
Таким образом,
![]()
Пример 4.
Найти функции,
обратные данным : а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)![]() ,
г)
,
г)
![]() .
.
Решение .
а) Решая уравнение
относительно
![]() ,
получим:
,
получим:
![]() .
Эта функция и будет обратной для данной.
Переобозначив x
на y
и y
на x
в обратной функции, получим
.
Эта функция и будет обратной для данной.
Переобозначив x
на y
и y
на x
в обратной функции, получим
![]() .
.
б) По смыслу
уравнения, которым определяется функция
имеем что,
![]() и
и
![]() .
Возводя в квадрат, получим обратную
функцию
.
Возводя в квадрат, получим обратную
функцию
![]() .
Переобозначив ее аргумент и функцию,
получим
.
Переобозначив ее аргумент и функцию,
получим
![]() ,
где
,
где
![]() .
.
в) Данная функция
не задает взаимно однозначного
соответствия, т.к. различным значениям
x
из области определения D(y)=![]() могут соответствовать равные значения
y,
например,
могут соответствовать равные значения
y,
например,
![]() .
Значит, для нее нет обратной функции.
.
Значит, для нее нет обратной функции.
г) Эта функция на
указанной области определения
![]() задает взаимно однозначное соответствие
, т.е. каждому значению
задает взаимно однозначное соответствие
, т.е. каждому значению
![]() соответствует
единственное значение
соответствует
единственное значение
![]() .
.
Решим уравнение
![]() относительно
относительно
![]() :
:
![]()
![]()
![]()
![]() ,
,
но т.к.
![]() ,
то получим
,
то получим
![]() или, переходя к обычным обозначениям,
или, переходя к обычным обозначениям,
![]() ,
где
,
где
![]() .
.
Пример 5.
Представить сложные
функции в виде композиции основных
элементарных функций: а)
![]() ; б)
; б)
![]() .
.
Решение.
а)![]() ,
и тогда
,
и тогда
![]()
б)![]() ,
тогда
,
тогда
![]()
Пример 6.
Найти композиции
![]() и
и
![]() функций, заданных формулами: а)
функций, заданных формулами: а)![]() ; б)
; б)![]()
Решение.
а)![]()
б)![]()
Самостоятельная работа.
Вариант 1.
-
Найти область определения функций: а)
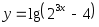 ;
;
б)![]() ; в)
; в)
![]() ; г)
; г)
![]()
-
Представить сложные функции в виде композиции основных элементарных функций: а)
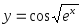 ; б)
; б)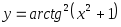 .
.
Вариант 2.
-
Найти область определения функций: а)
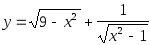 ;
;
б)![]() в)
в)![]() г)
г)![]() .
.
-
Представить сложные функции в виде композиции основных элементарных функций: а)
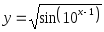 ; б)
; б)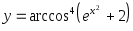 .
.
Вариант 3.
-
Найти область определения функций: а)
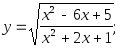
б)![]() в)
в)![]() ;
;
г)![]()
-
Представить сложные функции в виде композиции основных элементарных функций: а)
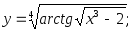 б)
б)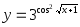 .
.

Ответы.
Вариант 1:
1а)![]() б)
б)![]() в)
в)![]() г)
г)![]()
Вариант 2:
1а)![]() ; б)
; б)![]() ; в)
; в)![]() г)
г)![]() .
.
Вариант 3: 1а)
![]() б)
б)![]() в)
в)![]()
г)
![]() .
.
