
- •§1. Функция, основные понятия.
- •§2. Основные свойства функций. Четность
- •Периодичность
- •§3. Предел функции. Раскрытие простейших неопределенностей.
- •§4. Сравнение бесконечно малых функций.
- •Говорят, что бесконечно малая a(X) имеет порядок k по сравнению с бесконечно малой b(X) при , если имеют одинаковый порядок малости бесконечно малые a(X) и (b (X))k, то есть
- •Дополнительные упражнения
- •Ответы.
- •§5. Замечательные пределы. Эквивалентные бесконечно малые функции.
- •§6. Односторонние пределы.
- •§7. Непрерывность функции в точке. Точки разрыва.
- •§8. Производная. Правила и формулы дифференцирования.
- •§9. Дифференциал функции, его применение.
- •§10. Дифференцирование неявных и параметрически заданных функций.
- •§11.Геометрический и механический смысл производной.
- •Пример 3
- •Из уравнения первой параболы получаем
- •Дополнительные упражнения
- •§12. Производные высших порядков.
§2. Основные свойства функций. Четность
Функцию
![]() ,
определенную на симметричном относительно
нуля множестве Х, называют четной,
если для любого
,
определенную на симметричном относительно
нуля множестве Х, называют четной,
если для любого
![]() верно равенство
верно равенство
![]() ,
и называют
нечетной,
если для любого
,
и называют
нечетной,
если для любого
![]() верно равенство
верно равенство
![]()
Если функция не является ни четной, ни нечетной, то ее называют функцией общего вида, или говорят, что функция свойством четности не обладает.
График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
Периодичность
Число
![]() называют периодом
функции f(x),
если для
любого
называют периодом
функции f(x),
если для
любого
![]() выполнены условия
выполнены условия
![]() и
и
![]() .
.
Функцию, имеющую период называют периодической.
Если Т
– период функции, то для любого
![]() число
nT
также является периодом этой функции.
число
nT
также является периодом этой функции.
Если функция имеет наименьший положительный период, то он берется в качестве основного.
График периодической функции с периодом Т функции при сдвиге вдоль оси абсцисс на Т переходит в себя.
Тригонометрические
функции
![]() и
и
![]() -
периодические с основным периодом T =
-
периодические с основным периодом T = ![]() , а
, а
![]() и
и
![]() -
с основным периодом T = .
-
с основным периодом T = .
Пример 1.
Исследовать функции
на четность: а)![]() ; б)
; б)![]() ;
;
в)
![]() при
при
![]()
Решение.
а) Функция определена
при
![]() ,
т.е. на множестве, симметричном относительно
начала координат и
,
т.е. на множестве, симметричном относительно
начала координат и
![]() .
.
Значит,
![]() – четная функция.
– четная функция.
б) Функция определена
при
![]() ,
т.е. на промежутке, симметричном
относительно 0;
,
т.е. на промежутке, симметричном
относительно 0;
![]() Значит,
Значит,
![]() - нечетная функция.
- нечетная функция.
в) Хотя формально
![]() ,
но эта функция не обладает свойством
четности, т.к. ее область определения
,
но эта функция не обладает свойством
четности, т.к. ее область определения
![]() несимметрична относительно начала
координат.
несимметрична относительно начала
координат.
Пример 2.
Определить, какие
из функций являются периодическими,
указать их наименьший период: а)![]() , б)
, б)![]() , в)
, в)
![]() ,
,
г)
![]() , д)
, д)
![]() , е)
, е)![]() .
.
Решение.
а) периодическая,
![]() ,
т.к. у функции
,
т.к. у функции
![]() основной период
основной период
![]() , то
, то
![]() ,
откуда
,
откуда
![]() ;
;
б) периодическая,
![]() ,
т.к. у функции
,
т.к. у функции
![]() основной период
основной период
![]() ,
то
,
то
![]() ,
откуда
,
откуда
![]() ;
;
в) непериодическая;
г) периодическая,
![]() ;
;
д) непериодическая;
е) периодическая,
![]() .
.
Самостоятельная работа.
Вариант 1.
1. Исследовать
функции на четность: а)![]() ; б)
; б)![]() ;
;
в)
![]() .
.
-
Найти основной период функции:
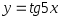 .
.
Вариант 2.
-
Исследовать функции на четность: а)
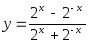 ;
;
б)![]() ; в)
; в)![]() .
.
-
Найти основной период функции:
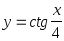
Вариант 3.
-
Исследовать функции на четность:
а)![]() ; б)
; б)![]() ; в)
; в)![]() .
.
-
Найти основной период функции:
 .
.
Ответы.
Вариант 1: 1а)четная;
б)нечетная; в) общего вида; 2)
![]() ;
;
Вариант 2: 1а)нечетная;
б) четная; в) общего вида; 2)![]() ;
;
Вариант 3: 1а) четная;
б)нечетная; в) общего вида; 2)
![]() .
.
Дополнительные упражнения.
-
Найти область определения функции: а)
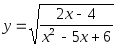 ;
;
б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
д)
![]() .
.
-
Исследовать функции на четность: а)
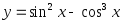 ;
;
б)![]() ; в)
; в)
![]() ; г)
; г)![]() .
.
-
Найти основные периоды функций: а)
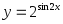 ; б)
; б)
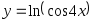 ;
;
в)![]() ; г)
; г)![]() .
.
Ответы.
1.а)![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)![]()
![]() ; д)
; д)
![]() .
.
2.а) четная; б) общего вида; в) четная; г) четная.
3. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
§3. Предел функции. Раскрытие простейших неопределенностей.
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
![]() .
.
Число А
называется пределом
функции
![]() при
при
![]()
(в точке
![]() ),
если для
любого
),
если для
любого
![]() ,
сколь малым бы оно ни было, существует
число
,
сколь малым бы оно ни было, существует
число
![]() ,
зависящее от
,
зависящее от
![]() ,
такое, что при
,
такое, что при
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
справедливо неравенство
,
справедливо неравенство
![]() .
.
Если А – предел
функции
![]() при
при
![]() ,
то пишут:
,
то пишут:
![]() или
или
![]() при
при
![]() .
.
В самой точке
![]() функция
функция
![]() может
и не существовать, т.е. значение функции
может
и не существовать, т.е. значение функции![]() может быть не определено.
может быть не определено.
Аналогично запись
![]() означает, что
означает, что
для любого числа
![]() ,
сколь малым бы оно ни было, существует
число
,
сколь малым бы оно ни было, существует
число
![]() ,
зависящее от
,
зависящее от
![]() ,
такое, что при всех
,
такое, что при всех
![]() справедливо неравенство
справедливо неравенство
![]() .
.
Говорят, что предел
функции
![]() в точке
в точке
![]() равен бесконечности, и пишут
равен бесконечности, и пишут
![]() ,
если
,
если
для любого числа
![]() ,
сколь большим бы оно ни было, существует
число
,
сколь большим бы оно ни было, существует
число
![]() ,
зависящее от M,
такое, что при всех x,
удовлетворяющих неравенству
,
зависящее от M,
такое, что при всех x,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]()
Справедливы следующие основные теоремы о конечных пределах.
Пусть существуют
![]() и
и
![]() ,
тогда
,
тогда
-

-
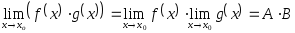
-
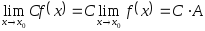 , где
, где

-
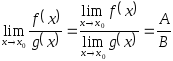 , если
, если
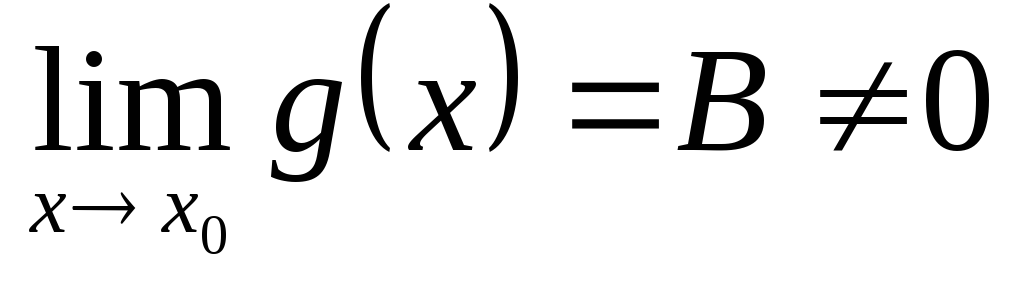
(Все теоремы верны
и при
![]() ).
).
Если некоторый предел не может быть вычислен ни по одной из о конечных пределах, ни по теоремам о бесконечно малых и о бесконечно больших функциях, то говорят, что этот предел имеет неопределенность, и указывает ее вид.
Основные виды неопределенностей:
![]() ,
,![]() ,
,![]() .
.
Чтобы вычислить предел, содержащий неопределенность, нужно эту неопределенность раскрыть, то есть преобразовать функцию, стоящую под пределом, так, чтобы неопределенность исчезла.
При вычислении пределов главная задача состоит в том, чтобы научиться раскрывать неопределенности.
Пример 1.
Доказать по
определению предела, что
![]() .
.
Решение.
Нам надо доказать,
что для любого числа
![]() ,
сколь малым бы оно ни было, существует
такое число
,
сколь малым бы оно ни было, существует
такое число
![]() ,
что из неравенства
,
что из неравенства
![]() следует неравенство
следует неравенство
![]() .
.
Зададим
![]() и составим неравенство
и составим неравенство
![]()
![]() .
.
Тогда если взять
![]() ,
то для всех значений
,
то для всех значений
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
будет выполняться неравенство
,
будет выполняться неравенство
![]() .
Следовательно,
.
Следовательно,
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Пример 2.
Найти
![]()
Решение.
Воспользуемся
теоремами о конечных пределах и получим,
что
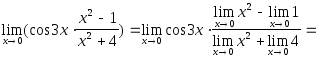
![]() .
.
Правило 1
Eсли
предел при
![]() рациональной дроби имеет неопределенность
рациональной дроби имеет неопределенность
![]() ,
то нужно числитель и знаменатель дроби
разложить на множители так, чтобы
выделить множитель
,
то нужно числитель и знаменатель дроби
разложить на множители так, чтобы
выделить множитель![]() ,
который стремится к нулю при
,
который стремится к нулю при
![]() ,
и сократить на него.
,
и сократить на него.
Пример 3.
Найти
![]() .
.
Решение.
Т.к. пределы
числителя и знаменателя равны 0 , применить
теорему о пределе частного нельзя, имеем
неопределенность вида ![]() .
Разложим числитель и знаменатель на
множители и сократим на общий множитель
.
Разложим числитель и знаменатель на
множители и сократим на общий множитель
![]() ,
который обращает в нуль числитель и
знаменатель. Получим
,
который обращает в нуль числитель и
знаменатель. Получим
![]()
![]() .
.
Пример 4.
Найти
![]()
Решение.
![]()
![]() .
.
Пример 5.
Найти
![]()
Решение.
Имеем неопределенность
вида
![]() .
Умножим числитель и знаменатель на
выражение, сопряженное числителю
.
Умножим числитель и знаменатель на
выражение, сопряженное числителю
![]() ,
чтобы, получив разность квадратов в
числителе и разложив на множители
знаменатель, сократить на
,
чтобы, получив разность квадратов в
числителе и разложив на множители
знаменатель, сократить на ![]() :
:
![]()
![]() .
.
Пример 6.
Найти
![]() .
.
Решение.
Имеем неопределенность
вида
![]() .
Умножим числитель и знаменатель на
неполный квадрат суммы выражения (
.
Умножим числитель и знаменатель на
неполный квадрат суммы выражения (![]() ),
чтобы получить в знаменателе разность
кубов. Далее выделим в числителе и
знаменателе множитель
),
чтобы получить в знаменателе разность
кубов. Далее выделим в числителе и
знаменателе множитель
![]() и сократим на него:
и сократим на него:
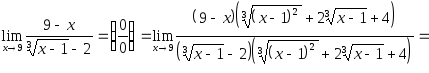
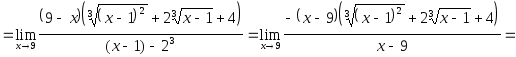
![]()
Правило 2
Чтобы раскрыть
неопределенность вида
![]() ,
образованную при
,
образованную при
![]() делением многочленов или иррациональных
выражений, нужно вынести за скобки в
числителе и знаменателе старшие степени
переменной x
и сократить дробь под знаком предела.
делением многочленов или иррациональных
выражений, нужно вынести за скобки в
числителе и знаменателе старшие степени
переменной x
и сократить дробь под знаком предела.
Пример 7.
Найти
![]() .
.
Решение.
Т.к. числитель и
знаменатель дроби неограниченно растут
при
![]() ,
то имеем неопределенность
,
то имеем неопределенность
![]() .Для
ее раскрытия вынесем за скобки в числителе
и знаменателе старшую степень переменной
.Для
ее раскрытия вынесем за скобки в числителе
и знаменателе старшую степень переменной
![]() и сократим на нее:
и сократим на нее:
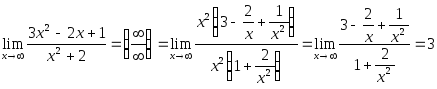 .
.
Здесь учтено, что
![]() и
и
![]() при
при
![]() .
.
Пример 8.
Найти
![]() .
.
Решение.
Аналогично
рассмотренному в предыдущем примере:
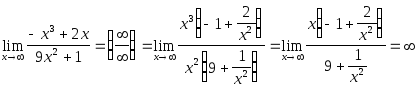
Пример 9.
Найти
![]() .
.
Решение.
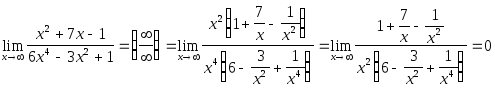
Пример 10. Обобщение результатов предыдущих примеров.
Найти
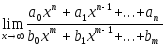 ,
где n
и m
– натуральные
числа,
,
где n
и m
– натуральные
числа,
![]() .
.
Решение.
Имеем неопределенность
![]() .
Вынесем за скобки в числителе
.
Вынесем за скобки в числителе
![]() ,
в знаменателе
,
в знаменателе
![]() и получим:
и получим:
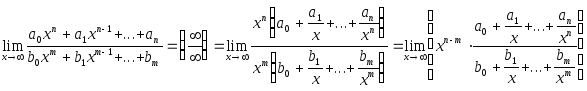
Предел второго
множителя равен
![]() .
Предел первого множителя зависит от
соотношения между числами
.
Предел первого множителя зависит от
соотношения между числами
![]() и
и
![]() :
:
если
![]() ,
то
,
то
![]() и, следовательно, общий предел бесконечен;
и, следовательно, общий предел бесконечен;
если
![]() ,
то
,
то
![]() и общий предел
и общий предел
![]() ;
;
если
![]() ,
то
,
то
![]() и общий предел равен нулю.
и общий предел равен нулю.
Итак, получен
результат, которым можно пользоваться
для раскрытия неопределенностей
![]() ,
образованных при
,
образованных при
![]() делением целых многочленов:
делением целых многочленов:
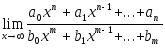
 .
.
Например,
![]() так как n = m = 3;
так как n = m = 3;
![]() так как n =5, m = 4,
то есть
n > m;
так как n =5, m = 4,
то есть
n > m;
![]() так как n =5,
m = 6,
то есть
n < m.
так как n =5,
m = 6,
то есть
n < m.
Правило 3.
Случай, когда
при
![]() или
или
![]() функция
функция
![]() представляет разность двух положительных
бесконечно больших величин, т.е.
неопределенность
представляет разность двух положительных
бесконечно больших величин, т.е.
неопределенность
![]() ,
можно привести к неопределенности
,
можно привести к неопределенности
![]() или
или
![]() путем преобразования функции к дроби.
путем преобразования функции к дроби.
Пример 11.
Найти
![]() .
.
Решение.
Так как знаменатель
каждой дроби есть величина бесконечно
малая при
![]() ,
а числители есть числа, не равные нулю,
то каждая из дробей является бесконечно
большой величиной, т.е. имеем неопределенность
,
а числители есть числа, не равные нулю,
то каждая из дробей является бесконечно
большой величиной, т.е. имеем неопределенность
![]() .
Чтобы раскрыть ее, приведем дроби к
общему знаменателю:
.
Чтобы раскрыть ее, приведем дроби к
общему знаменателю:
![]()
![]() .
.
Пример 12.
Найти
![]() .
.
Решение.
Имеем неопределенность
![]() .
Чтобы раскрыть ее, умножим и разделим
выражение на
.
Чтобы раскрыть ее, умножим и разделим
выражение на
![]() .
В результате получим:
.
В результате получим:
![]()
![]()
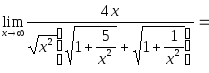
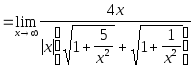 .
.
Т.к.
![]() ,
то дальнейшее решение надо проводить
отдельно для
,
то дальнейшее решение надо проводить
отдельно для
![]() и
и
![]() :
:
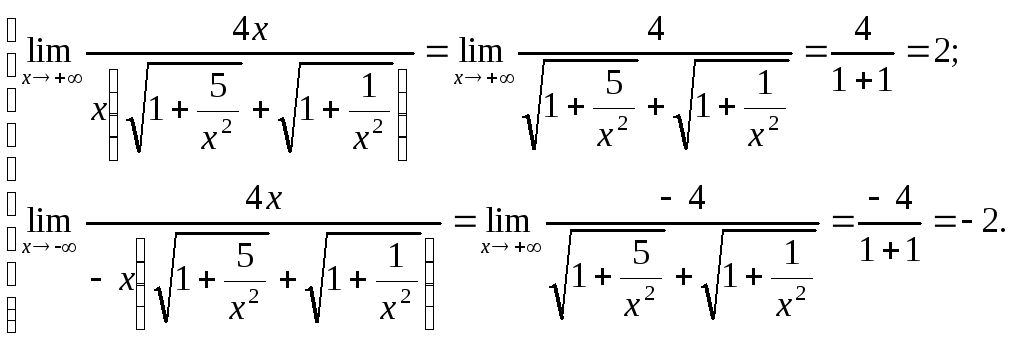
Пример 13.
Найти
![]() .
.
Решение.
При
![]() степень
числителя больше степени знаменателя
у обеих дробей /смотри пример 10 / ,значит
имеем неопределенность
степень
числителя больше степени знаменателя
у обеих дробей /смотри пример 10 / ,значит
имеем неопределенность
![]() .
Чтобы раскрыть ее , приведем дроби к
общему знаменателю:
.
Чтобы раскрыть ее , приведем дроби к
общему знаменателю:
![]()
(т.к. степени числителя и знаменателя равны, то предел равен отношению коэффициентов при старших степенях).
Самостоятельная работа.
Вариант 1.
Найти: а)![]() ;
б)
;
б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
Вариант 2.
Найти: а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
Вариант 3.
Найти: а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]()
Ответы.
Вариант
1: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)
![]() .
.
Вариант 2:
а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)
![]() .
.
Вариант
3: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() .
.
Дополнительные упражнения.
-
а)б)в)
 2.а)б)в)
2.а)б)в)
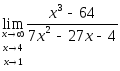
3.![]() 4.
4.
![]()
-
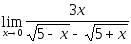 6.
6.
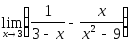
-
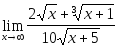 8.
8.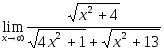
Ответы:
-
1. а)
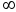 ,
б)
,
б)
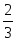 ,
в)
,
в)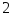 ;
;5.
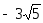 ;
;
2. а)
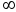 ,
б)
,
б)
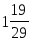 ,
в)
,
в)
 ;
;6.
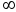 ;
;3. 7;
7.
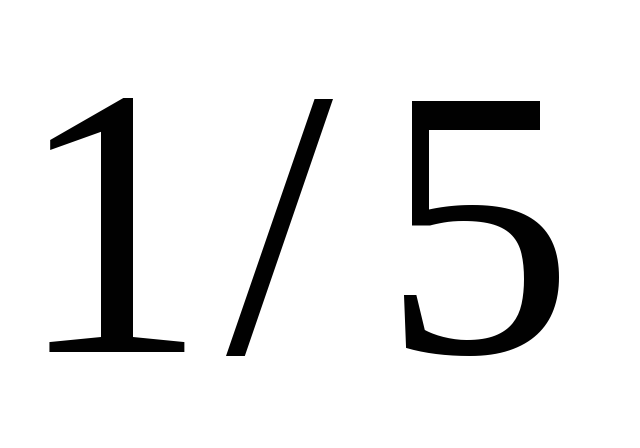 ;
;4.
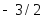 ;
;
8.
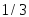 .
.
