
- •Квантовые теории Введение
- •История появления понятия «кванта»
- •Понятие кванта
- •Фотоэффект
- •Корпускулярно-волновой дуализм
- •Квантовая механика Математический аппарат квантовой механики
- •Операторы координаты и импульса
- •Принцип неопределенности Гейзенберга
- •Стационарное уравнение Шредингера
- •Амплитуда вероятности
- •Волновой пакет
- •Тождественность электронов
- •Принцип Паули
- •Спектроскопические опыты и введения понятия квантового числа
- •Квантовая теория поля
- •Кванты – переносчики взаимодействия
- •Понятие вакуумного состояния. Минимальная энергия поля
- •Квантование поля
- •Квантовая электродинамика (кэд)
- •Диаграммы Фейнмана
- •Рассеяние электрона на электроне
- •Рассеяние фотона на электроне
- •Рассеяние фотона на фотоне
- •Квантовая хромодинамика
- •Поляризация вакуума
- •Слабое взаимодействие
- •Лекция 7 в поисках новых законов
Стационарное уравнение Шредингера
Требуется найти оператор энергии для частицы, которая движется вдоль оси х со скоростью vx и энергией E в поле с потенциальной энергией V. Полная энергия частицы H равна сумме ее кинетической и потенциальной V(x) энергий:
H =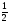 m
vx2+V(x).
m
vx2+V(x).
Воспользуемся тем, что импульс px= m vx и выразим кинетическую энергию через импульс:
H = 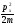 +V(x).
+V(x).
Учитывая,
что оператор импульса px ≡ 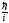
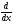 получим
получим
H ≡ 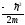
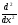 +V(x). (оператор
энергии)
+V(x). (оператор
энергии)
Чтобы найти собственные значения этого оператора надо решить уравнение для собственных значений.
 .
.
Удовлетворяющие данному уравнению значения E являются собственными числами оператора энергии, то есть совпадают со всевозможными допустимыми значениями энергии материальной точки. Если мы перенесем все в левую часть, то получим частный вид уравнения Шредингера:
 +
+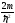 [E
— V(x)] ψ = 0.
[E
— V(x)] ψ = 0.
Это
стационарное уравнение Шредингера,
решение которого зависит от вида
потенциала V(x).
Если предположить, что частица движется
свободно, то есть, что потенциальная
энергия V(x)=0,
можно найти частный вид решения этого
уравнения: ψ(х) = х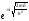 .
.
Видно, что решение этого уравнения — мнимая величина, но физическая величина должна быть вещественной. Мнимая величина не имеет физического смысла. Какой смысл имеет ψ – функция (волновая функция) до сих пор остается открытым вопросом. Проблема интерпретации этого результата называется проблемой ψ – функции. Физическую интерпретацию получил лишь квадрат ψ – функции:
|ψ|2 = ψ* ψ.
Он имеет смысл плотности вероятности обнаружить частицу в данной области пространства.
Амплитуда вероятности
Обычная вероятность описывает некоторую систему, которая может находиться в различных альтернативных состояниях. Вероятность – это действительное число, которое изменяется в пределах от нуля до единицы 0 ≤ p ≤ 1. Понятие вероятности в квантовой механике аналогично классическому, с той лишь разницей, что р – комплексное число.
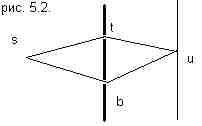
Вернемся к эксперименту с двумя щелями (рис. 5.2.). Какова классическая вероятность найти электрон в точке u? Если открыта только верхняя щель, она равна произведению вероятностей того, что электрон попадет из точки s в точку t , а из точки t в точку u.
P(s,t)× P(t,u)
Если открыта только нижняя щель, она равна произведению вероятностей того, что электрон попадет из точки s в точку b , а из точки b в точку u.
P(s,b)× P(b,u)
Если открыты обе щели, то полная вероятность равна сумме этих двух вероятностей
P(s,u) = P(s,t)× P(t,u)+ P(s,b)× P(b,u)
В квантовой механике правила вычислений будут аналогичными, но вместо вероятности будет стоять амплитуда вероятности.
A(s,u) = A(s,t)× A(t,u)+ A(s,b)× A(b,u)
Как
можно интерпретировать амплитуду
вероятности? Комплексное число z=x+iy
можно представить, в виде вектора с
началом в точке O
и концом в точке (x,y)
на комплексной
плоскости (см. рис. 5.3.).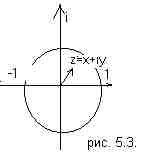
Для получения классической вероятности надо взять квадрат модуля амплитуды |z|2 = x2+y2, который является вещественным числом и, если необходимо, нормировать.
Если открыта только одна щель, то амплитуда того, что электрон попадет на экран, равна произведению амплитуд, что он из точки s попадет в точку t, а из точки t попадет в точку u: А(s, t)*А(t, u). Если открыта другая щель, то амплитуда будет равна А(s, b)*А(b, u). Квадрат модуля произведения равен произведению квадратов |zw|2 = |z|2|w|2,
Если
открыт более чем один маршрут, надо
образовать суммы. Сумма комплексных
чисел зависит от угла между ними
|w+z|2 = |w|2+|z|2+2|z||w|cos
θ, где –1<cos
θ<1.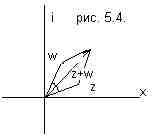
В тех областях экрана, где фазы колебаний совпадают, cos θ = 1 и волны усиливают друг друга. Освещенность в таких местах экрана возрастает в 4 раза. Там где волны находятся в противофазе cos θ = –1 и волны гасятся, образуя темную полосу нулевой освещенности. В промежуточных положениях освещенность убывает пропорционально разности амплитуд.
