3.3. Теоретичне і практичне значення ефективного рішення.

Поняття ефективного рішення є прямим узагальненням поняття точки максимуму числової функції на випадок декількох функцій.

Як правило, в прикладних задачах множина таких рішень виявляється не порожньою і, більш того, зовнішньо стійкою, і тому оптимальні рішення повинні вибиратися серед ефективних альтернатив.

Проте, якщо в однокритеріальній задачі як оптимальне можна брати будь-яке рішення, на якому критерій досягає максимуму, (оскільки вони еквівалентні), то в багатокритеріальній задачі, як правило, множина ефективних рішень виявляється дуже багатою нееквівалентними (і змістовно суттєво різними) рішеннями, і для осмисленого вибору оптимального рішення необхідно залучити більш повну інформацію про переваги.

І, тим не менше, поняття ефективного рішення грає найважливішу роль в теорії багатокритеріальної оптимізації.

Хоча ефективне рішення за звичай далеко не єдине, але все ж таки множина ефективних рішень значно вужча, ніж вихідна множина всіх рішень. Тому побудова множини ефективних рішень (або їх оцінок) є першим етапом великого числа процедур і методів багатокритеріальної оптимізації.

В разі наявності лише двох або трьох критеріїв множину ефективних оцінок можна зобразити графічно. Тому при аналізі двох, а інколи і трьохкритеріальних задач нерідко найзручніше обирати оптимальне рішення безпосередньо на основі розгляду графіку ефективних оцінок.

Такий підхід лежить, наприклад, в основі методу «вартість – ефективність».

Один з варіантів цього методу полягає в тому, що

• кожен зразок оцінюється по двох критеріях: вартості виробництва В і ефективності виконання поставлених задач Е. Значення цих критеріїв розраховуються за спеціально розрахованими методиками.

• будується графік оцінок, відповідних всім даним зразкам, а з| нього виділяються ті зразки, серед яких вибирається оптимальний

• остаточний вибір здійснюється ОПР на підставі аналізу графіка, оскільки він показує, якою ціною досягається підвищення ефективності.

Рис. 3.3. Графік оцінок проектів у методі «вартість – ефективність»

П р и к л а д  3.3. Нехай необхідно порівняти 6 проектів за критеріями «вартість–ефективність». Графік оцінок проектів наведено на рис. 3.3.

Оскільки критерій В (вартість) бажано мінімізувати, а критерій Е (ефективність) – максимізувати, то, як видно з графіку, перевагу мають проекти 1, 4, 3.

Звуження множини вибору до множини ефективних рішень (або деякої її підмножини) важливе не лише само по собі, але ще й тому, що на вужчій підмножині можуть виконуватися різного роду припущення, які спрощують подальший аналіз. Крім того ефективні рішення можуть мати цікаві і практично важливі властивості, яких немає у інших рішень.

П р и к л а д  3.4. Нехай є n галузей, зайнятих виробництвом n предметів (продуктів) споживання. Кожна галузь може виробляти один продукт, але за допомогою декількох виробничих процесів.

Позначимо через _і – множину виробничих процесів, доступних і-й галузі; множину _і будемо вважати скінченною.

Якщо прийняти загальну кількість трудових ресурсів за одиницю, то інтенсивність роботи і-ої галузі можна охарактеризувати величиною u_i   0, яка показує долю наявних трудових ресурсів, що використовуються в цій галузі. Ясно, що при повному використанні трудових ресурсів . Вектор u = (u₁, u₂, … , u_n) складові якого ненегативні і в сумі дорівнюють одиниці назвемо здійсненним.

Нехай 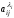– кількість j-го продукту, що виробляється і-ою галуззю, коли вона функціонує з одиничним рівнем інтенсивності (u_i = 1) і застосовується процес _i_i.

Припускаємо, що для i  j, але  > 0. Негативні інтерпретуються як кількість матеріалів (продуктів), що витрачаються у виробництві.

Вказане припущення про знаки означає, що кожна галузь може використовувати всі види матеріалів, тоді як виробляє лише| один продукт.

Вектор  = (, , 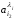… ) – називається вектором-процесом і-ої галузі.

Кожному виробничому процесу х_і відповідає свій вектор-процес.

Якщо для кожної галузі вибрано виробничий процес, тобто якщо зафіксовано набір  = (₁, ₂, … , _п), то чистий випуск продукту j всією системою буде

Квадратну матрицю, рядками якої є вектор-процеси, , i = 1, 2, … n, позначатимемо через А^. Тоді j-я компонента вектора c = uА^, є чистим випуском продукту j для фіксованого  і здійсненного вектора u.

Нехай А – множина матриць А^ кожна з яких відповідає певному набору  = (₁, ₂, … , _п), де _i  _i. Вектор (векторна оцінка) с = (с₁, c₂ … , с_п) називається таким, що реалізовується (або досяжним) якщо c = uА^, для деякої матриці А^l і здійсненного вектора u.

Особливо цікаві вектори с = (с₁, c₂ … , с_п), що реалізовуються, компоненти яких позитивні. Дійсно, якщо існує вектор с, що реалізовується , причому c_j > 0, j = 1, 2, … n, то це означає, що можна так організувати виробництво всіх продуктів, що кожна галузь вироблятиме продукту більше, ніж його потрібно для споживання всіма іншими галузями.

Розглянемо геометричну інтерпретацію цієї моделі.

Кожен вектор-процес можна подати у вигляді точки простору Еⁿ. Матриці А^l відповідає п таких точок (по одній для кожної галузі).

Вектор , є, вочевидь, точкою опуклої оболонки n векторів-процесів.

Таким чином множина векторів, що реалізовуються, с є об'єднанням опуклих оболонок векторів , які створюють матриці А^l  А.

Для ілюстрації розглянемо простий приклад з числовими даними.

П р и к л а д  3.5. Нехай в попередній задачі n = 2, ₁ = {1,2}, ₂ = {1,2,3}, a₁¹ = (2; –1), a₁² = (3/2; –2), a₂¹ = (–1; 1/2), a₂² = (–2; 3), a₂³ = (–4; 4).

Задача найкращого використання виробничих і трудових ресурсів полягає в тому, щоб забезпечити по можливості найбільший випуск всіх п продуктів, що виробляються галузями.

Розв’язування

Зобразимо на графіку (рис. 3.4) точки, які відповідають векторам-процесам . У нашому прикладі це точки a₁¹ = (2; –1), a₁² = (3/2; –2), a₂¹ = (–1; 1/2), a₂² = (–2; 3), a₂³ = (–4; 4).

Опуклим оболонкам цих векторів (тобто векторам с ) відповідають відрізки, які з’єднують ці точки.

Векторам с , що реалізуються, відповідають ті відрізки, що знаходяться в першій чверті. Очевидно, що максимум випуску продукції буде досягнуто при  = (1, 2) ( тобто перша галузь використовує перший процес, а друга галузь – другий процес) і будь-який ефективний план є парою (, u), де u = (u₁, u₂), 0,5 < u₁ < 0,75, u₂ = 1 – u₁ (ці умови забезпечують реалізуємість вектора с).

Рис. 3.4. Графічна ілюстрація до прикладу 3.5.

Таким чином, план x = {, u}, де  – виробничі процеси, и – здійсненний вектор, характеризується векторним критерієм с(х) = (с₁(х), … , с_n(х)), де с_j – чистий випуск j-го продукту.

План х* називається ефективним, якщо не існує здійсненного вектора и і матриці А*, для яких с(х)  с_j(х^*), причому принаймні одна з цих нерівностей – строга. Вектор с(х^*), що відповідає ефективному плану х*, також називається ефективним.

Структура ефективних векторів з позитивними компонентами характеризується таким твердженням: якщо існує вектор, що реалізовується, з позитивними компонентами, то всі ефективні вектори з позитивними компонентами лежать в опуклій оболонці вектор процесів , що складають матрицю А′ А, і кожна точка цієї опуклої оболонки, що знаходиться в позитивному октанті є ефективним вектором.

Тобто, якщо є допустимий план, що забезпечує випуск кожного продукту з лишком, то для кожної галузі є певний виробничий процес (що входить в набір ′), що дозволяє отримати всі ефективні вектори з позитивними компонентами лише за рахунок перерозподілу трудових ресурсів.

Іншими словами, будь-який ефективний план, що забезпечує випуск кожного продукту з лишком, або має вигляд (, u), де u – деякий здійсненний вектор, або еквівалентний плану вказаного виду.