РОЗДІЛ 2.

ЗАДАЧІ ВИБОРУ

2.1. Поняття бінарного відношення

2.2. Способи задавання відношень

2.3. Операції над відношеннями

2.4. Властивості відношень

2.5. Відношення еквівалентності, порядку, домінування та переваги

2.6. Поняття R-оптимальності, найкращого, найгіршого, максимального та мінімального елементів

2.7. Поняття функції вибору. Класи функцій вибору

2.8. Функції корисності

РОЗДІЛ 3

БАГАТОКРИТЕРІАЛЬНІ ЗАДАЧІ ОПТИМІЗАЦІЇ

3.1. Загальна постановка багатокритеріальної задачі оптимізації

3.2. Поняття ефективної альтернативи

3.3. Теоретичне і практичне значення ефективного рішення

3.4. Властивості ефективних альтернатив і способи їх знаходження

3.5. Загальна проблема пошуку компромісних рішень

3.5.1. Принципи рівномірності

3.5.2. Принципи справедливої поступки

3.5.3. Інші принципи оптимальності

3.6. Методи нормалізації критеріїв

3.7. Способи урахування пріоритету критеріїв

3.7.1. Методи урахування жорсткого пріоритету

3.7.2. Методи урахування гнучкого пріоритету

3.8. Методи розв’язання багатокритеріальних задач оптимізації

3.8.1. Методи зведення до узагальненого критерію (методи згортки)

3.8.2. Метод головного критерію

3.8.3. Метод послідовних поступок

2.1. Поняття бінарного відношення

Найпростіша ситуація, яка дозволяє зробити обґрунтований вибір з декількох об’єктів, виникає, коли подано один “критерій якості”, що дозволяє порівнювати будь-які два об'єкти, чітко вказати, який з них краще, й вибрати той (або ті) для якого цей критерій досягає максимального значення. Однак, в більшості реальних ситуацій, визначити один такий критерій доволі складно i взагалі не завжди можливо. Але для деяких пар об’єктів можна вказати, який з об’єктів пари краще. У таких випадках кажуть, що ці два об'єкти знаходяться у бінарному відношенні. Поняття бінарного відношення дозволяє формалізувати операції попарного порівняння i тому широко використовується у теорії прийняття рішень.

Тобто, говорити про відношення ми можемо лише тоді, коли ми вміємо виділяти множину об’єктів, на якій це відношення визначено. Математично визначення відношення можна сформулювати таким чином.

О з н а ч е н н я  2.1. Відношенням R на множині  називається підмножина множини 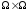, тобто

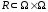
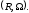Задавання підмножини R в множині визначає які пари знаходяться у відношенні R. Будемо позначати відношення R на множині  таким чином: Якщо елементи x та y множини  знаходяться у відношенні R , то це можна записати таким чином: або .

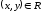2.2. Способи задавання відношень

Для того, щоб задати відношення 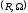необхідно задати всі пари 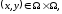які включено в R. Крім повного перелічування усіх пар існують три способи задавання відношень: задавання відношення матрицею, задавання графом та задавання відношення розрізами. Перші два способи застосовуються для задавання відношень на скінченних множинах, задавання відношення розрізами може бути застосовано і для нескінченних множин.

Опишемо ці способи задавання відношень.

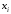2.2.1. Задавання відношення матрицею. Нехай  складається з n елементів, R – відношення на . Занумеруємо елементи множини  цілими числами від 1 до n. Для того, щоб задати відношення побудуємо квадратну таблицю розміром . Її i-ий рядок відповідає елементу множини , j-й стовпчик – елементу 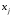з . На перерізі i-го рядка та j-го стовпчика ставимо 1, якщо виконується 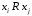, і нуль в інших випадках, тобто

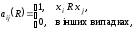
П р и к л а д  2.1. Нехай 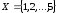, R відношення “більше” на множині Х. Тоді його можна задати матрицею таким чином:

2.2.2. Задавання відношення за допомогою графа. Для того, щоб задати відношення графом поставимо у взаємно однозначну відповідність елементам скінченної множини , на якій визначено відношення, вершини графа 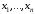(за будь-якою нумерацією).

Проведемо дугу від 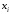, до , тоді й тільки тоді, коли виконується 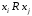(якщо i = j дуга 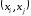перетворюється у петлю при вершині ).

Якщо задано будь-який орієнтований граф G з n вершинами, та вибрана нумерація на множині , то таким чином на  задане деяке відношення , таке, що виконується тоді і тільки тоді, коли в графі G є дуга 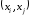. Отже, граф є геометричним зображенням відношення.

П р и к л а д  2.2. Задамо відношення з прикладу 2.1 графом.

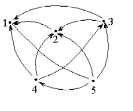
Рис. 2.1. Задавання відношення “більше” на множинi 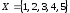за допомогою графа

2.2.3. Задавання відношень розрізами. Розглянемо відношення R на множині .

О з н а ч е н н я  2.2. Верхнім розрізом 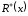відношення в елементі x називається множина елементів 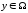таких, що

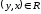
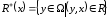. (2.1)

О з н а ч е н н я  2.3. Нижнім розрізом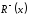 відношення в елементі х називається множина елементів 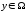таких, що

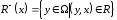. (2.2)

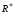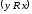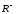Тобто верхній розріз (множина ) це множина всіх таких елементів y, які перебувають у відношенні R з фіксованим елементом х . Нижній розріз (множина ) – це множина всіх таких елементiв у, з якими фіксований елемент х знаходиться у відношенні R .

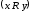Відношення R задане, якщо для кожного задано множину 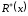або для кожного 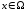задано множину .

П р и к л а д  2.3. Нехай 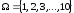, відношення R – «бути дільником», тобто , якщо х – дільник y. Задамо це відношення розрізами.

За допомогою верхніх розрізів:

, , , , ,

, , , .

Або за допомогою нижніх розрізів:

, , , , ,

, , , , .

Розглянемо відношення спеціального виду, та описані вище способи їх задавання.

Відношення називається порожнім (позначається ), якщо воно не виконується для жодної пари (x, y) Ì W´W .

Для порожнього відношення справедливо:

1. Матриця А () така, що a_i,j () = 0, для всіх i, j;

2. Граф G(Æ) не має дуг;

3. R⁺ (х) = 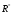(х) = Æ для всякого x  .

Відношення називається повним (позначається U), якщо воно виконується для всіх пар (x, y) Ì W´W. Для повного відношення вірно:

1. Матриця А (U) така, що a_i,j (U) = 1, для всіх i, j;

2. Граф G(U) такий, що дуги з’єднують аби-яку пару вершин;

3. Розрізи R⁺ (х) = 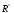(х) = W для всіх x  .

Відношення називається діагональним або відношенням рівності (позначається E), якщо воно виконується для всіх пар (x, y) Ì W´W, які складаються із співпадаючих елементів: x E y, якщо x та y це один і той самий елемент множини W. Для діагонального відношення Е мають місце твердження:

1. Матриця А (Е) така, що

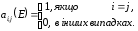
2. Граф G(Е) такий, що наявні тільки петлі у вершинах;

3. Розрізи R⁺ (х) = 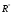(х) = x для всіх x  .

Відношення називається антидіагональним ( позначається 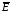), якщо воно виконується для всіх пар (x, y) Ì W´W, які складаються з не співпадаючих елементів. Для відношення справедливо:

1. Матриця А (Е) така, що

2. Граф G() такий, що наявні всі дуги (x_i , x_j ) якщо i  j, (відсутні тільки петлі при вершинах).

3. Розрізи R⁺ (х) = 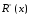=  \{x} для всіх x Î W.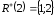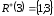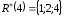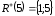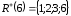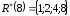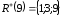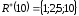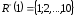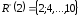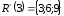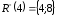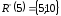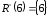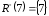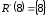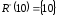