
- •От авторов
- •Лабораторная работа n 1. Определение плотности твердого тела
- •Раздел n 1. Законы сохранения в механике
- •Лабораторная работа n 11. Изучение закономерностей упругого и неупругого соударения тел
- •Лабораторная работа n 12. Измерение скорости полета пули с помощью баллистического маятника
- •Лабораторная работа n 13. Измерение скорости полета пули с помощью крутильного маятника
- •Раздел n 2. Динамика твердого тела.
- •Лабораторная работа n 21. Проверка уравнения вращательной динамики на приборе обербека
- •Лабораторная работа n 22. Определение момента инерции махового колеса способом колебаний
- •Лабораторная работа n 23. Определение момента инерции тела с помощью крутильного маятника
- •*Понятие тензора и эллипсоида инерции
- •Лабораторная работа n 26. Изучение свойств гироскопа
- •Лабораторная работа n 27. Маятник максвелла
- •Раздел n 3. Механика упругих тел
- •Лабораторная работа n 31. Изучение упругих деформаций
- •Раздел n 5. Механические колебания
- •Лабораторная работа n 51. Определение декремента затухания камертона
- •Лабораторная работа n 52. Определение частоты камертона способом биений
- •Лабораторная работа n 53. Изучение явления резонанса при вынужденных колебаниях пружинного маятника
- •Раздел n 6. Упругие волны.
- •Лабораторная работа n 61. Определение скорости звука в воздухе методом интерференции
- •Лабораторная работа n 62. Изучение колебаний однородной струны
- •Лабораторная работа n 63. Определение скорости звука в воздухе методом стоячей волны
- •Лабораторная работа n 64. Акустический эффект доплера
- •Приложение 1. Алгоритмы обработки результатов измерений
- •Приложение 2.
- •Приложение 3.
- •Содержание
Раздел n 6. Упругие волны.
Волнами называют возмущения среды, распространяющиеся в этой среде. Это понятие объединяет совершенно непохожие на первый взгляд явления: волны на поверхности воды, ударные волны, свет, звук и т.д.
Способность волн распространяться на значительные расстояния делает их удобным инструментом для исследования. Например, наблюдая за тем, как поглощаются в веществе световые волны можно делать вывод о химическом составе вещества, не разрушая образец. Другой пример - использование звукового эха (отраженной от препятствия звуковой волны) для измерения расстояний и скоростей движущихся тел.
Скорость волн в среде в значительной мере определяется свойствами самой среды и измерение скорости волн позволяет получать информацию об устройстве среды.
Предметом исследования механики являются волны в упругих средах. Здесь распространение возмущений обусловлено силами упругости, а конечность скорости волн - распределением массы по объему среды.
Цель описанных ниже работ состоит в исследовании характерных для упругих волн закономерностей и явлений, а так же в их использовании для получения информации о свойствах сред, в которых распространяются волны. Рассмотрение ограничивается случаем малых (удовлетворяющих принципу суперпозиции) возмущений. В этом случае согласно теореме Фурье задача сводится к исследованию гармонических волн, описываемых уравнением
![]() , (1)
, (1)
где A0(r) амплитуда волны, (tkr) фаза, начальная фаза, циклическая частота, k - волновой вектор, радиус-вектор r определяет координаты точки наблюдения относительно источника. Если сравнить аргументы функции синуса в выражениях (1) из предыдущего и данного разделов, можно сказать, что приведенная здесь формула описывает колебания, происходящие и в пространстве, и во времени. При этом модуль волнового вектора определяет максимальную быстроту изменения фазы в пространстве, а ориентация вектора k соответствует наиболее быстрому изменению фазы волны в пространстве. Направление вектора A0(r) определяется направлением смещения частиц в волне.
Волны, в которых k и A0(r) параллельны называют продольными, если k перпендикулярен A0(r), говорят о поперечных волнах. В газах и в толще жидкостей упругих поперечные волны не наблюдаются.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. "Самая первая" волновая поверхность, отделяющая пространство, в котором существует волновой процесс от того, в котором он еще не начался, называется волновым фронтом. Вектор k перпендикулярен волновым поверхностям. Расстояние между точками, колеблющимися с разностью фаз 2, отсчитываемое вдоль волнового вектора, называется длинной волны. Очевидно соотношение
![]() (2)
(2)
Вид волновых поверхностей определяется симметрией источника, т.е. некоторого тела, вызывающего вынужденные колебания в среде. По виду волновых поверхностей различают сферические (точечный источник), цилиндрические (линейный источник), плоские (источник в виде плоскости) и т.д. волны.
Ограничимся рассмотрением самых простых плоских волн. Простота в данном случае состоит в том, что волновой вектор k одинаков во всех точках пространства, и в абсолютно упругой (значит, не поглощающей волны) среде амплитуда плоской волны не зависит от координаты. Если направить ось X системы координат в направлении волнового вектора, то уравнение плоской поперечной волны будет выглядеть так
![]() . (3)
. (3)
Очевидно в этой волне смещения частиц среды происходят в направлении оси Y выбранной системы координат. Здесь легко понять смысл знака - перед k он соответствует перемещению фазы волны в положительном направлении оси X.
Выражение (3) является решением одномерного волнового уравнения
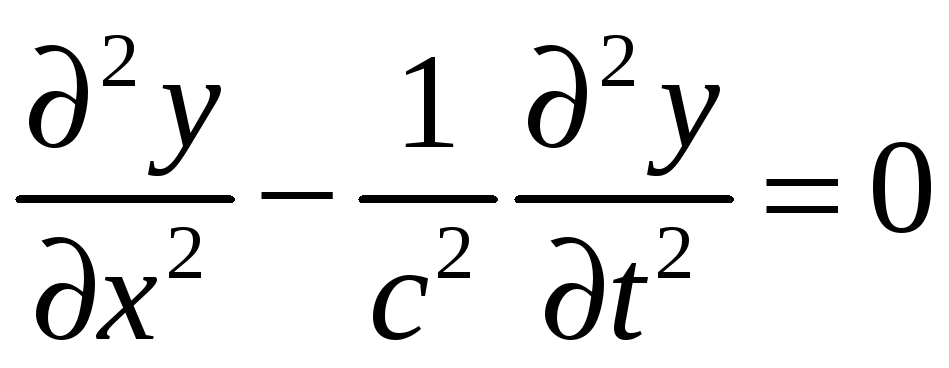 (4)
(4)
Единственный параметр этого уравнения с имеет размерность скорости и связан с частотой волны и волновым вектором соотношением
![]() (5)
(5)
где Т период колебаний. Отсюда очевидно, что c можно трактовать как фазовую скорость волны, т.е. отношение расстояния проходимого фазой за один период колебания, к величине периода колебания Т.
Важно отметить, что несмотря на математическую связь между k и c, они определяются совершенно различными физическими причинами. Циклическая частота волны задается исключительно источником колебаний, в то время как скорость c определяется природой волн (упругие, электромагнитные и т.д.) и соответствующими свойствами среды (упругими, электромагнитными и т.д.). Таким образом, независимые друг от друга величины и c определяют пространственную периодичность волны - величину вектора k.
ИНТЕРФЕРЕНЦИЯ ВОЛН
Явления интерференции и дифракции присущи исключительно волнам. С явлением дифракции обычно знакомятся на примере световых волн, здесь же описаны работы по изучению интерференции упругих волн.
Для простоты ограничимся случаем, когда две плоских волны с одинаковым направлением колебаний распространяются вдоль одной прямой. Если направить вдоль нее ось X системы координат, уравнения этих волн примут вид:
![]()
и (6)
![]() ,
,
где x01 и x02 - координаты источников волн. В моменты времени t01 и t02 в этих источниках достигаются максимальные значения смещений.
Как отмечалось ранее мы рассматриваем ситуации, когда выполняется принцип суперпозиции. Тогда результирующее смещение частиц среды y в точке наблюдения будет равно:
![]() . (7)
. (7)
Если бы фазы волн были одинаковы во всех точках пространства в любой момент времени, мы получили бы гармоническую волну с амплитудой y01y02, независящей от времени и пространственных координат.
Если же разница фаз
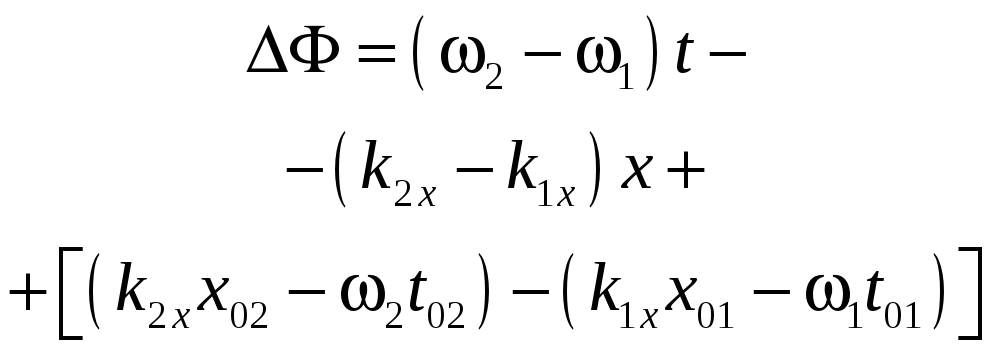 (8)
(8)
зависит от времени (в случае различных частот волн) или/и от координат (в случае различных волновых векторов), в разных точках пространства в разные моменты времени становятся возможными следующие ситуации:
-
y1 и y2 в выражении (7) имеют одинаковые знаки. В этом случае будет наблюдаться взаимное усиление волн, выражающееся в увеличении амплитуды колебаний по сравнению с y01 и y02.
-
y1 и y2 в выражении (7) имеют разные знаки. Здесь будет иметь место взаимное ослабление волн - амплитуда суммарного колебания станет меньше и y01 и y02.
В подобном перераспределении амплитуды в пространстве и во времени, в случае наложения нескольких различных волн суть явления интерференции. Очевидно, что изменения амплитуды суммарной волны наиболее заметны при y01 y02.
Выделяют два принципиально разных типа интерференции:
-
интерференцию волн с близкими частотами, идущих в одном направлении или биения.
-
интерференцию волн с одинаковыми частотами.
При рассмотрении особенностей этих типов интерференции будем полагать, что волны имеют одинаковые амплитуды y01 y02 a и равные нулю начальные фазы колебаний t01 t02 0. В этом случае уравнения волн примут вид
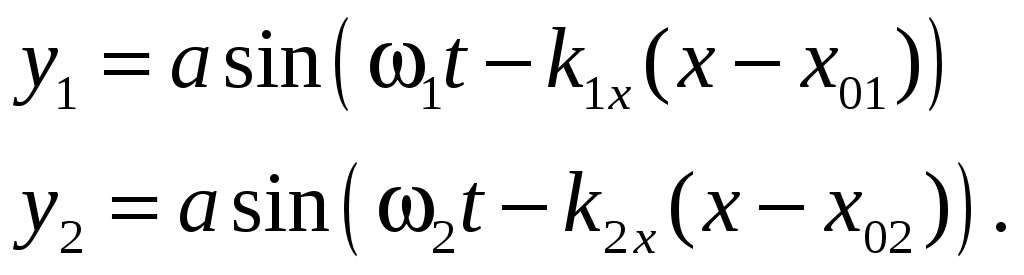 (9)
(9)
Уравнение суммарной волны просто получить пользуясь тригонометрическими формулами:
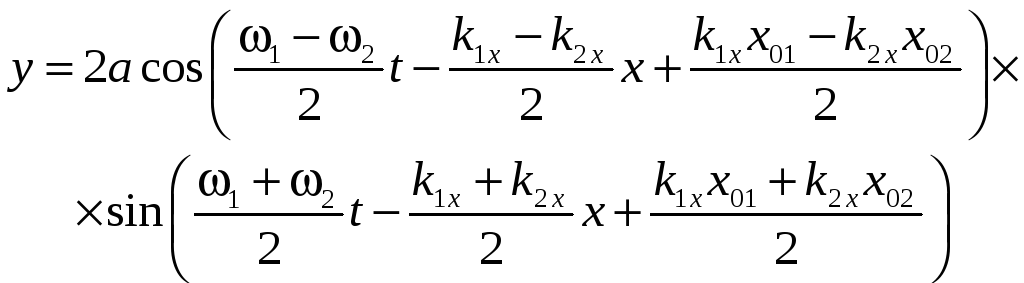 (10)
(10)
Роль амплитуды волны здесь играет функция
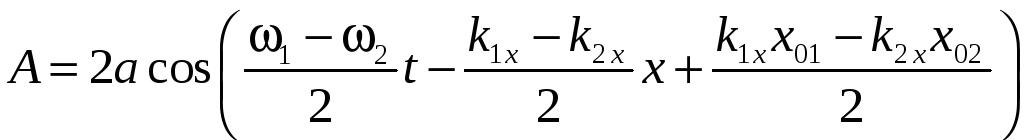 (11)
(11)
Биения
Наиболее простой вид для точки с координатой x 0 соотношения (10) и (11) принимают при k1x01 k2x02 кратных 2 (чего не ограничивая общности можно добиться соответствующим выбором системы отсчета)
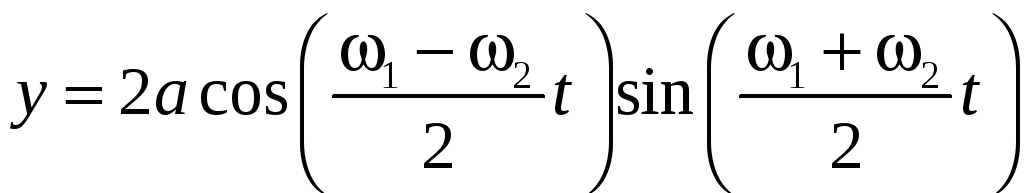 . (12)
. (12)
Функция (12) описывает колебание с частотой равной полусумме частот и и амплитудой меняющейся со временем:
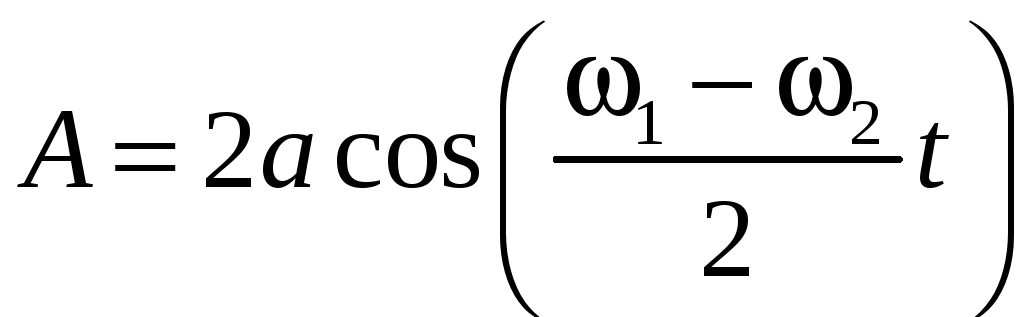 (13)
(13)
Рис. 1 Графики
функций (12) (сплошная линия) и (13) (штриховая
линия). 1/2
10.
При любом положении источников во всех точках пространства будут происходить колебания, подобные показанным на рисунке, только сдвинутые относительно их по фазе.
Подобные изменения амплитуды колебания со временем и называются биениями. Величину |1 2|, определяющую частоту изменения амплитуды называют циклической частотой биений.
Явление биений используется для измерения разницы близких частот волн (см. работу N 52).
Интерференция волн с одинаковыми частотами
При наложении двух плоских волн с одинаковыми частотами, волновыми векторами и амплитудами, распространяющихся вдоль одной прямой, выражения (10) и (11) сводятся к следующим:
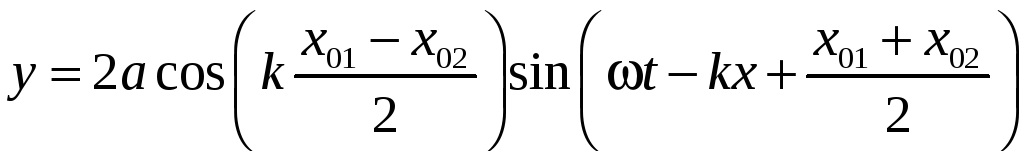 , (14)
, (14)
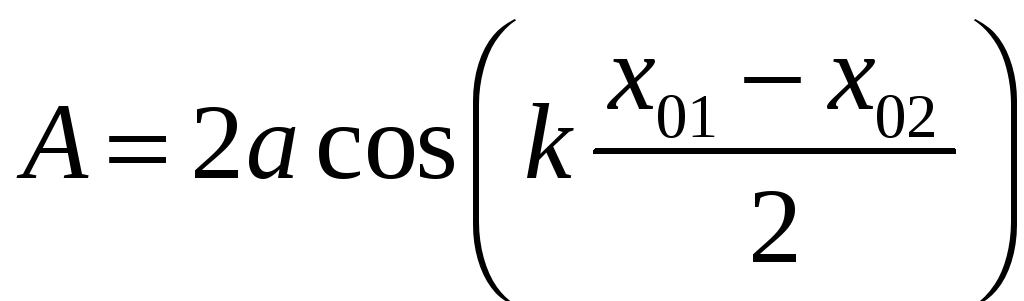 . (15)
. (15)
В этом случае амплитуда суммарной волны зависит только от разницы фаз kx k(x01 x02), которые волны набирают при распространении от своих источников до точки наблюдения. Так, если x равно целому числу волн
![]() , (16)
, (16)
колебания двух волн во всех точках пространства происходят в фазе, что приводит к их взаимному усилению.
Если же x равно не четному числу полуволн
![]() , (17)
, (17)
амплитуда суммарной волны рана нулю - колебания двух волн в точке наблюдения происходят в противофазе, что приводит к их взаимному гашению.
Стоячие волны
При интерференции волн с одинаковыми частотами особо интересен случай, когда две волны с одинаковыми амплитудами распространяются навстречу друг другу:
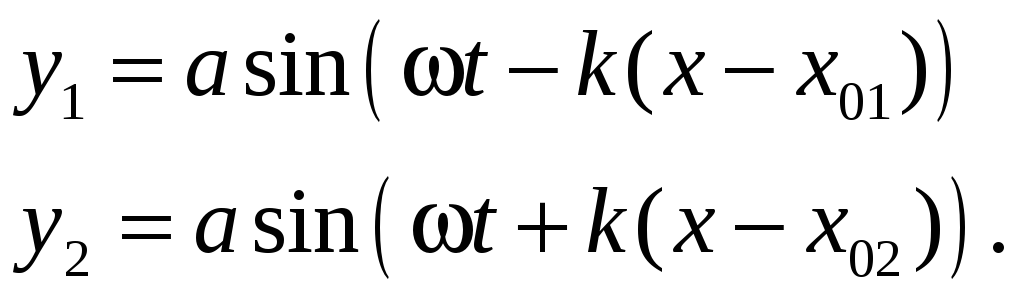
При этом, если поместить начало системы координат между источниками на равном от них удалении (x01 x02), то уравнение суммарной волны имеет максимально простой вид:
![]() . (18)
. (18)
Возбуждение среды, описываемое уравнением типа (18), называется стоячей волной. Происхождение этого термина понятно – уравнение (18) не описывает характерного для волн перемещения фазы колебания в пространстве. Амплитуда колебаний в стоячей волне зависит от координаты:
![]() (19)
(19)
Рис. 2 Вид стоячей
волны (18) для t
0 (сплошная линия) и t
T/2 (штриховая
линия). Стрелками показаны направления
смещений.
Длиной стоячей волны ст называется расстояние между ближайшими узлами. Очевидно, что ст= /2.
В связи с введением понятия стоячей волны уместно выделять волны бегущие, т.е. волны, в которых происходит перемещение фазы колебаний в пространстве. Бегущие волны описываются выражением (1).
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАЗДЕЛУ
-
*Познакомьтесь с описанием синусоидальных волн с помощью комплексных чисел. Освойте метод векторных диаграмм сложения колебаний. Получите с помощью этого метода выражение для суммы двух колебаний с разными частотами и разными фазами.
-
Объясните с точки зрения теории упругости, почему в газах и жидкостях отсутствуют поперечные волны.
-
*Пусть имеется полубесконечная абсолютно упругая среда. К плоской границе среды равномерно по площади приложена нормальная сила меняющаяся со временем по закону синуса достаточно долго. Запишите уравнение движения для единичного объема этой среды. Покажите, что для неоднородных квазистатических деформаций это уравнение имеет вид волнового уравнения (4), где фазовая скорость волны (в данном случае, очевидно, продольной) связана с модулем Юнга и плотностью среды выражением
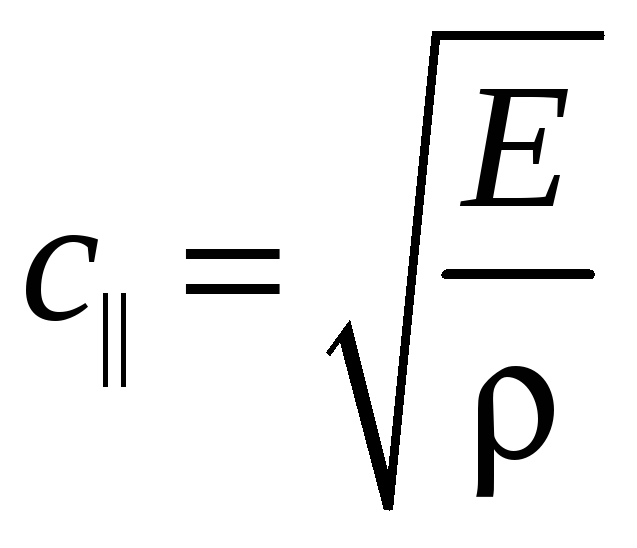 .
.
-
*Повторите рассуждения предыдущего задания для случая тангенциальной силы и получите для фазовой скорости поперечной волны соотношение
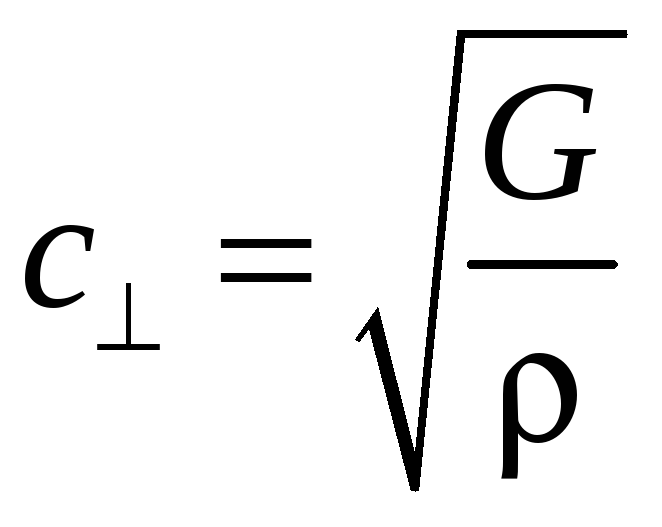 ,
,
где G - модуль сдвига.
-
На основании формул из двух предыдущих заданий и теории упругости сделайте вывод об относительных величинах фазовых скоростей продольной
 и
поперечных
и
поперечных
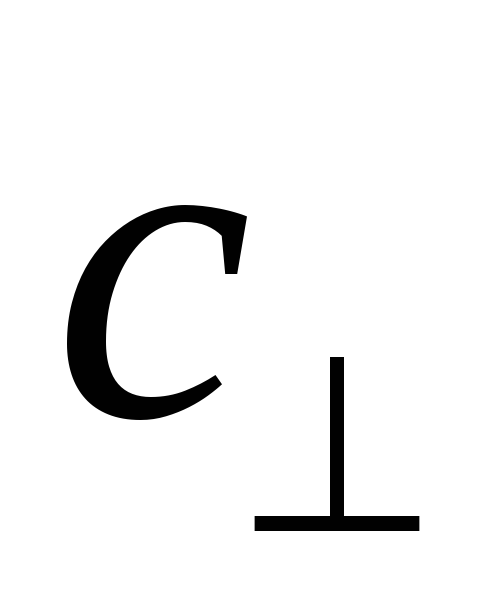 волн.
волн. -
Докажите, что в упругой среде, охваченной волновым процессом, существует избыток механической энергии, распределенной в пространстве с объемной плотностью
![]()
где a - амплитуда волны, - ее частота, - плотность среды.
-
В чем суть явления интерференции? Разберите случаи биений и интерференции волн с одинаковыми частотами1 .
-
Объясните, почему в выражении (10) роль амплитуды играет функция косинуса а не синуса.
-
Существуют ли условия при которых две волны во всех точках пространства усиливают (ослабляют) друг друга?
-
Приведите примеры возникновения стоячих волн в ситуациях из повседневной жизни.
-
*Рассмотрите наложение двух волн с одинаковыми частотами и амплитудами, волновые векторы которых направлены под углом и к оси X системы координат. Покажите, что в этом случае суммарное возбуждение среды может быть представлено как сумма стоячей и бегущей волн.
