Лабораторная работа n 31. Изучение упругих деформаций

Цель работы - экспериментальная проверка закона Гука, измерение модуля Юнга и модуля сдвига.

Рис.1.

Упражнение 1. Экспериментальная проверка закона Гука. Измерение модуля Юнга.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Приборы и принадлежности: исследуемая струна, закрепленная вертикально, два измерительных микроскопа, микрометр, измерительная линейка, набор гирь.

Принципиальная схема установки показана на рисунке 1. С помощью микроскопов 1 и 2 проводят измерение удлинения участка струны 3 между микроскопами. В качестве меток используются кусочки миллиметровой бумаги приклеенные к струне. Нагрузку можно менять, подвешивая к струне гири 4.

ХОД РАБОТЫ

1. Изучите правила работы с измерительными микроскопами, представленные в начале вводного раздела.

2. Добейтесь четкого изображения меток струны на фоне измерительных шкал микроскопов.

3. Снимите все гири со струны. Отметьте положение меток на струне по шкалам микроскопов.

4. Измерьте микрометром толщину струны d. Считая ее поперечное сечение кругом, рассчитайте его площадь S  d ²/4.

5. Измерьте линейкой расстояние l между метками на струне.

6. Нагрузите струну гирей и измерьте по шкалам микроскопов величины, на которые сдвинутся метки на струне. Относительное удлинение участка струны между микроскопами l можно найти по формуле

  l₂  l₁)/l

где l₁  изменение положения верхней метки, l₂  изменение положения нижней метки.

7. Найдите силу тяжести F  mg и определите коэффициент жесткости струны k = F/l = F/(l₂  l₁).

8. Определите нагрузку на единицу площади поперечного сечения струны f  F/S, где m  масса гири, g  ускорение свободного падения.

9. Повторите пункты 5 и 6 несколько раз для каждой из возможных нагрузок, проводя измерения  как при загрузке так и при разгрузке струны.

10. Постройте график зависимости (f). Выделите на графике линейный участок .

11. Определите модуль Юнга. Очевидно, (см. формулу (2)) что он будет равен тангенсу угла наклона линейного участка графика (f) к оси ординат.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К УПРАЖНЕНИЮ

1. В чем принципиальное отличие коэффициента жесткости и модуля Юнга?

2. Опишите цель эксперимента и способ ее реализации на конкретной экспериментальной установке.

3. Влияют ли на результаты эксперимента длина, толщина, масса струны?

4. С какой целью в работе используются два микроскопа?

5. Какие данные вашего эксперимента свидетельствуют о выполнении закона Гука?

6. Мысленно продолжите эксперимент, увеличивая нагрузку на струну. Как при этом поведет себя график (f)?

Упражнение 2. Измерение модуля сдвига способом крутильных колебаний.

Деформацию кручения можно классифицировать как неоднородный сдвиг. Поэтому имеется возможность определения модуля сдвига по периоду свободных колебаний крутильного маятника, в котором струна изготовлена из исследуемого материала.

Найдем связь между периодом колебаний крутильного маятника T и модулем сдвига материала струны. В работе 23 было показано, что период колебания крутильного маятника можно выразить через модуль кручения D и момент инерции I следующим образом

(7)

Модуль кручения D, по определению, связан с вращающим моментом M и углом , на который закручена струна соотношением

M  D 

Рис.2.

Установим эту связь на основе теории упругости. Разобьем струну на коаксиальные трубки с внутренним радиусом r и внешним радиусом rr. В такой трубе выделим параллелепипед шириной rd (см. рисунок 2) Из рисунка видно, что деформация, которую испытывает такой параллелепипед при кручении стержня, будет сдвигом. Запишем закон Гука для него:

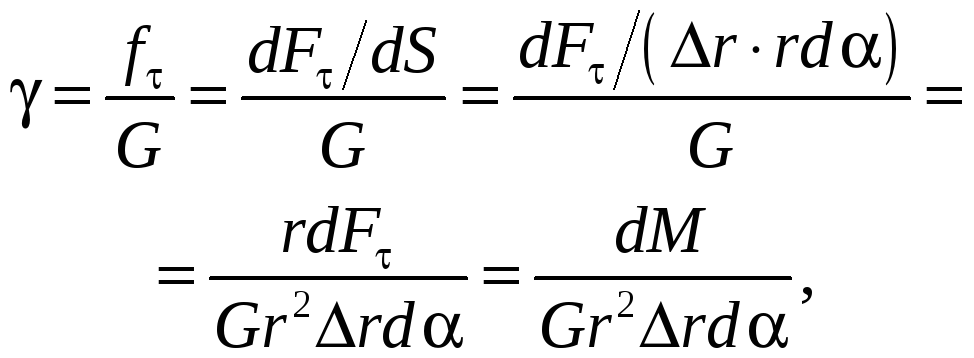(9)

где через dM обозначен момент силы dF_, действующей на основание выделенного параллелепипеда, dS  площадь этого основания. Из треугольника ABA' имеем: tgAA'/AB. Если углы  и  малы:   r/l. Подставив это выражение в формулу (9), получим:

.

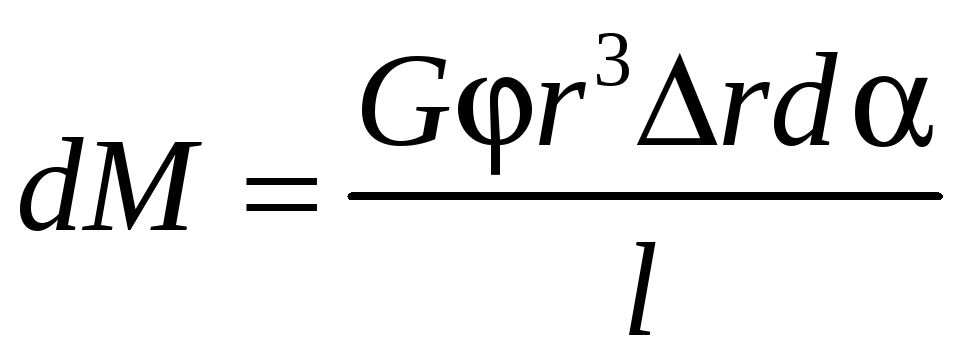Проинтегрировав это выражение по  от 0 до 2 и по r от 0 до R (радиус струны), получим:

.

Сопоставляя это выражение с формулой (8), найдем модуль кручения

.

С учетом соотношения (7) получим рабочую формулу:

. (10)

Итак, для измерения модуля сдвига струны крутильного маятника, необходимо измерить длину l и радиус R струны, момент инерции I и период собственных колебаний T крутильного маятника.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Приборы и принадлежности: исследуемая струна, закрепленная вертикально, груз с известным моментом инерции, секундомер, микрометр, измерительная линейка, весы.

В работе используется та же установка, что и в работе 23.

ХОД РАБОТЫ

1. Измерьте длину струны l линейкой, а ее радиус R  микрометром.

2. Момент инерции груза найдите по методу, описанному в работе 23. Если вы используете груз правильной геометрической формы, его момент инерции можно рассчитать по соответствующим формулам из таблицы 1 второго раздела, измерив необходимые геометрические параметры и определив массу взвешиванием.

3. Секундомером измерьте период свободных колебаний маятника.

4. По формуле (10) рассчитайте модуль сдвига. Оцените погрешность измерения.

5. Из формулы (5) выразите коэффициент Пуассона для материала струны и рассчитайте его, используя результаты этого и предыдущего упражнений.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К УПРАЖНЕНИЮ

1. В чем принципиальное отличие модуля кручения D и модуля сдвига G?

2. Опишите цель эксперимента и способ ее реализации на конкретной экспериментальной установке.

3. Воспроизведите самостоятельно вывод рабочей формулы (10).

4. Как влияют на точность эксперимента момент инерции маятника, длина и толщина струны?

5. Можно ли с помощью имеющихся в лаборатории приборов определить коэффициент Пуассона путем прямого измерения поперечных размеров струны?

**Упражнение 3. Измерение модуля Юнга из изгиба

Изгиб классифицируется как неоднородное растяжение-сжатие. Получим формулу, связывающую параметры изгиба и модуль Юнга.

Рассмотрим изгиб бруса (балки) произвольного сечения, постоянного по всей длине балки. Пусть до деформации брус имел прямолинейную форму (рис. 3). Мысленно проведя нормальные к оси бруса сечения AB и A'B', вырежем бесконечно малый элемент бруса ABA'B', длину которого обозначим через l₀. Ввиду малости последней можно считать, что в результате изгиба отрезки AA', BB', NN' и все отрезки параллельные им перейдут в дуги окружности с центром на некоторой оси O, перпендикулярной плоскости рисунка (см. рис. 3). Эта ось называется осью изгиба. Наружные волокна, лежащие выше линии NN', при изгибе удлиняются, волокна, лежащие ниже линии NN',  укорачиваются. Длина отрезка NN' остается неизменной. Линия NN' называется нейтральной линией. Проходящее через нее сечение (недеформированного) бруса плоскостью, перпендикулярной плоскости рисунка, называется нейтральным сечением. Пусть R  радиус кривизны нейтрального сечения (R  |NO|). Тогда l₀  R. Рассмотрим волокно бруса, находящееся на расстоянии  от нейтрального сечения. (0, если волокно выше нейтрального слоя, 0 , если  ниже.) Пусть брус не слишком толст, так что R. Тогда длина рассматриваемого волокна равна l   (R  ), а его удлинение l  l  l₀  . Такое удлинение сообщается нормальной к AB силой, величина которой в расчете на единицу площади сечения AB равна:

Рис. 3.

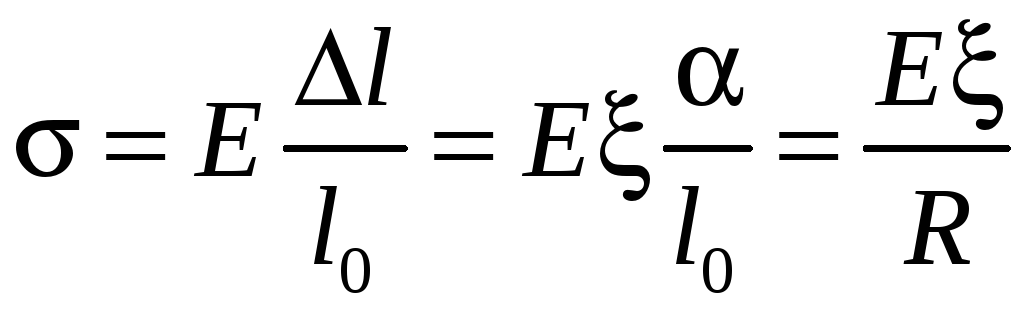. (11)

Будем считать, что мы имеем дело только с деформацией изгиба, т.е. сумма сжимающих и растягивающих сил, приложенных сечению AB равна нулю: , где dS - элемент площади рассматриваемого поперечного сечения бруса, интегрирование ведется по всему этому сечению. С учетом выражения (11) . Отсюда ясно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса (например, AB). Из следует, что момент сил M_, действующих на сечение AB, не зависит от того, относительно какой оси он берется. Для вычисления M_ проще всего взять ось, перпендикулярную плоскости рисунка и проходящую через точку N.

Очевидно, , (12)

или , (13)

где введено обозначение

. (14)

Величина I называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако в отличие от последней величины, имеющей размерность массы, умноженной на квадрат длины, I, определяемый выражением (14), имеет размерность четвертой степени длины.

Для бруса с поперечным сечением в виде прямоугольника с шириной a и высотой (AB) b легко получить

. (15)

Направим ось X вдоль нейтральной линии недеформированного бруса, ось Y  перпендикулярно X в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде y  y(x). По известной из математического анализа формуле

.

Если изгиб мал (y'), то квадратом производной можно пренебречь.

Тогда M_  EIy". (16)

Рис. 4.

Рассмотрим теперь балку, лежащую на двух опорах (см. рис. 4). Расстояние между опорами равно L. Пусть на балку действует вертикальная сила F. Вследствие симметрии сила F равномерно распределится между опорами. Расстояние между точками О и О' (положениями центра масс до и после изгиба) называется стрелой прогиба. Обозначим ее через z. Поместим начало координат в точку A, направим ось X вправо, а Y  вниз. Отсечем мысленно часть балки, проведя нормальное сечение через произвольную точку С(x) (с координатой x L/2). Справа на отсеченную часть балки будет действовать сила F/2, направленная вниз. Момент внешних сил, действующих на отсеченную часть, будет M = (F/2)x. Условие равновесия моментов принимает вид

. (17)

Знак минус в правой части обусловлен выбором системы координат: функция y(x), описывающая положение нейтральной линии, замедленно растет при x < L/2. Интегрируя уравнение (17) с учетом того, что y'(L/2) = 0 и y(0) = 0, найдем

. (18)

Тогда с учетом (15) получим стрелу прогиба для балки прямоугольного сечения

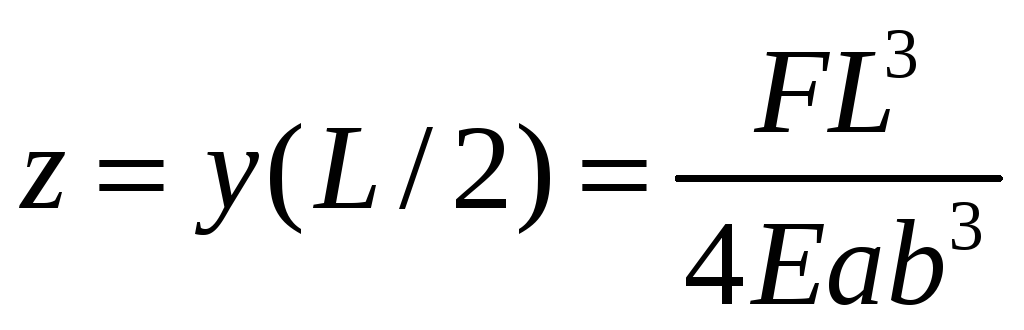. (19)

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Приборы и принадлежности: измерительная линейка, индикатор малых перемещений (индикатор), штангенциркуль, набор гирь, исследуемые балки, опоры.

Экспериментальная установка схематично изображена на рисунке 5. Прогиб балки 1, лежащей на опорах 2, создается весом гири 3. Стрела прогиба измеряется индикатором 4, укрепленным на подставке 5 с винтами 7. Вертикальное положение индикатора можно изменять винтом 6.

Рис. 5.

Из выражения (19) легко получить рабочую формулу:

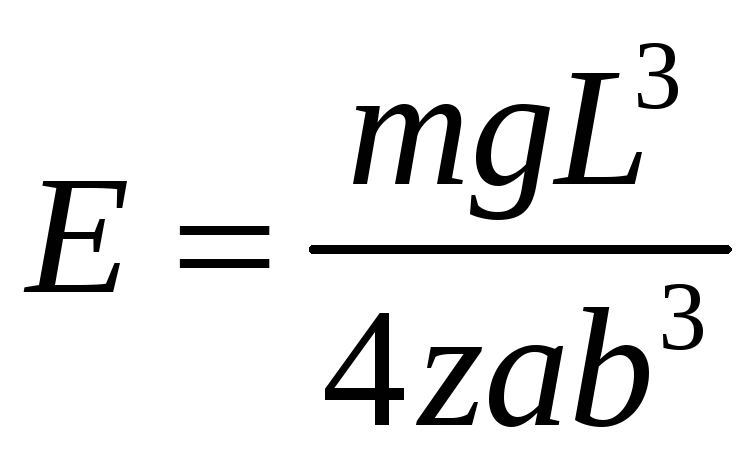, (20)

где m  масса гири, g  ускорение свободного падения.

ХОД РАБОТЫ

1. Установите опору 5 горизонтально (см. рис. 5), вращая винты 7.

2. Измерьте линейкой расстояние L между вершинами опор 2, а штангенциркулем толщину b и ширину a балки.

3. Положите балку на опоры. Вращая винт 6 (см. рис. 5), поднимите индикатор до касания с нижней поверхность балки. Поверните обод индикатора, чтобы положение стрелки совпало с нулем шкалы. Слегка постукивая по столу добейтесь устойчивого положения стрелки индикатора.

4. Положите гирю на балку. Слегка постукивая по столу добейтесь устойчивого положения стрелки индикатора, и определите по нему стрелу прогиба z.

5. Повторите измерения z несколько раз, меняя поворотом верхнюю и нижнюю стороны балки местами. Рассчитайте модуль Юнга по формуле (20).

6. Эксперимент повторите для всех имеющихся в распоряжении балок.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К УПРАЖНЕНИЮ

1. Изучите теорию изгиба, получите рабочую формулу.

2. **Проанализируйте, какой из двух методов измерения модуля Юнга, описанных в упражнениях 1 и 3, точнее теоретически? Сравните точности измерений модуля Юнга, полученные в ходе выполнения упражнений 1 и 2. Объясните результат сравнения.

3. Проведите сравнительный анализ измеренных модулей Юнга для разных материалов.

4. Если положить балку на опоры без гири, она все равно прогнется под действием собственного веса. Как это обстоятельство влияет на измерение стрелы прогиба и модуля Юнга?

5. В целях минимизации ошибки малые величины, входящие в знаменатели дробей, необходимо измерять как можно точнее. Почему же на ваш взгляд в этой работе для измерения толщины и ширины бруса рекомендуется штангенциркуль, а не микрометр?

РАЗДЕЛ N 4.

ЗЕМНОЕ ТЯГОТЕНИЕ

Ускорением свободного падения g называется ускорение относительно Земли, c которым свободное тело начинает падать. Это ускорение определяется суммой силы гравитационного притяжения Земли и центробежной силы инерции.

ЛАБОРАТОРНАЯ РАБОТА N 41.

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

(ОБОРОТНЫЙ И СЕКУНДНЫЙ МАЯТНИКИ)

Для определения ускорения g можно воспользоваться физическим маятником. Физическим маятником называется абсолютно твердое тело, которое может качаться вокруг неподвижной горизонтальной оси. При отсутствии силы трения уравнение движения маятника выглядит следующим образом:

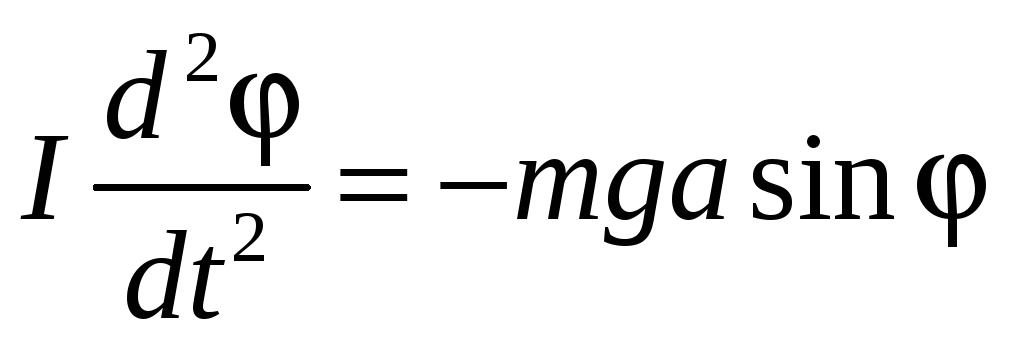, (1)

где m - масса тела, I - момент инерции относительно точки подвеса, a - расстояние от точки подвеса до центра тяжести,  - угол отклонения маятника от положения равновесия. В случае малых колебаний в этом уравнении можно заменить sin  на . В результате получим уравнение гармонического колебания с периодом:

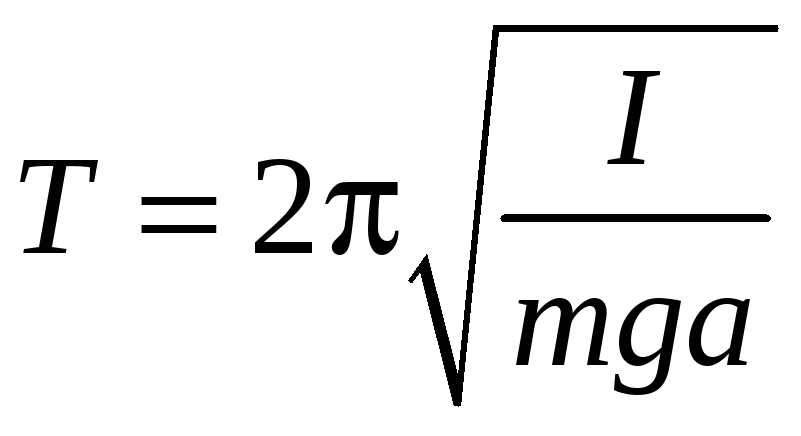(2)

Частным случаем физического маятника является математический маятник. Так называется гипотетический маятник, вся масса которого сосредоточена в одной точке. В этом случае формула (2) упрощается (так как I  ml² ,a  l, где l- длина маятника) и для ускорения свободного падения получим:

(3)

Отсюда ясна идея одного из способов определения ускорения свободного падения. Необходимо измерить длину и период математического маятника.

Сравнивая формулы (2) и (3), приходим к выводу, что физический маятник колеблется так же, как математический с длинной . Эта величина называется приведенной длинной физического маятника. Точка, удаленная от точки подвеса на расстояние l вдоль прямой, проходящей через центр масс, называется центром качания. Если маятник подвесить за центр качания, то период его колебаний не изменится (теорема Гюйгенса).

Важно иметь ввиду, что тот же самый период колебаний маятника может получиться при закреплении его, вообще говоря, в бесконечном множестве точек. Такие точки называются точками взаимности. Исходя из этого определения, центр качания и точка подвеса являются точками взаимности, но не единственно возможными. Поэтому расстояние между точками взаимности, которые легко установить по совпадению периодов колебаний, не всегда совпадает с приведенной длиной. Расстояние между точками взаимности равно приведенной длине физического маятника, только в том случае, если эти точки лежат на одной прямой с центром масс на разных расстояниях от него.

Упражнение 1. Оборотный маятник

Рис. 1

Оборотный маятник  устройство для определения ускорения свободного падения. Он состоит из стального стержня, на котором жестко закреплены опорные стальные призмы П₁ и П₂ и стальная чечевица А, находящаяся между ними (рис.1). Другая стальная чечевица В находится на одном из концов стержня (не между призмами), она может перемещаться по стержню и закрепляться в нужном положении. Перемещением этой чечевицы достигают совпадения периодов колебаний маятника, когда точками подвеса являются ребра опорных призм П₁ и П₂. В этом случае ребра призм будут точками взаимности. Эти ребра закреплены асимметрично относительно центра масс С. Поэтому при совпадении периодов колебаний расстояние между ними дает приведенную длину физического маятника l. Измерив период его колебаний T, можно вычислить g по формуле (3).

ХОД РАБОТЫ

1. Линейкой измерьте расстояние l между призмами.

2. Подвесьте маятник на одну из призм. Отклоните маятник на небольшой угол.

3. Отсчитайте как можно больше полных колебаний и определите по секундомеру время t, за которое они совершаются, рассчитайте период колебания T₁.

4. Подвесьте маятник на другую призму и найдите период T₂.

5. Найдите периоды колебаний T₁ и T₂ для 7 положений чечевицы В.

6. На одном поле координат постройте графики зависимости периодов колебаний T₁ и T₂ от положения чечевицы.

7. Найдите точку пересечения графиков, определите период колебания в точке взаимности T = T₁ = T₂.

8. Рассчитайте g по формуле (3).

Упражнение 2. Секундный маятник.

Для измерения ускорения свободного падения можно использовать математический маятник, хорошим приближением к которому является массивный шарик на длинной по сравнению с его радиусом нити.

Для точного измерения периода колебаний маятника используется способ биений (см. работу N 52). В качестве эталонной частоты выбирается частота колебаний секундного маятника, период которого составляет T_c  2с.

ХОД РАБОТЫ

1. Наматывая нить математического маятника на кронштейн, добейтесь, чтобы длина маятника была немного меньше 1 метра.

2. Отклоните оба маятника в одну сторону и одновременно отпустите их. Сосчитайте количество колебаний n секундного маятника, через которое маятники опять будут двигаться синхронно.

3. Найдите период колебаний математического маятника по формуле .

4. Вычислите g по формуле (3).

5. Увеличьте длину математического маятника до величины, немного превышающей 1 м.

6. Повторите пункты 24.

7. Найдите среднее значение g.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАБОТЕ

1. Что такое силы инерции?

2. Сформулируйте закон всемирного тяготения Ньютона.

3. Запишите уравнения движения материальной точки во вращающейся земной системе отсчета. Оцените величины входящих в него сил.

4. Что такое сила тяжести? Что такое ускорение свободного падения?

5. Оцените вклад в ускорение свободного падения центробежной силы Земли.

6. Что такое вес тела?

7. Какие проблемы возникают при определении массы тела путем взвешивания?

8. Докажите теорему Гюйгенса.

9. Опишите методы определения ускорения свободного падения, использованные в работе. Получите рабочие формулы. Какие допущения при этом используются и как они учтены в конструкции экспериментальных установок?

10. Получите формулу для периода колебаний, используемую в упражнении с секундным маятником.

11. Каковы преимущества использования секундного маятника по сравнению с секундомером?

12. В чем преимущества и недостатки методов измерения ускорения свободного падения с помощью оборотного и секундного маятников?