
- •1. Комплексные числа (кч)
- •Комплексная плоскость.
- •Введение в математический анализ.
- •Счетное множество – это множество, элементы которого можно посчитать.
- •Кванторы
- •Функции делятся на 2 класса
- •Элементарные неэлементарные
- •П римеры:
- •Используем бином Ньютона для доказательства неравенства:
- •Тогда .
- •Пусть функция определенна в окрестности точки .
- •Производная параметрически заданной функции.
- •Теорема Рояля, теорема о корнях производных.
- •Пусть и гладкие в окрестности и
- •Треугольник Паскаля.
- •Монотонность.
- •Если в критической точке 2-ая производная больше нуля, то это точка минимума, а если в критической точке 2-ая производная меньше нуля, то это точка максимума.
- •Асимптоты
Производная параметрически заданной функции.
Примеры параметрических функций:
1)
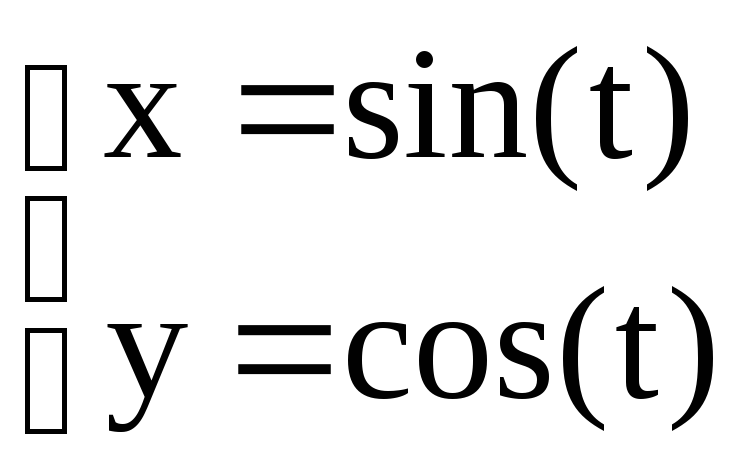
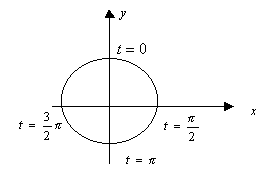
2)
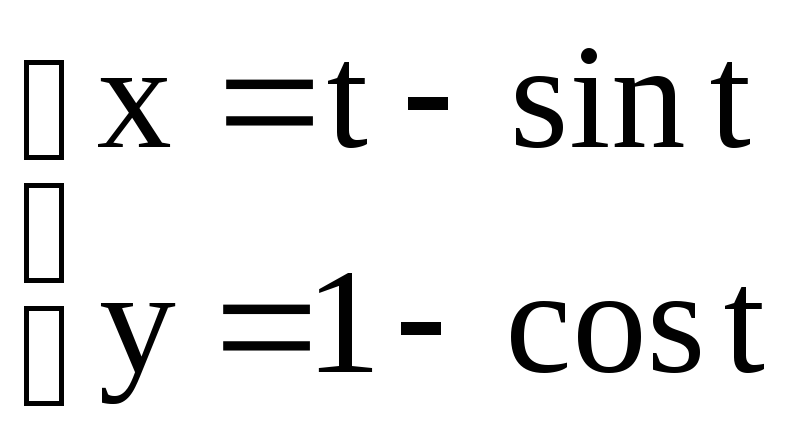
3 )
)
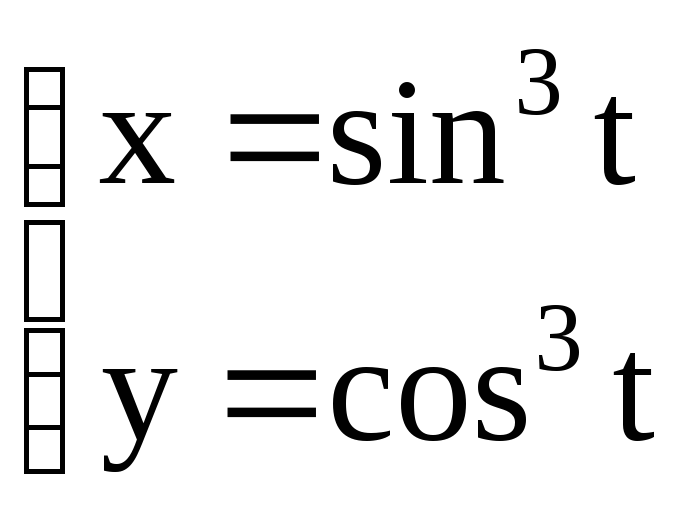
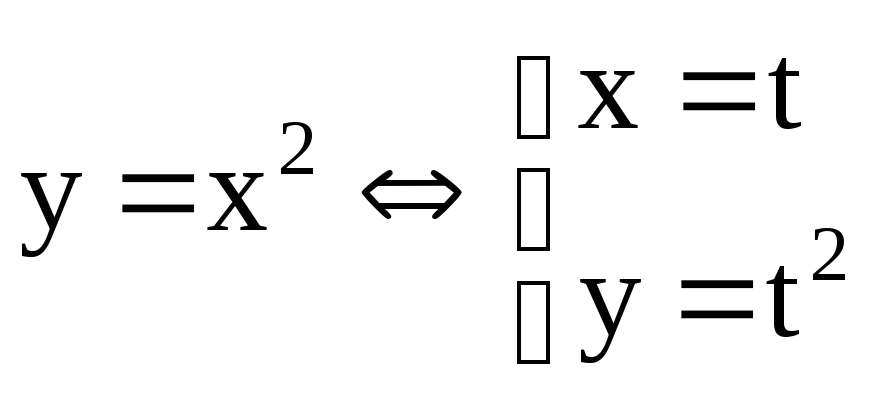
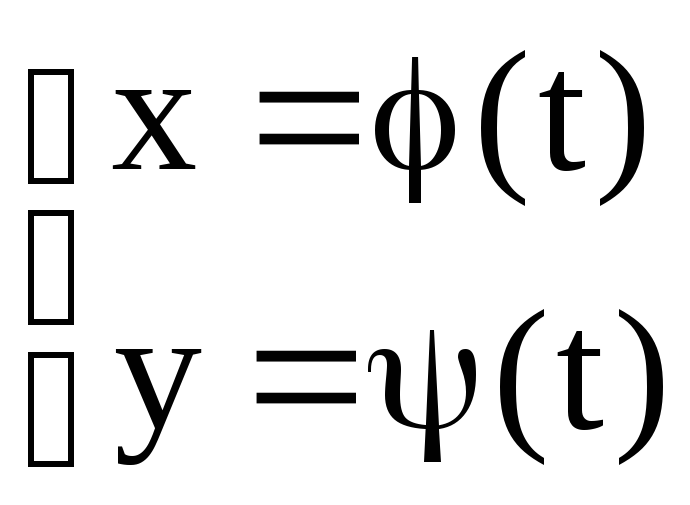
![]() – дифференцируемы.
– дифференцируемы.
![]()
Пример:
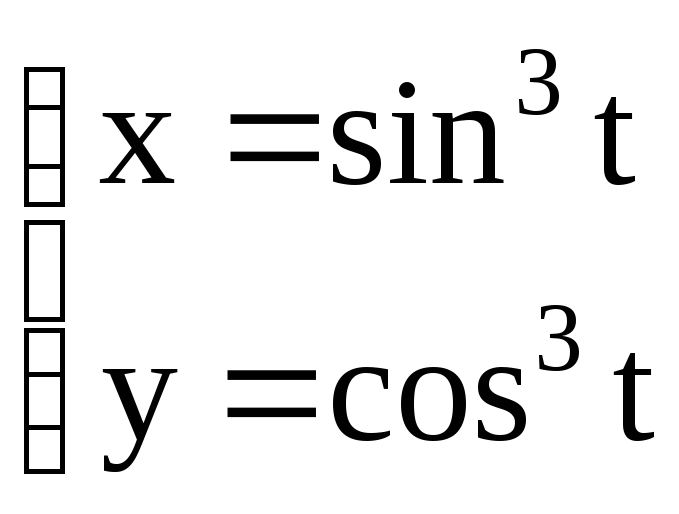
![]()
![]()
Гиперболические функции.
![]() (гипер. синус)
(гипер. синус)
![]() (гипер. косинус)
(гипер. косинус)
![]() (гипер. тангенс)
(гипер. тангенс)
![]() (гипер.
котангенс)
(гипер.
котангенс)
arsh (ареа синус)
arсh (ареа косинус)
arth (ареа тангенс)
arcth (ареа котангенс)
![]()
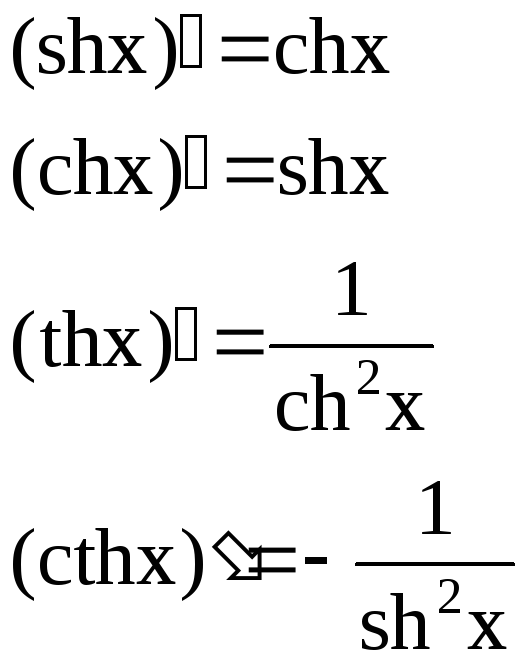
Схематичные графики гиперболических функций:
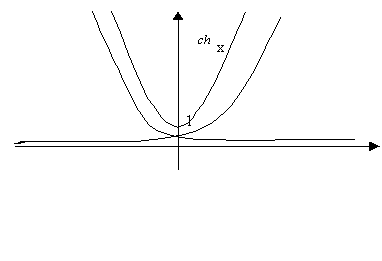
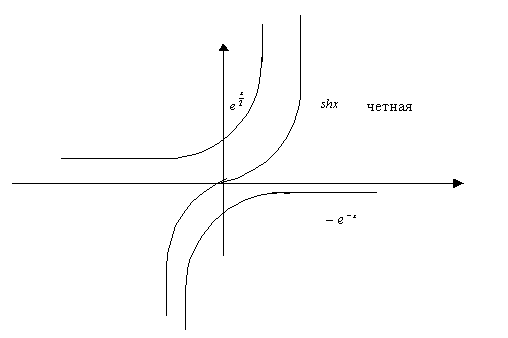

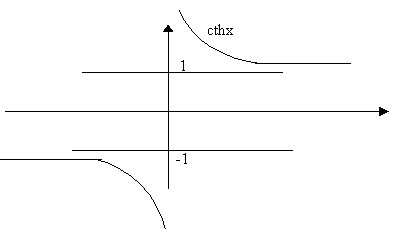
Производные высших порядков.
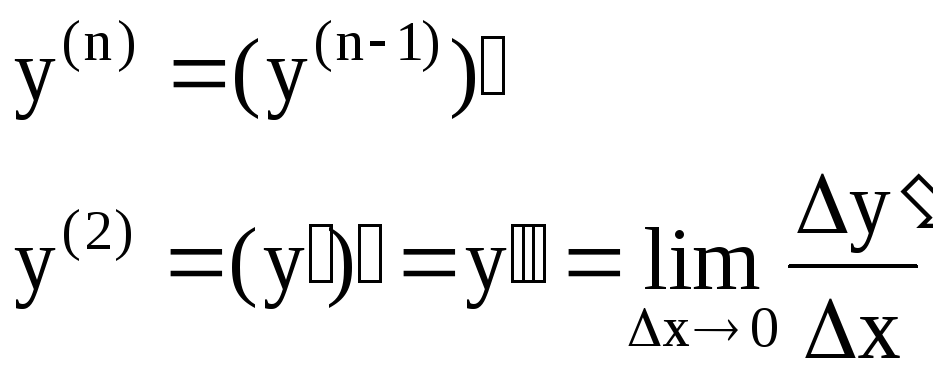
Механический смысл второй производной – это ускорение.
Геометрический смысл второй производной – отвечает за вогнутость или выпуклость графика функции.
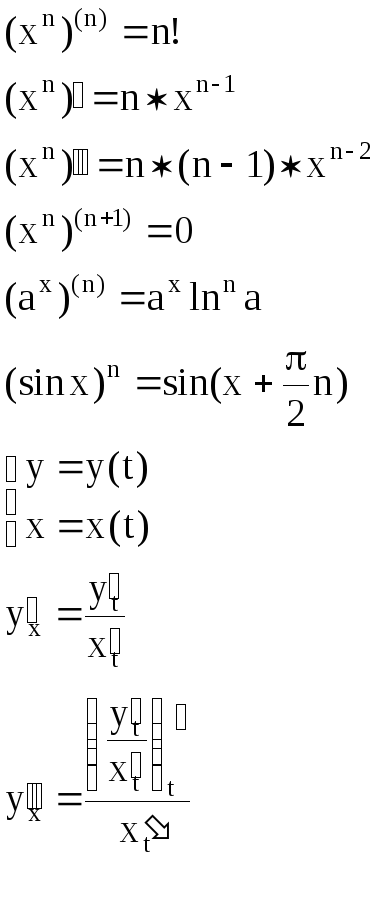
Дифференциал.
![]() – гладкая,
непрерывная и дифференцируемая.
– гладкая,
непрерывная и дифференцируемая.
![]()
![]()
![]()
Дифференциалом называется главная (линейная) часть приращения функции.
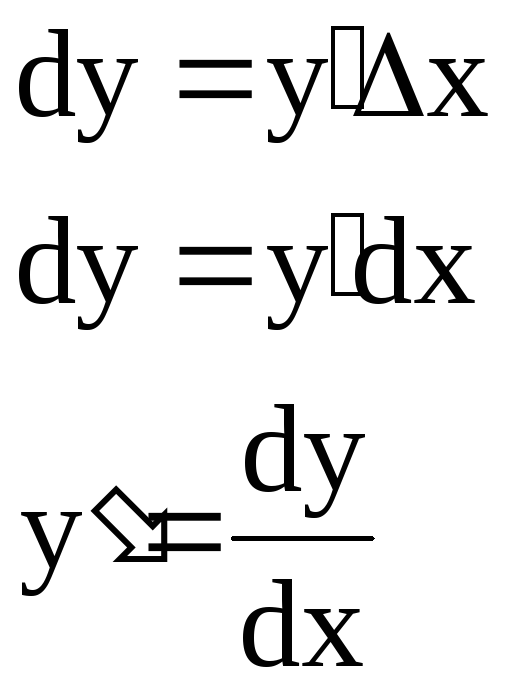 если
если
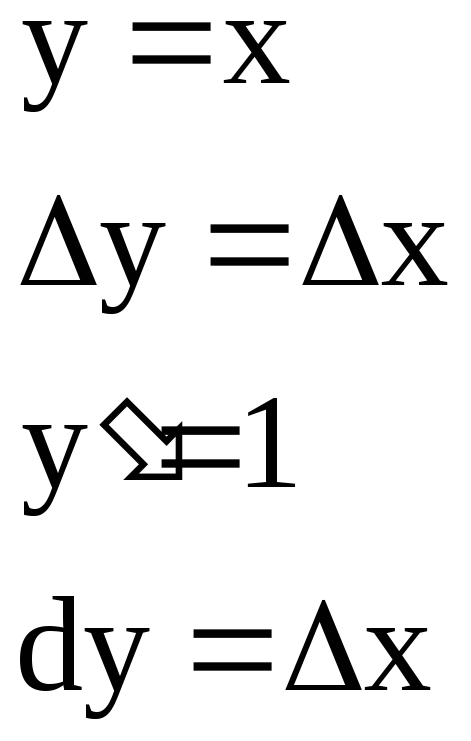
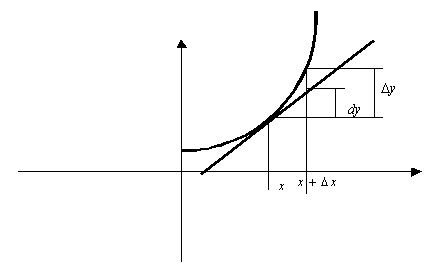
Свойства дифференциала:
1)![]()
2)![]()
3)![]()
4)![]()
Доказательство
для
![]() :
:
![]()
Остальные доказываются аналогично.
Инвариантность формы дифференцирования.
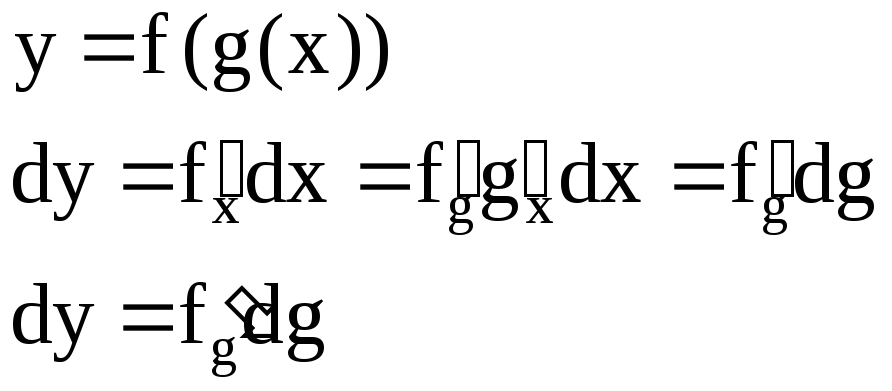
![]()
Форма дифференциала функции (производная умножить на дифференциал аргумента), не зависит от того, является ли аргумент функции независимой переменной или функций другого аргумента.
Основные теоремы дифференциального исчисления.
Теорема Рояля, теорема о корнях производных.
Доказательство:
Пусть
![]() гладкая
на
гладкая
на![]() ,
,![]()
![]() .
.
Тогда
![]()
![]()
![]()
![]() :
:
![]()
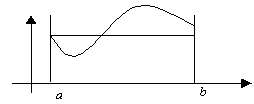
Любая гладкая функция, имеющая на концах отрезка одинаковые значения имеет, внутри этого отрезка, хотя бы один корень производной.
![]()
![]() при
при
![]()
![]()
![]() при
при
![]()
![]()
![]()
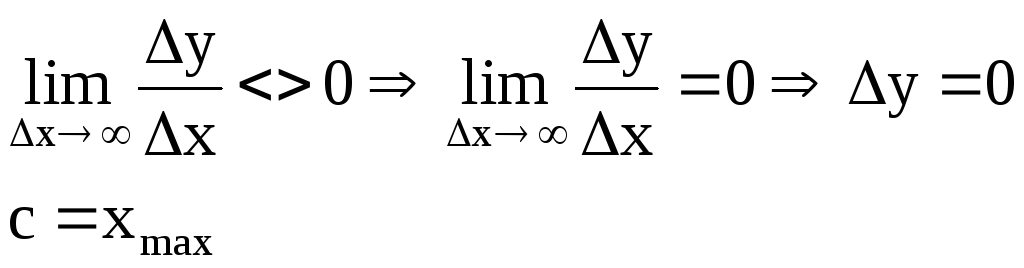
![]()
Теорема Каши о среднем.
Доказательство:
Пусть
![]() - гладкие на
- гладкие на
![]() .
.
![]() на
на
![]()
Тогда![]()
![]()
![]() :
:![]() , где
, где
![]() .
.
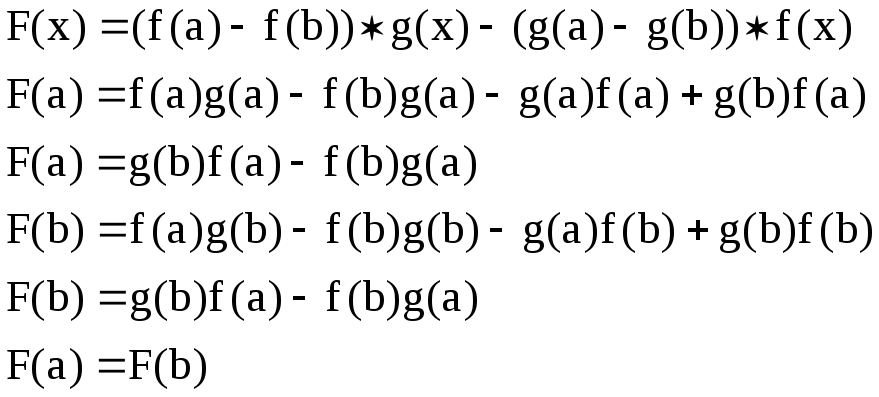
F
– гладкая
на отрезке
![]() .
По теореме Роле
.
По теореме Роле
![]()
![]() :
:
![]() .
.
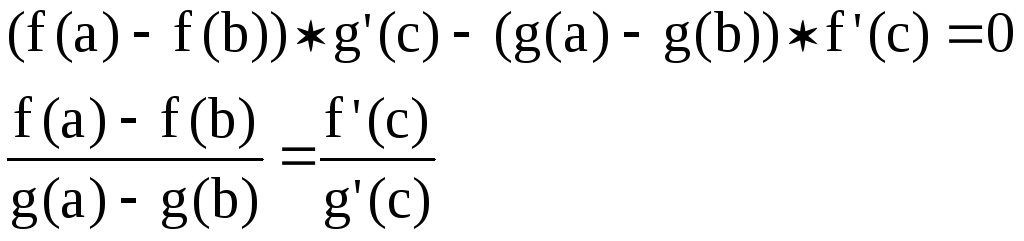
![]() по условию, а
по условию, а
![]() так как иначе по теореме Рояля
так как иначе по теореме Рояля
![]() ,
что противоречит условию.
,
что противоречит условию.
Теорема Логранжа. Теорема о конечных приращениях.
Доказательство:
Пусть
![]() гладкая
на
гладкая
на![]() ,
,
Тогда
![]()
![]()
![]()
![]() :
:
![]() .
.
Пусть
![]() :
:
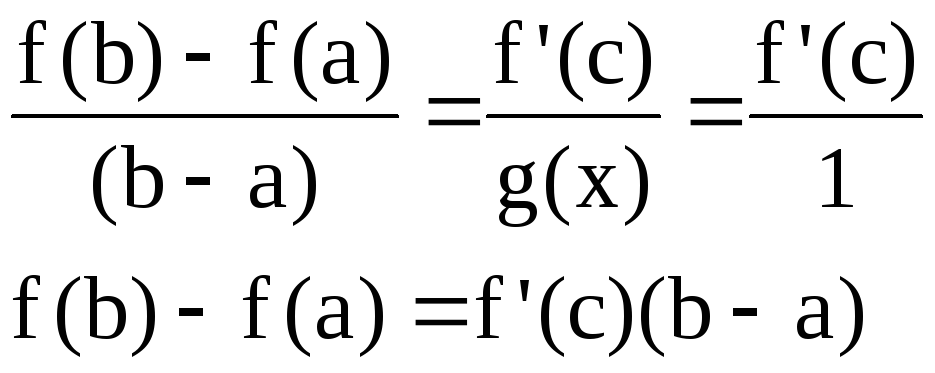
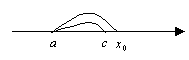
Г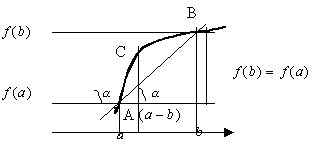 еометрический
смысл:
еометрический
смысл:
Для любой гладкой на замкнутом отрезке кривой найдется точка, в которой касательная параллельна хорде AB.
![]()
Правило Лопиталя (теорема Вернули – Лопиталя).
Пусть и гладкие в окрестности и
Тогда
![]()
![]()
Правило Лопиталя: Придел отношения функций равен приделу отношения их производных.
Доказательство:
Применим теорему
для
![]() и
и
![]() ,
,
![]() ,
где
,
где
![]() точка в окрестности
точка в окрестности
![]() .
.
![]()
где
![]() .
.
![]()
![]()
![]()
Примеры:
1)![]()
![]()
2)![]()
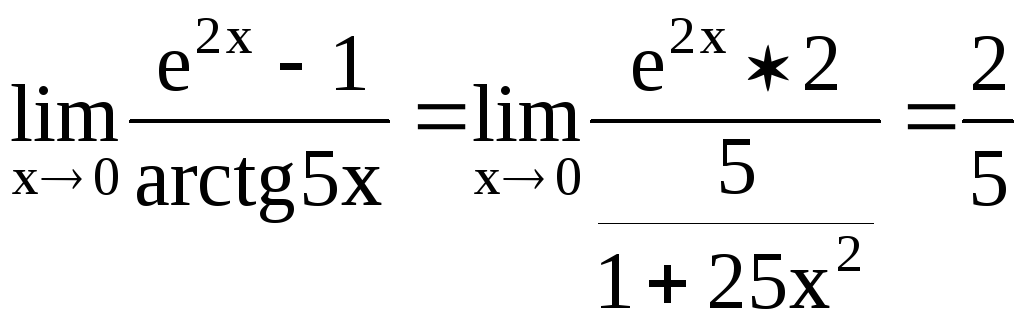
3)![]()
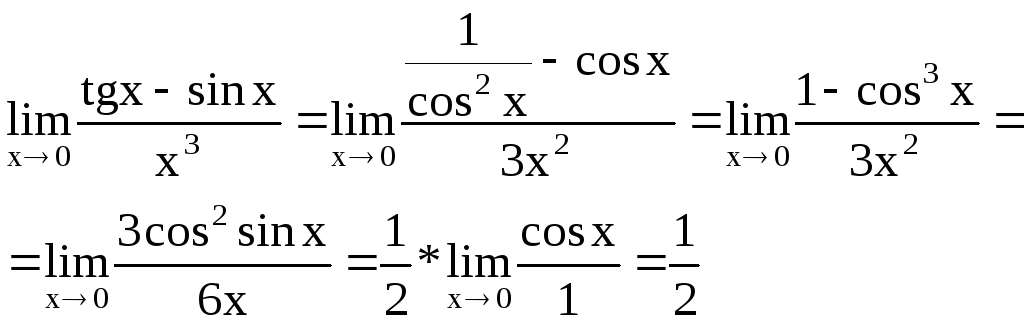
Формула Тейлора.
Пусть
![]() определена
и непрерывна и имеет все производные
до n-ого
порядка включительно, в некоторой точке
определена
и непрерывна и имеет все производные
до n-ого
порядка включительно, в некоторой точке
![]() .
.
![]()
![]() -
остаточный член в форме Тейлора.
-
остаточный член в форме Тейлора.
![]() -
полином Тейлора для
-
полином Тейлора для
![]() .
.
![]()
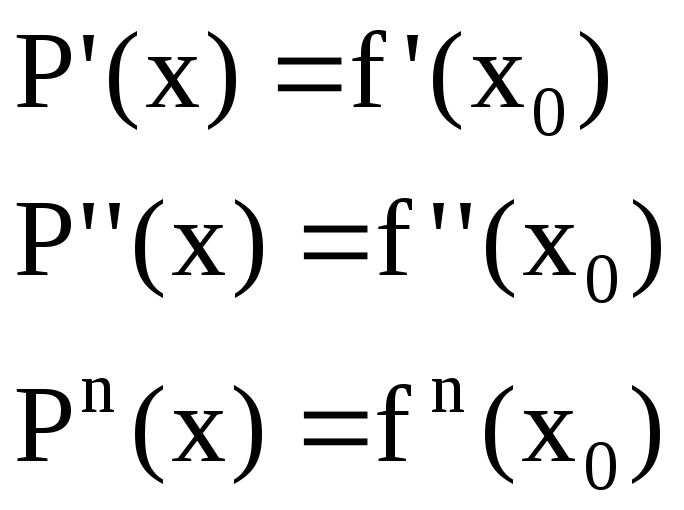
1)
![]()
2)
![]()
3)
![]() ,
где
k=0,1,2,…n.
,
где
k=0,1,2,…n.
Запись остаточного члена.
![]()
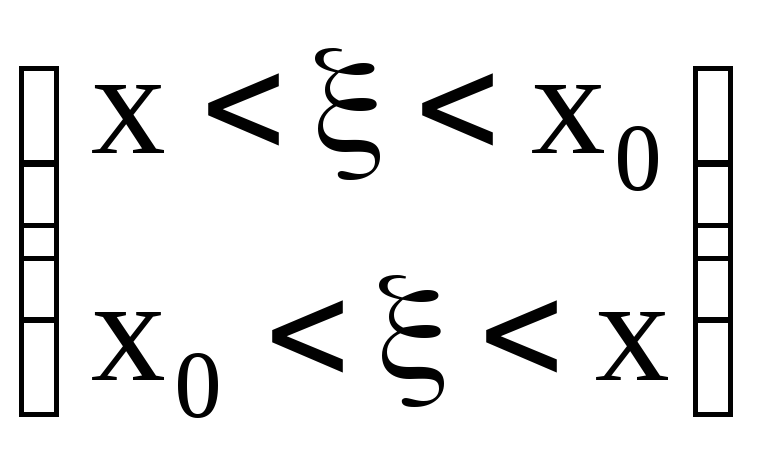 – остаточный член
в форме Логранжа.
– остаточный член
в форме Логранжа.
![]() – остаточный член
в форме Каши.
– остаточный член
в форме Каши.
![]() – остаточный член
в форме Пиано.
– остаточный член
в форме Пиано.
Ряд Тейлора.
![]()
Формула Маклорена.
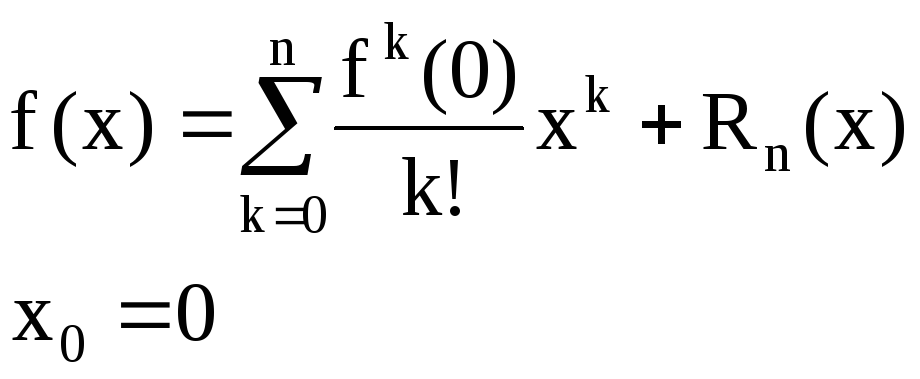
Любой многочлен совпадает со свой формулой Маклорена, при этом постоянный член равен 0.
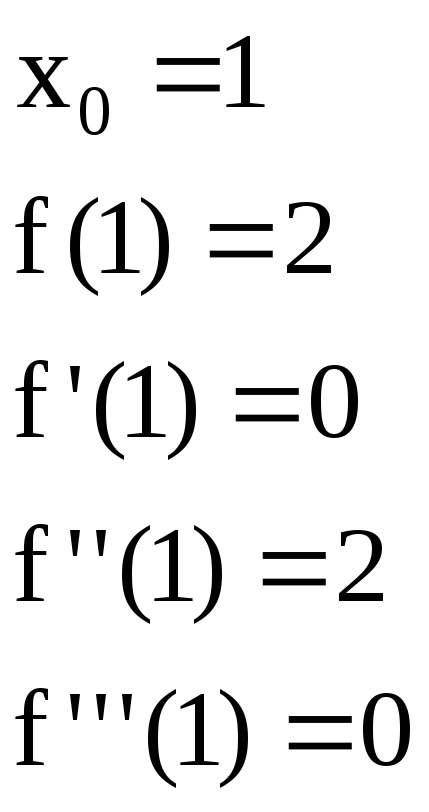
![]()
2)
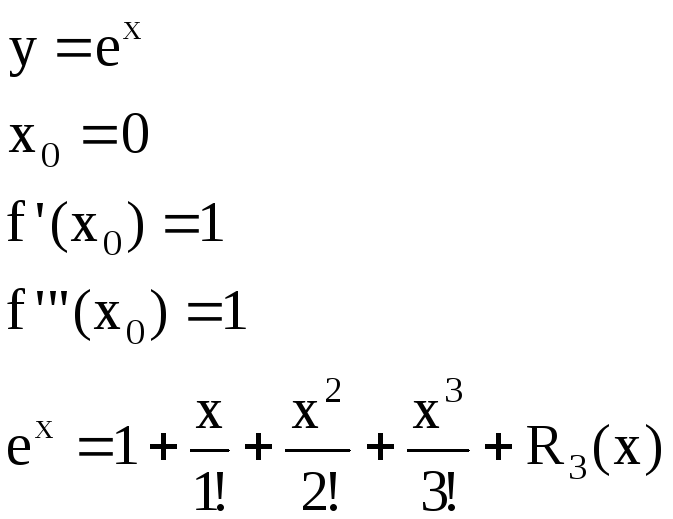
3)
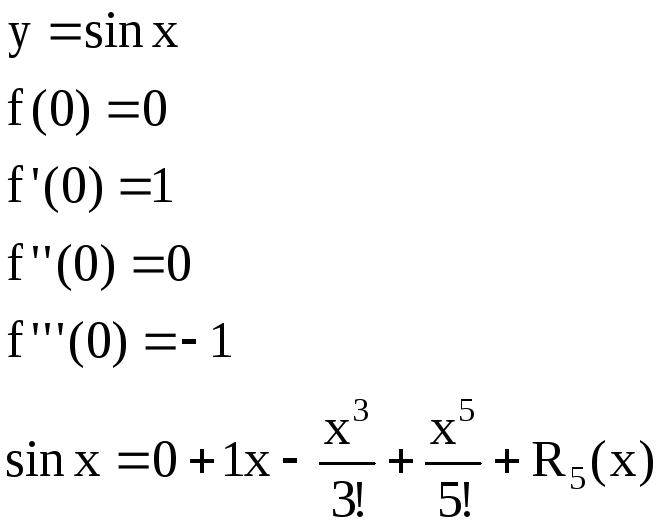
4)
![]()
5)
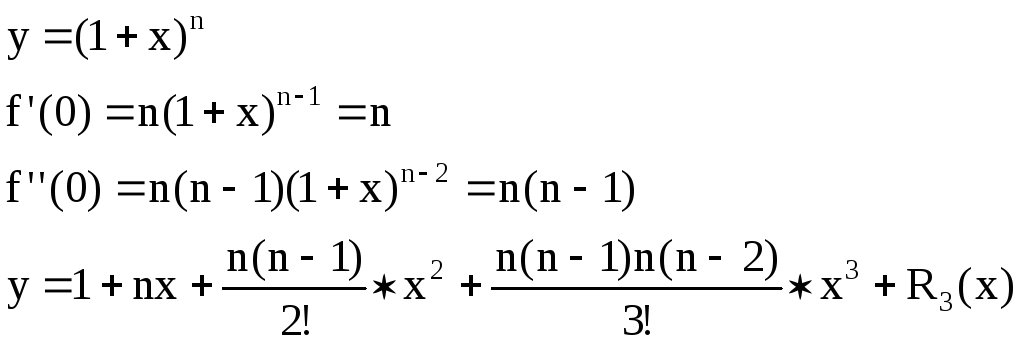
Треугольник Паскаля.
Исследование функции.
План общего исследования функции.
-
Область определения, четность, периодичность.
-
С помощью пределов выясняем непрерывность, ищем асимптоты.
-
С помощью первой производной – монотонность и экстремумы.
-
С помощью второй производной – выпуклость и вогнутость, точки перегиба.
-
График функции.
