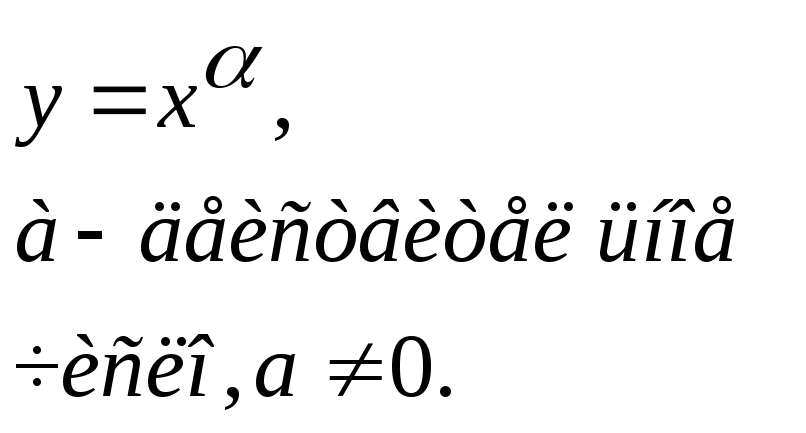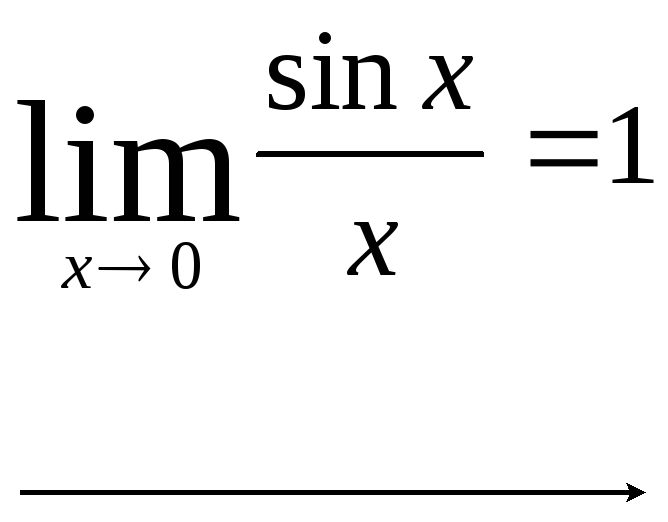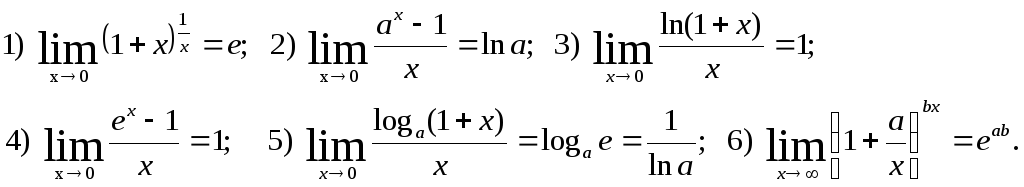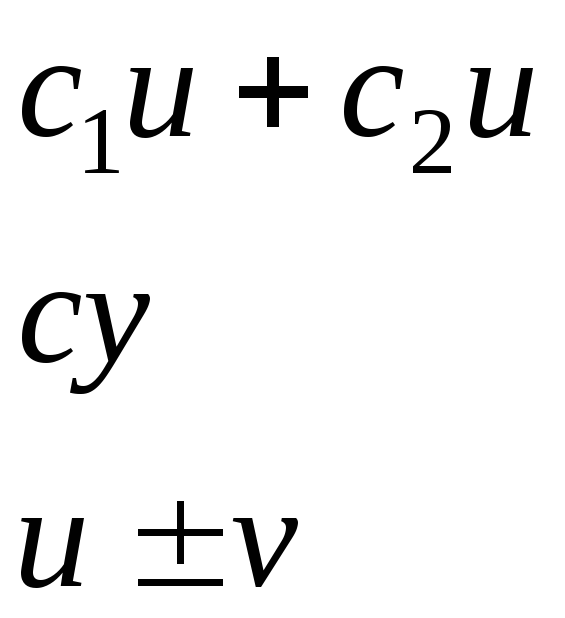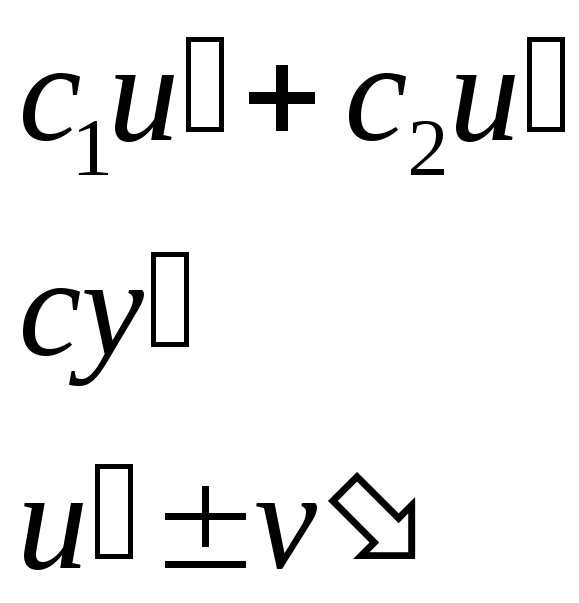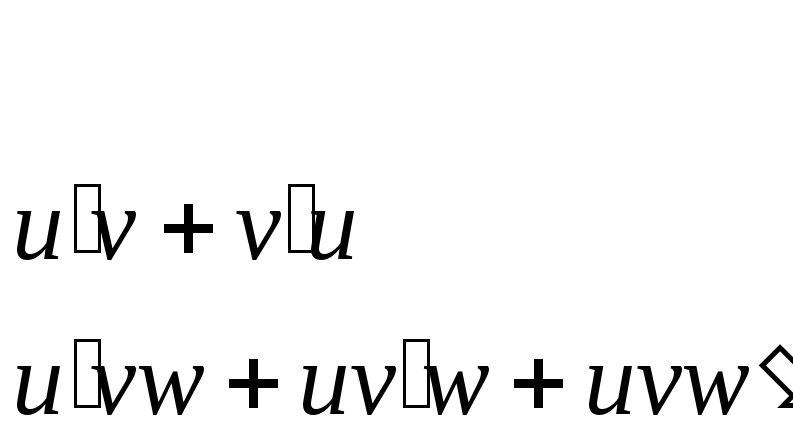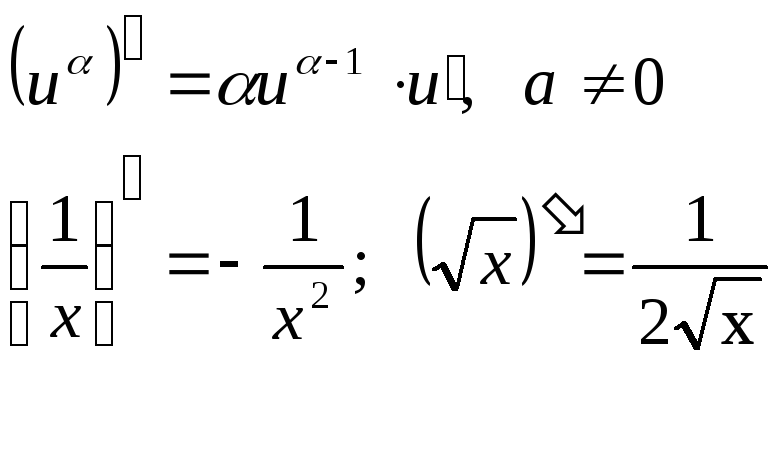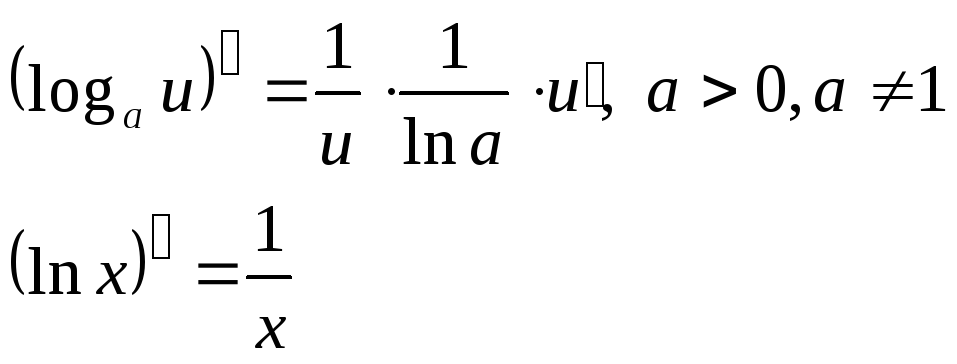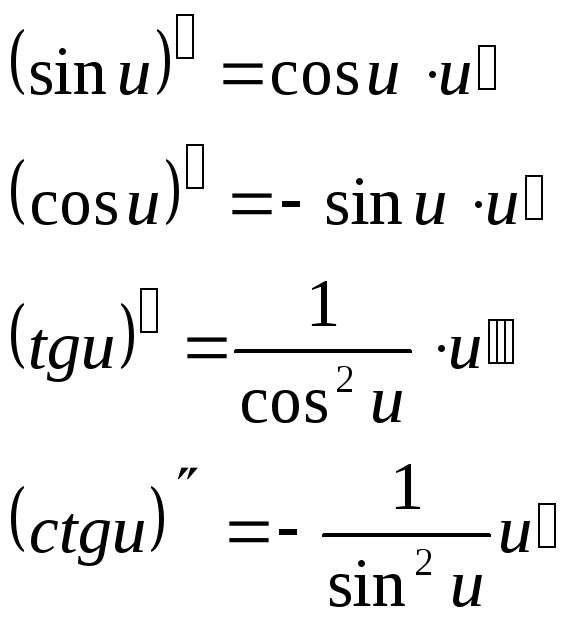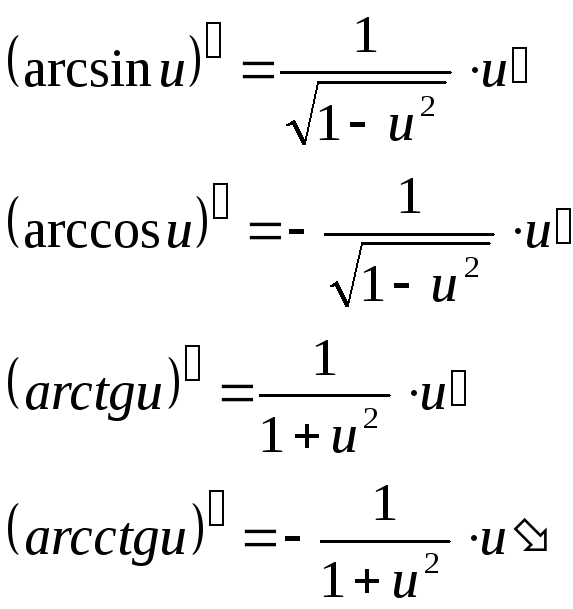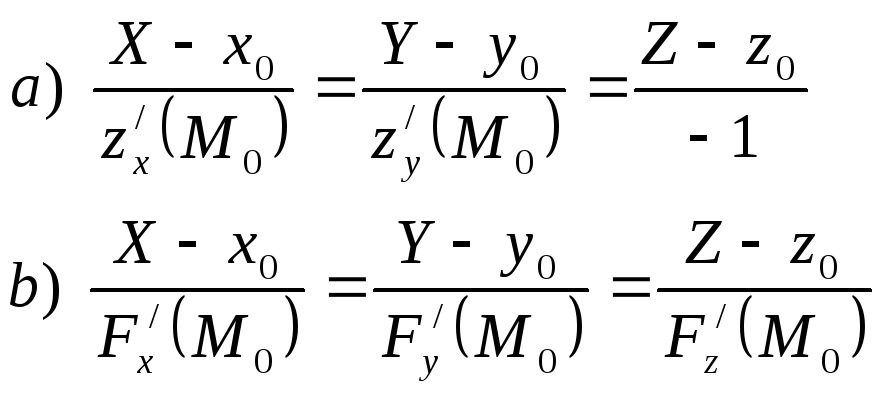- •Основные элементарные функции
- •Замечательные пределы
- •Уравнение касательной и нормали к графику функции
- •Основные правила дифференцирования
- •Производные основных функций
- •Гиперболические функции
- •Уравнение касательной плоскости и нормали к поверхности
- •Первообразная. Неопределенный интеграл.
- •1. Интегрирование подведением под знак дифференциала.
- •3. Интегрирование по частям.
- •Подставляя в формулу, получаем
- •Операции над комплексными числами
Линейное пространство. Определение и свойства
Определение линейного пространства
Пусть M —множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
паре элементов множества
 отвечает
элемент
отвечает
элемент 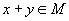 ,
называемый суммой x и y;
,
называемый суммой x и y;паре
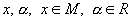 ,
, 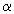 —
любое действительное число, отвечает
элемент
—
любое действительное число, отвечает
элемент 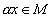 ,
называемый произведением числа
,
называемый произведением числа 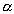 и
элемента x.
и
элемента x.
Будем
называть множество M линейным
пространством, если
для всех его элементов определены
операции сложения и умножения на
действительное число и для любых
элементов ![]() и
произвольных чисел
и
произвольных чисел ![]() справедливо:
справедливо:
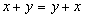 ,
сложение коммутативно;
,
сложение коммутативно;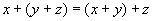 ,сложение
ассоциативно;
,сложение
ассоциативно;существует единственный нулевой элемент
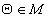 такой,
что
такой,
что 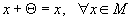 ;
;для каждого элемента существует единственный противоположный элемент -x такой, что
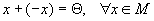 ,
, ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;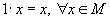 ;
;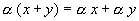 ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов;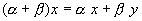 ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Равенства 1—8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы — векторами.
Примеры линейных пространств
Пример 1. Рассмотрим множество M арифметических векторов из Rn, компоненты которых — целые числа.
Это множество не является линейным пространством.
Действительно,
рассмотрим вектор
![]() )
и действительное число a=0.5.
Компоненты вектора
)
и действительное число a=0.5.
Компоненты вектора ![]() —
целые числа, он принадлежит множеству M,
но компоненты произведения
—
целые числа, он принадлежит множеству M,
но компоненты произведения ![]() не являются целыми числами, и, следовательно,
не являются целыми числами, и, следовательно,![]() не
принадлежит множеству M.
не
принадлежит множеству M.
Пример
2.Линейное пространство образуетмножество всех векторов,
принадлежащих пространствам ![]()
Пример
3.Линейным пространством
не является множество всех векторов
пространства ![]() ,
образующих острый угол с положительным
направлением оси ординат, так как при
умножении вектора из этого пространства
на отрицательное число получается
вектор, образующий тупой угол с
положительным направлением оси
ординат.Следовательно, он не принадлежит
исходному множеству векторов.
,
образующих острый угол с положительным
направлением оси ординат, так как при
умножении вектора из этого пространства
на отрицательное число получается
вектор, образующий тупой угол с
положительным направлением оси
ординат.Следовательно, он не принадлежит
исходному множеству векторов.
Пример 4. Линейным пространством не является множество натуральных чисел, так как при умножении натурального числа из этого множества на отрицательное число, получается отрицательное целое число, не принадлежащее множеству натуральных чисел.
Пример 5.Также линейным пространством не является множества всех отрицательных вещественных чисел, множества всех положительных вещественных чисел
Пример 6. Какое из
следующих предложений является аксиомой
линейного пространства
![]()
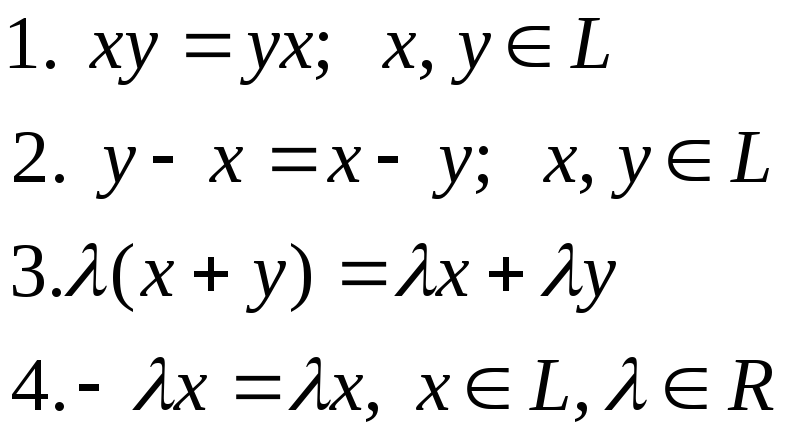
Ответ. 3.![]() .
.
Некоторые свойства линейных пространств
Утверждение 1. В произвольном линейном пространстве нулевой элемент — единственный.
Утверждение 2. В произвольном линейном пространстве нулевой элемент равен произведению произвольного элемента на действительное число 0.
Утверждение 3. В произвольном линейном пространстве каждому элементу отвечает единственный противоположный элемент.
Утверждение 4. В произвольном линейном пространстве противоположный элемент произвольного элемента x равен произведению x на действительное число -1.
Утверждение 5. В произвольном линейном пространстве для любых двух произвольных элементов x и y существует и единственна разность: x-y = x+(-1) ·y.
Квадратичные формы
Квадратичной
формой от
![]() переменных
переменных![]() называется сумма
называется сумма
![]() ,
где
,
где
![]() -
элементы квадратной матрицы
-
элементы квадратной матрицы
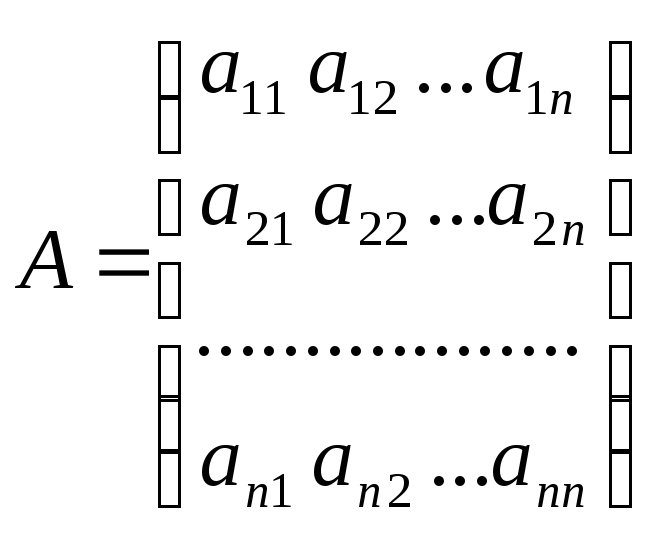 ,
называемой матрицей квадратичной формы.
,
называемой матрицей квадратичной формы.
![]() Квадратичная
форма называется симметрической, если
Квадратичная
форма называется симметрической, если
![]() .
В этом случае
.
В этом случае![]()
![]() .
Например, при
.
Например, при![]() ,
имеем
,
имеем
![]() ,
где
,
где
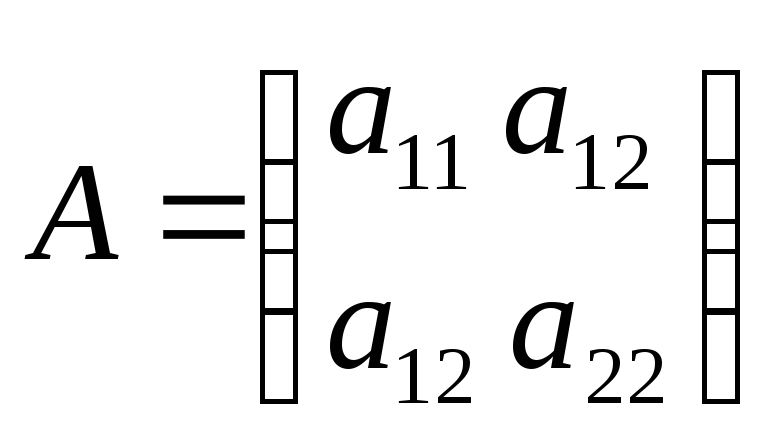 .
.
Симметрическая квадратичная форма называется положительно определенной, если выполнены неравенства

Симметрическая квадратичная форма называется отрицательно определенной, если выполнены неравенства

Пример.
Записать матрицу квадратичной формы
![]() .
.
Решение.
![]()
Пример.
Записать канонический вид квадратичной
формы
![]()
Решение.
Преобразуем
![]() .
Обозначим
.
Обозначим![]() .
Тогда канонический вид квадратичной
формы запишется так
.
Тогда канонический вид квадратичной
формы запишется так
![]() .
.
Пример.
Записать матрицу квадратичной формы
![]() .
.
Решение.
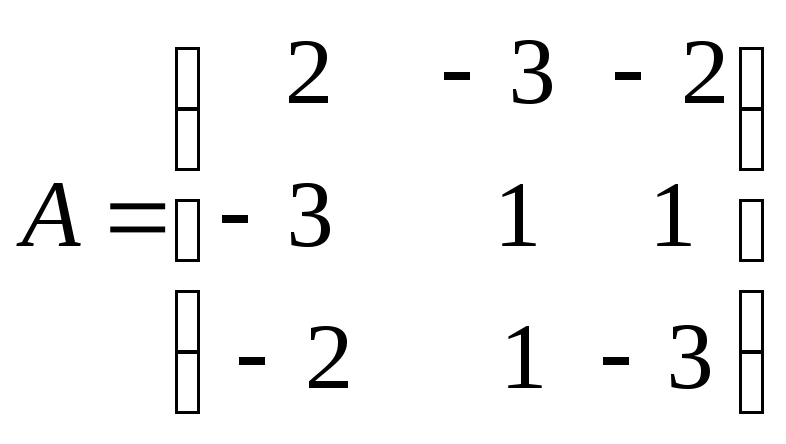
Пример. Положительно определенная квадратичная форма может иметь вид
1.
![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]()
Решение. Выписываем матрицы квадратичных форм и соответствующие определители
1.
![]() ,
,![]() положительно
определена.
положительно
определена.
2.
 не
явл.пол.опред.
не
явл.пол.опред.
3.
 не явл.пол.опред
не явл.пол.опред
4.
 не явл.пол.опред
не явл.пол.опред
Ответ.
![]()
СВОДКИ ФОРМУЛ
Основные элементарные функции
|
Наименование |
Формула |
Частные случаи |
|
1.Постоянная |
|
|
|
2.Степенная функция |
|
|
|
3. Показательная функция |
|
|
|
4.Логарифмическая функция |
|
|
|
5. Тригонометрические функции
|
| |
|
6. Обратные тригонометрические функции |
| |
Замечательные пределы
|
Первый замечательный предел:
Следствие:
|
|
Второй замечательный предел:
Следствие:
|
Уравнение касательной и нормали к графику функции
|
Наименование |
Уравнение |
|
1.
Уравнение касательной к графику
функции в точке
|
|
|
2.
Уравнение нормали к графику функции
в точке
|
|
Основные правила дифференцирования
|
Наименование |
Формула | |
|
Функции |
Производная | |
|
1. Линейная комбинация двух функций Частные случаи а) умножение на постоянный множитель; б) сумма (разность) двух функций. |
|
|
|
2. Произведение а) двух функций б) трех функций |
|
|
|
3. Частное двух функций |
|
|
|
4. Сложная функция |
|
|
|
5. Обратная функция |
|
|
|
6. Параметрическое задание функции |
|
|
|
7. Логарифмическое дифференцирование |
|
|
|
8. Показательно-степенная функция |
|
|
Обозначение:
![]()
Производные основных функций
|
Наименование |
Функция и производная |
|
1. Постоянная |
|
|
2. Степенная функция частный случай |
|
|
3. Показательная функция частный случай |
|
|
4. Логарифмическая функция частный случай |
|
|
5. Тригонометрические функции |
|
|
6. Обратные тригонометрические функции |
|
Примечание: При
![]() приведенные функции являются основными
элементарными функциями.
приведенные функции являются основными
элементарными функциями.
Гиперболические функции
|
Наименование |
Формула |
Производная |
|
1. Гиперболический синус |
|
|
|
2. Гиперболический косинус |
|
|
|
3. Гиперболический тангенс |
|
|
|
4. Гиперболический котангенс |
|
|
Уравнение касательной плоскости и нормали к поверхности
Уравнение поверхности задано:
а)
![]() - в явном виде; б)
- в явном виде; б)![]() - в неявном виде.
- в неявном виде.
|
Наименование |
Уравнение |
|
Уравнение
касательной плоскости в точке
|
|
|
Уравнение
нормали в точке
|
|
![]() -
координаты текущей точки касательной
плоскости или нормали.
-
координаты текущей точки касательной
плоскости или нормали.
Предел функции
Изучаемый материал:понятие предела функции и его вычисление; использование первого и второго замечательных пределов.
Пример1: Найти![]() .
.
Решение:![]() .
.
Пример2: Найти![]() .
.
Решение: 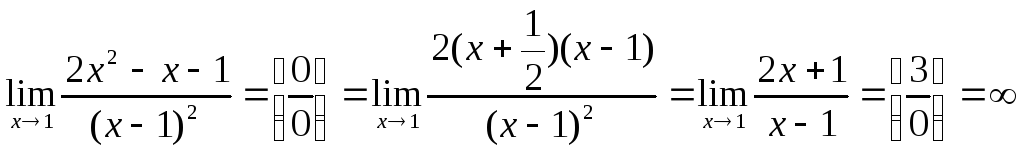 .
.
Пример3: Найти![]() .
.
Решение:Используем первый замечательный предел![]() .
.
Пример4:Найти![]() .
.
Решение:Используем второй замечательный предел![]() .
.
Справка:![]() ;
;![]() .
.
Непрерывность функции. Точки разрыва
Изучаемый материал:непрерывность функции в точке и в интервале; точки разрыва и их виды.
Пример: Проверить
является ли функция![]() непрерывной в точке
непрерывной в точке![]() .
В случае нарушения непрерывности
установить характер точки разрыва.
.
В случае нарушения непрерывности
установить характер точки разрыва.
Решение:![]() .
Функцияунеопределена в точке
.
Функцияунеопределена в точке![]() .
Значит
.
Значит![]() -
точка разрыва. Определим ее характер:
-
точка разрыва. Определим ее характер:![]() .
Получили
.
Получили![]() - точка разрыва второго рода.
- точка разрыва второго рода.
Правила дифференцирования основных элементарных функций
Изучаемый материал: основные правила дифференцирования и техника дифференцирования степенных, тригонометрических, обратных тригонометрических и логарифмических функций.
Пример 1:Найти
производную функцииу=5х3-2х+![]()
Решение:Данная функция есть алгебраическая сумма функций.
![]()
Пример 2:Найти
производную функции
![]()
Решение:![]()
Пример 3:Найти производную функцииу=sin3jи вычислить ее значение приj=p/3.
Решение:Это сложная функция с промежуточным аргументом sinj.
f¢ (j) = 3 sin2j (sin j)¢=3 sin2 j cos j.
Вычислим значение производной при j=p/3:
![]()
Пример 4:Найти
производную функции![]()
Решение: Это сложная функция с промежуточным аргументом cosх.
![]()
![]()
![]()
Пример 5:Найти
производную функции![]()
Решение: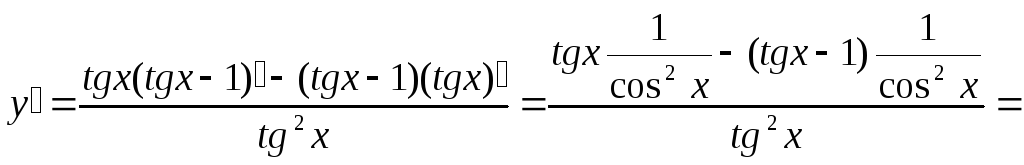
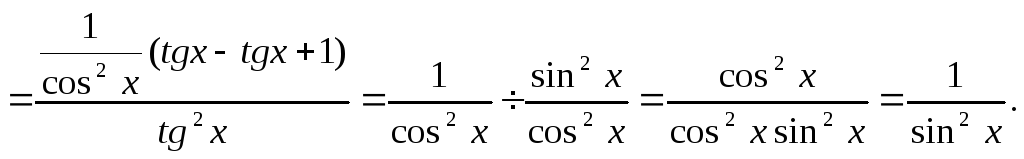
Пример
6:Найти производную функции![]() и вычислить ее значение приt=2.
и вычислить ее значение приt=2.
Решение:Сначала преобразуем функцию, используя свойства логарифмов:
![]()
Теперь дифференцируем по формулам:
![]()
Вычислим значение производной при t=2:
![]()
Частные производные. Градиент.
Определение.
Частной производной первого порядка
функции двух переменных
![]()
по
переменной х называется производная
по х при условии, что переменная у
является постоянной . Обозначается![]() . Точно также определяется частная
производная по переменной у. Обозначается
. Точно также определяется частная
производная по переменной у. Обозначается![]() .
При этом постоянной будет х.
.
При этом постоянной будет х.
Пример.
![]() . Найти частные производные первого
порядка.
. Найти частные производные первого
порядка.
Решение.
![]() .
.
Определение.
Частной производной
![]() второго
порядка функции двух переменных
второго
порядка функции двух переменных![]() называется производная по х частной
производной первого порядка
называется производная по х частной
производной первого порядка![]() при условии, что переменная у является
постоянной. Находится по формуле
при условии, что переменная у является
постоянной. Находится по формуле
![]()
Аналогично
определяется частная производная
![]() :
:
![]() .
Здесь х постоянна.
.
Здесь х постоянна.
Смешанная
частная производная второго порядка
![]() определяется по формуле:
определяется по формуле:
![]() или
или
![]()
Пример.
Найти смешанную частную производную
второго порядка
![]() ,
если
,
если
![]() .
.
Решение.
![]() ,
,
![]() .
.
Ответ.
![]() .
.
Определение.
Частной производной первого порядка
по одной из переменной
![]() функции
функции![]() называется
производная по этой переменной, при
условии, что две другие остаются
постоянными. Обозначаются
называется
производная по этой переменной, при
условии, что две другие остаются
постоянными. Обозначаются![]() .
.
Пример.
![]() .
Найти частные производные первого
порядка.
.
Найти частные производные первого
порядка.
Решение.
![]()
Определение.
Градиентом скалярного поля
![]() в точке
в точке![]() называется
вектор
называется
вектор![]() , определяемый по правилу
, определяемый по правилу![]() .
.