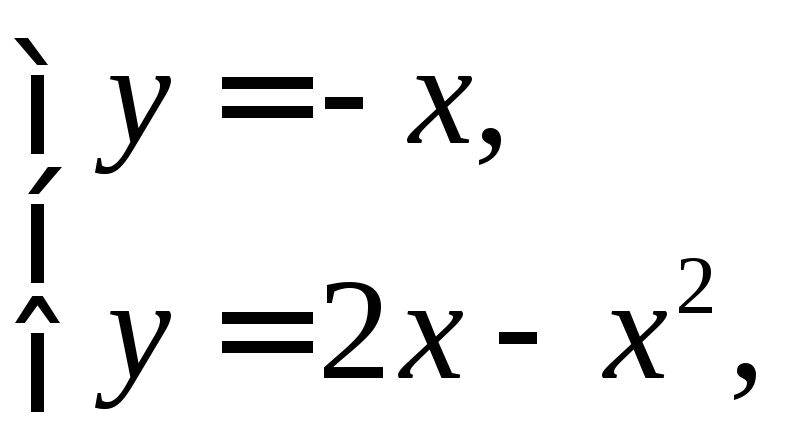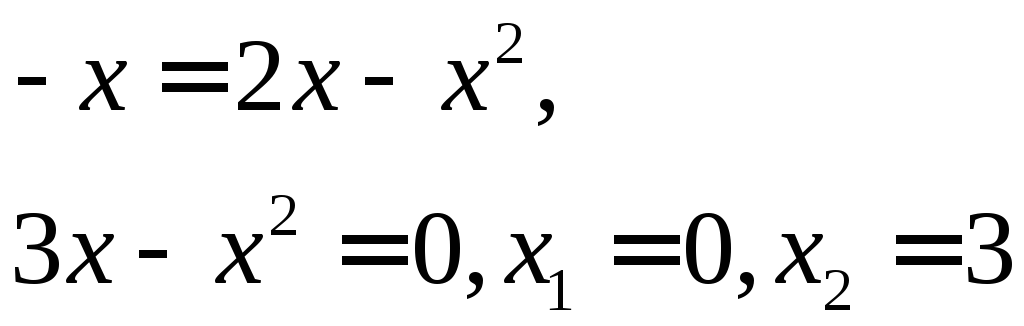- •Основные элементарные функции
- •Замечательные пределы
- •Уравнение касательной и нормали к графику функции
- •Основные правила дифференцирования
- •Производные основных функций
- •Гиперболические функции
- •Уравнение касательной плоскости и нормали к поверхности
- •Первообразная. Неопределенный интеграл.
- •1. Интегрирование подведением под знак дифференциала.
- •3. Интегрирование по частям.
- •Подставляя в формулу, получаем
- •Операции над комплексными числами
Первообразная. Неопределенный интеграл.
Определение. ФункцияF(х) называется первообразной для функцииf(х) на промежутке Х, если в любой точке х этого промежутка выполняется равенствоF′(х)= ƒ(х)
Примеры.
Функция F(х)=tg х является первообразной для функции
ƒ(х)=
![]() на интервале (-
на интервале (-![]() ,+
,+![]() ,)
х ≠
,)
х ≠![]() +π
n,
+π
n,
так как
![]()
2)
Функция F(х) =![]() является первообразной для функции
является первообразной для функции
![]() на интервале
(-1,1), так как
на интервале
(-1,1), так как
![]()
3)
Функция F(х)=lnx является
первообразной для функции ƒ(х)=![]() на интервале (0,+
на интервале (0,+![]() ),
так как (lnх)َ =
),
так как (lnх)َ =
![]()
Определение.
Совокупность всех первообразных для
функцииf(х) называется
неопределенным интегралом от функцииf(х) на Х и обозначается![]() .
.
Здесь
знак
![]() называется
знаком интеграла, выражениеf(x)dx– подынтегральным выражением, аf(x)
– подынтегральной функцией. ЕслиF(х)
– одна из первообразных дляf(х)
на Х, то
называется
знаком интеграла, выражениеf(x)dx– подынтегральным выражением, аf(x)
– подынтегральной функцией. ЕслиF(х)
– одна из первообразных дляf(х)
на Х, то![]() ,
где С- произвольная постоянная.
,
где С- произвольная постоянная.
Примеры.
1)
![]() ,
так как функцияF(х)=tgx– одна из первообразных для
,
так как функцияF(х)=tgx– одна из первообразных для![]() на Х .
на Х .
2)
![]() на интервале (
на интервале (![]() ),
так как функцияF(x)=lnxодна из первообразных
для ƒ
),
так как функцияF(x)=lnxодна из первообразных
для ƒ![]() на этом интервале.
на этом интервале.
Основные свойства неопределенного интеграла.
1.
![]() ,2.
,2.
![]() ,
,
3.
![]() ,
,
4.
![]()
Таблица интегралов.
1.
![]()
![]() ,
в частности,
,
в частности,
1.1
![]() ,
1.2
,
1.2![]() ;
2.
;
2.![]() , 3.
, 3.![]() ,
4.
,
4.![]() ,
,
5.
![]()
![]() ,
6.
,
6.![]() ,
,
7.
![]() , 8.
, 8.![]() ,
,
9.![]() , 10.
, 10.![]() ,
,
11
![]() ,
,
12.
![]() ,
,
13.
![]() ,
,
14.
![]() ,
,
15.
![]() ,
16.
,
16.![]() .
.
Примеры.
1)
![]() =
=![]()
Здесь
![]() .
.
Проверка.
![]() 2.
2)
2.
2)![]()
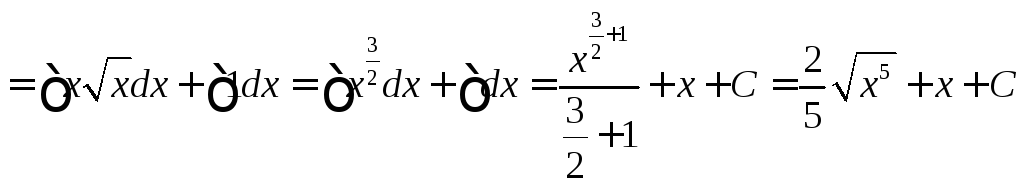 .
.
Проверка.
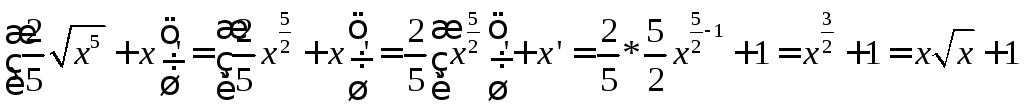 3)
3)![]() ,
используется табличный интеграл , здесь
,
используется табличный интеграл , здесь![]() ,
,
4)
![]() .
.
Проверка.
![]() .
.
5)
![]() ,
используется табличный интеграл, здесьa2 =10, тогдаa=
,
используется табличный интеграл, здесьa2 =10, тогдаa=![]() .
.
Основные методы интегрирования.
1. Интегрирование подведением под знак дифференциала.
Для использования метода запишем таблицу дифференциалов, которая легко получается из таблицы производных и таблицы интегралов. В первом случае применяем формулы для дифференциалов функции, записанных в обратном порядке, во втором – путем взятия знака дифференциала от обеих частей равенства. Таблица дифференциалов.
1.![]() 8.
8.![]()
2.![]() 9.
9.![]()
3.![]() 10.
10.![]()
4.![]() 11
11![]()
5.![]() 12.
12.![]()
![]()
6.![]() 13.
13.![]()
7.![]()
Примечание.
Формулы
для дифференциалов функции
![]() не меняются от того является лиxнезависимой переменной или есть некоторая
функцияu(t)
другой независимой переменнойt.
(свойства инвариантности формы первого
дифференциала )
не меняются от того является лиxнезависимой переменной или есть некоторая
функцияu(t)
другой независимой переменнойt.
(свойства инвариантности формы первого
дифференциала )
Поэтому
таблица дифференциалов будет иметь
место, если вместо xподставитьu(t).Cпомощью формулы для
дифференциала функции записанной в
обратном порядке![]()
некоторые
интегралы
![]() могут быть сведены к виду
могут быть сведены к виду
![]() ,
которые легко сводятся к табличным.
Здесь
,
которые легко сводятся к табличным.
Здесь
![]() .
.
Указанное преобразование называется «Подведение под знак дифференциала».
Примеры.
1)
![]() =
=![]() = =
= =![]() =
=
=![]() =
=![]()
2)![]() =
=![]() =
=![]()
![]() .
.
3)![]() =
=![]() =
=![]() =
=![]()
4)![]() =
=![]() =
=![]() =arcsin(
=arcsin(![]() )+C
)+C
5)![]()
![]() =
=
=![]() =
=![]()
2. Метод подстановки.
Иногда
удается подобрать в качестве новой
переменной такую дифференцируемую
функцию
![]() ,
что имеет место равенствоf(x)dx=q(
,
что имеет место равенствоf(x)dx=q(![]() (x))
(x))![]() (x)dx,
причем интеграл
(x)dx,
причем интеграл![]() легко вычисляется. Таким образом:
легко вычисляется. Таким образом:
![]() =
=![]()
Указанный
прием вычисления интеграла
![]() называетсяинтегрирование методом
замены переменной.
называетсяинтегрирование методом
замены переменной.
Примеры.
1)![]() (6x-5)dx.
Подстановка
(6x-5)dx.
Подстановка![]()
![]()
2)![]() ;
подстановкаt=ax+b,
;
подстановкаt=ax+b,
тогда
dt=d(ax+b)=(ax+b![]() dx=adx,
dx=
dx=adx,
dx=![]() ,
,
![]() =
=![]() =
=![]()
3)![]() .
.
Подстановка
![]()
![]() =
=![]()
4)![]() ;
подстановка
;
подстановка
![]()
![]()
5)![]() ;
подстановка
;
подстановка![]()
![]()
3. Интегрирование по частям.
Пусть
u(x) иv(x)-
дифференцируемые функции, Тогда
справедлива формула интегрирования по
частям:
![]() =uv-
=uv-![]() .
.
Указанная
формула позволяет свести вычисление
интеграла
![]() к вычислению интеграла
к вычислению интеграла
![]() .
Если принято решение об интегрировании
по частям то это целесообразно производить
следующим образом:
.
Если принято решение об интегрировании
по частям то это целесообразно производить
следующим образом:
1) подынтегральное выражение содержит в виде сомножителя функции lnx,arcsinx,arccosx,arctgx. В качествеu(x) выбирают указанные функции;
2)
подынтегральная функция имеет вид
P(x)![]() ,P(x)sinax,P(x)cosax, гдеP(x)-
многочлен относительно переменнойx.
,P(x)sinax,P(x)cosax, гдеP(x)-
многочлен относительно переменнойx.
В качестве u(x) выбираютP(x).
3)
подынтегральная функция имеет вид
![]() и т.д. После двукратного применения
формулы интегрирования по частям
получаем исходный интеграл с некоторым
коэффициентом. Решая уравнение находим
искомый интеграл.
и т.д. После двукратного применения
формулы интегрирования по частям
получаем исходный интеграл с некоторым
коэффициентом. Решая уравнение находим
искомый интеграл.
Примеры.
1)![]() ).
Полагаемu=lnx,dv=xadx,
тогдаdu=dlnx=(lnx)’dx=
).
Полагаемu=lnx,dv=xadx,
тогдаdu=dlnx=(lnx)’dx=![]() ,
,![]()
![]() 2)
2)
![]() Полагаемu=arcsinx,dv=xdx, тогда
Полагаемu=arcsinx,dv=xdx, тогда![]()
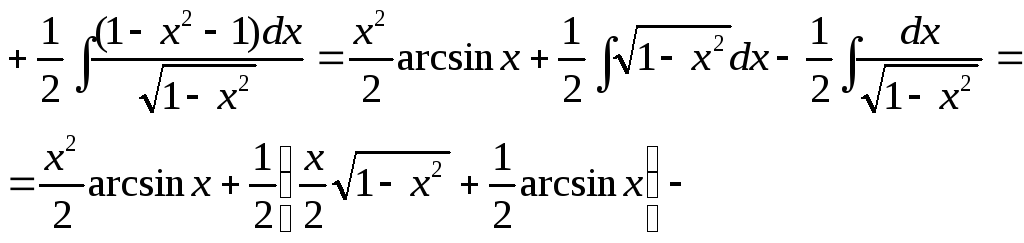
![]()
3)![]() Полагаем
Полагаем![]()
![]()
Для
вычисления![]() полагаем
полагаем![]()
Таким
образом
![]()
4)![]()
Полагаем
![]()
![]()
Чтобы
вычислить
![]() полагаем
полагаем
![]()
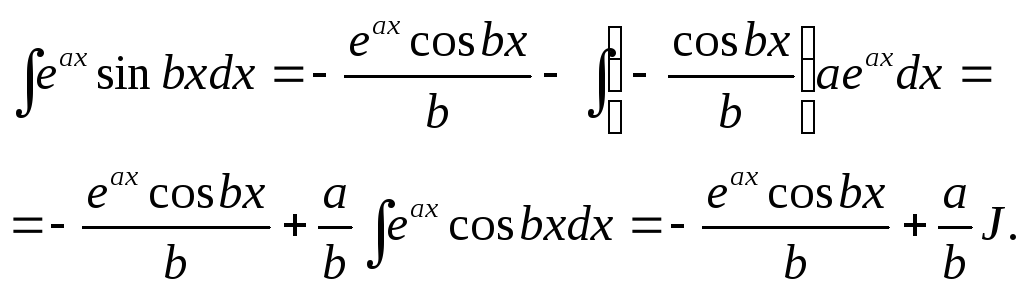
Далее
![]() или
или
![]() .
.
Определённый интеграл
Понятие определённого интеграла, свойства, основные правила и приемы интегрирования.
Пусть
![]() определена
на сегменте
определена
на сегменте![]()
Определение.Разбиение![]() сегмента
сегмента![]() задано, если заданы точки
задано, если заданы точки![]() такие, что
такие, что![]()
Обозначим
через
![]() длину
частичного сегмента
длину
частичного сегмента![]() Максимальную из этих длин обозначим
Максимальную из этих длин обозначим![]() которую назовём диаметром разбиения
которую назовём диаметром разбиения![]() В частичном сегменте выберем произвольную
точку
В частичном сегменте выберем произвольную
точку![]()
Определение.
Выражение![]() называется
интегральной суммой и обозначается
называется
интегральной суммой и обозначается![]()
Определение.
Число![]() называется пределом интегральных сумм
называется пределом интегральных сумм![]() при
стремлении диаметра разбиений
при
стремлении диаметра разбиений![]() к нулю, если для любого
к нулю, если для любого![]() существуют
такие
существуют
такие![]() что
из условия
что
из условия![]() при
любом выборе промежуточных точек
при
любом выборе промежуточных точек![]() следует неравенство
следует неравенство![]() .
При этом пишут
.
При этом пишут![]()
Определение.
Функция![]() называется интегрируемой на сегменте
называется интегрируемой на сегменте![]()
![]() если
для этой функции существует предел
если
для этой функции существует предел![]() её интегральных сумм
её интегральных сумм![]() при стремлении диаметра
при стремлении диаметра![]() разбиений
разбиений![]() к нулю.
к нулю.
Число
![]() называется определённым интегралом от
функции
называется определённым интегралом от
функции![]() в пределах от а до в и обозначается
в пределах от а до в и обозначается![]()
Числа
![]() и
и![]() – пределы интегрирования (
– пределы интегрирования (![]() – нижний предел,
– нижний предел,![]() – верхний предел).
– верхний предел).
Примечание. Переменную х под знаком определённого интеграла
можно
заменить на любую другую переменную:
![]() и т.д.
и т.д.
Теорема.
Если функция![]() непрерывна на сегменте
непрерывна на сегменте![]() ,
то она интегрируема на нём.
,
то она интегрируема на нём.
Пример.
1. Путь S, пройденный точкой за время![]() со скоростью
со скоростью![]() ,
естьS=
,
естьS=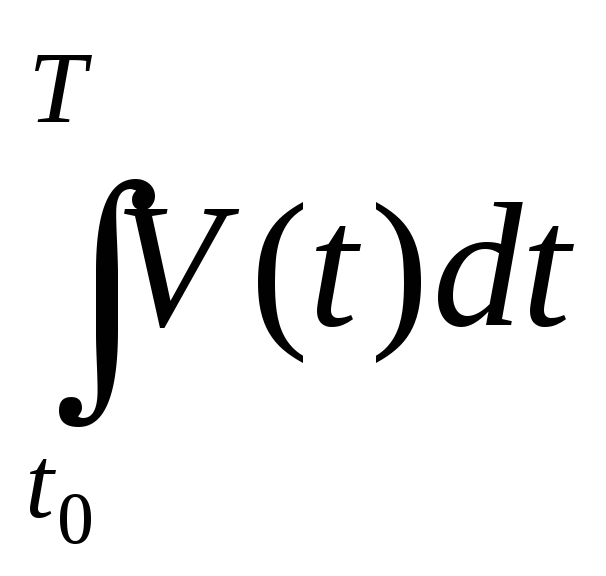 .
.
2.
Работа А, совершаемая над материальной
точкой переменной силой f(x),
есть![]() .
.
3.
Площадь криволинейной трапеции,
ограниченной сверху графиком
неотрицательной непрерывной функции
![]() ,
,
снизу
– осью Ох, с боков – прямыми
![]() равна
равна
![]()
Свойства определенного интеграла
Предполагаем,
что все рассматриваемые ниже функции
непрерывны на сегменте
![]() .
.
а)
Интеграл от суммы(разности) функций
![]() равен суме(разности) интегралов от этих
функций:
равен суме(разности) интегралов от этих
функций:![]() ;
;
б)
постоянная выносится за знак интеграла:
![]()
в)
определённый интеграл с равными нижним
и верхним пределами равен нулю:
![]() ;
;
г)
при перестановке пределов интегрирования,
знак определённого интеграла меняется
на противоположный:
![]()
г)
для любых a,b,cсправедливо![]()
д)
если
![]() на
на![]() , то
, то![]() ,
,
е)
если
![]() на
на![]() , то
, то![]() ,
,
ж)
![]() ,
,
г)
найдется такая точка
![]() , что
, что
![]() .
.
Следствие
. При
![]()
Пусть
![]() -
любая первообразная функции
-
любая первообразная функции![]() .
Тогда имеет место формула Ньютона-Лейбница
.
Тогда имеет место формула Ньютона-Лейбница![]() Замена переменной в определенном
интеграле: пусть функция
Замена переменной в определенном
интеграле: пусть функция![]() непрерывна
на
непрерывна
на![]() ,
а функция
,
а функция![]() непрерывна
вместе со своей производной на
непрерывна
вместе со своей производной на![]() ,
причем
,
причем![]() ,
тогда справедлива формула:
,
тогда справедлива формула:
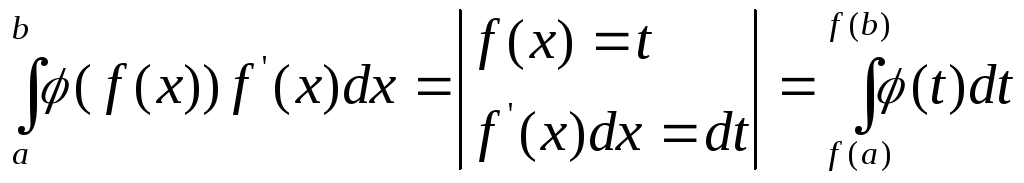 .
.
Пусть
![]() -
непрерывно дифференцируемые на
-
непрерывно дифференцируемые на![]() функции. Формула интегрирования по
частям имеет вид:
функции. Формула интегрирования по
частям имеет вид:![]()
Примеры.
1.
![]()
![]() ;
;
2.![]() ;
;
3.
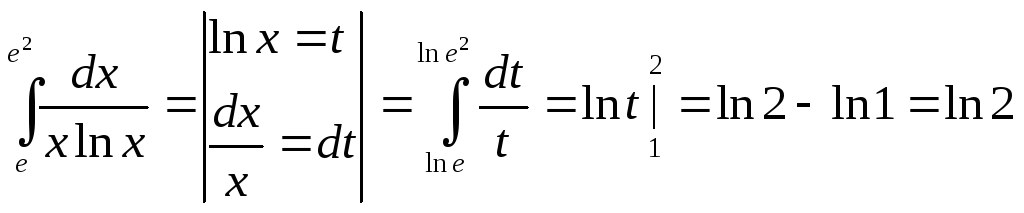 ;
;
4.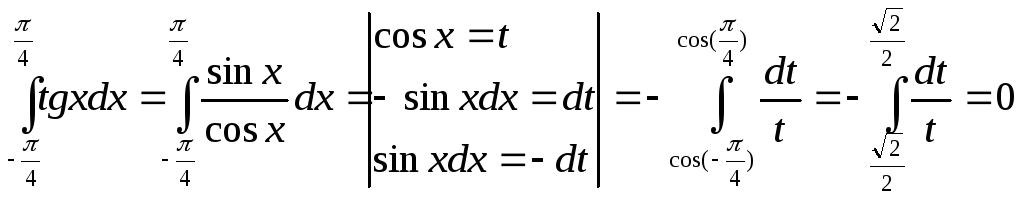 ;
;
5.
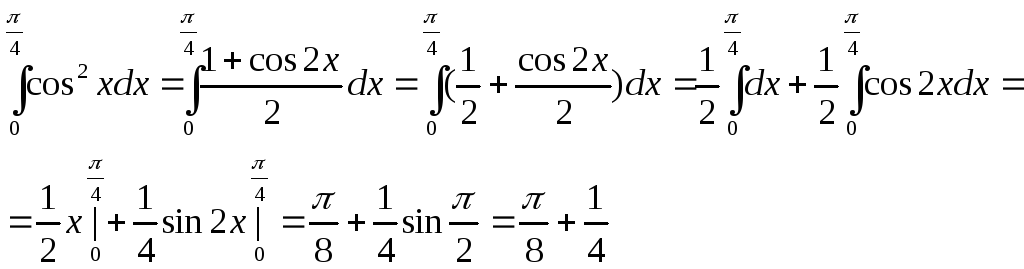
6.
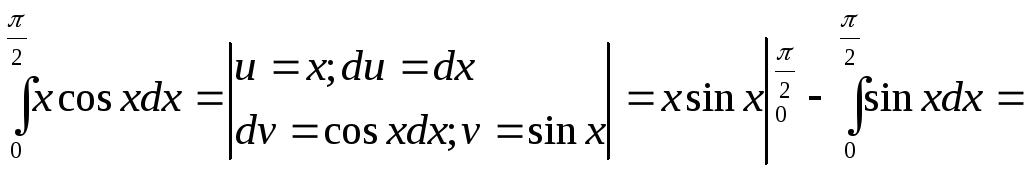
=![]() ;
;
7.
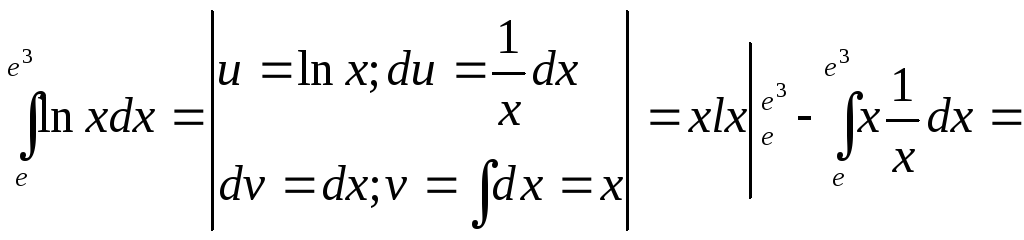
=![]()
![]() ;
;
8.
![]() ;
находим первообразную:
;
находим первообразную:
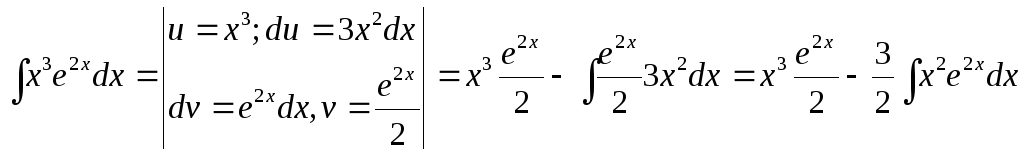 вычислим
вычислим
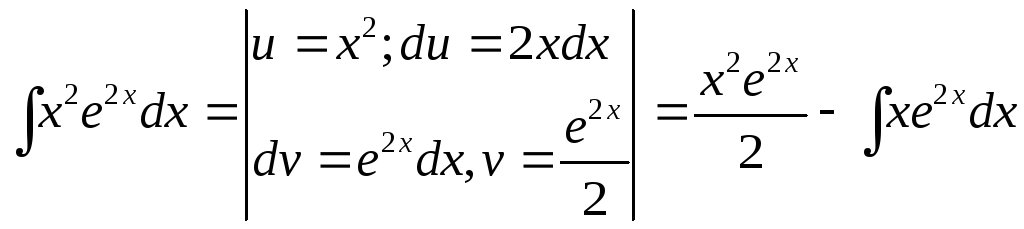 ,
,
вычислим
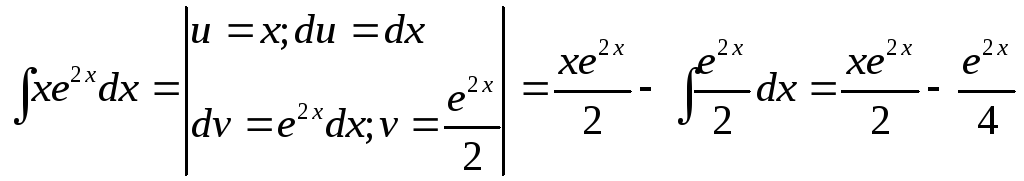
Подставим найденные первообразные и вычислим
![]() =
=![]()
=![]() .
.
Приложения определённого интеграла
Вычисление площади в прямоугольных координатах
Площадь криволинейной трапеции, ограниченной
кривой
y=f(x),![]() ,
прямымиx=aиx=bи осью
Ох находится по формуле
,
прямымиx=aиx=bи осью
Ох находится по формуле
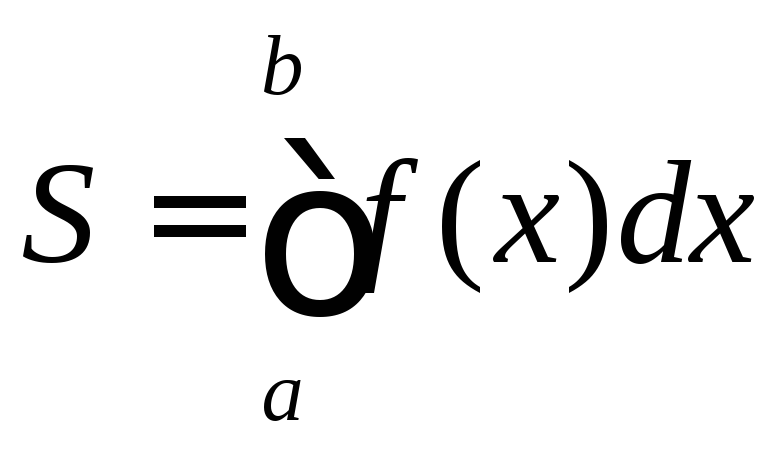 .
.
Пример.
Найти площадь фигуры, ограниченной
кривой![]() ,
прямой
,
прямой![]() и осью абсцисс.
и осью абсцисс.
Решение. Построим фигуру, ограниченную указанными линиями:


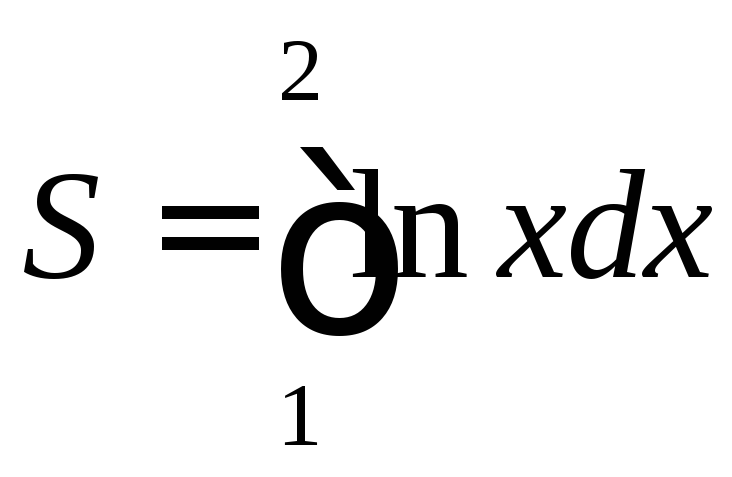 .
.
Применим
метод интегрирования по частям, полагая
![]() ,
тогда
,
тогда![]() .
.
Подставляем в формулу интегрирования по частям:
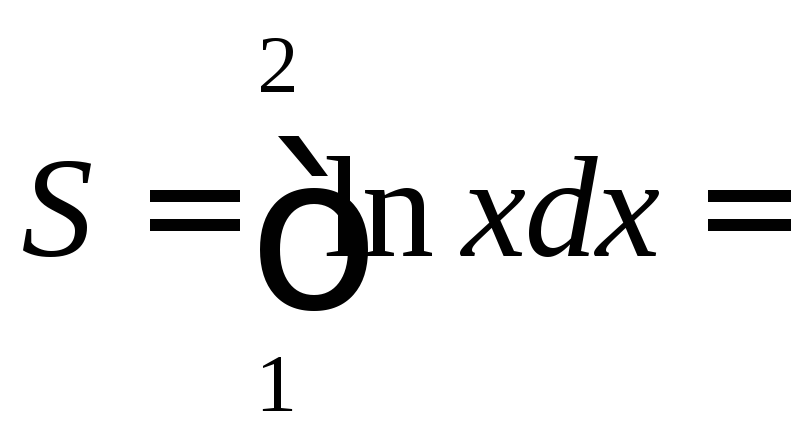
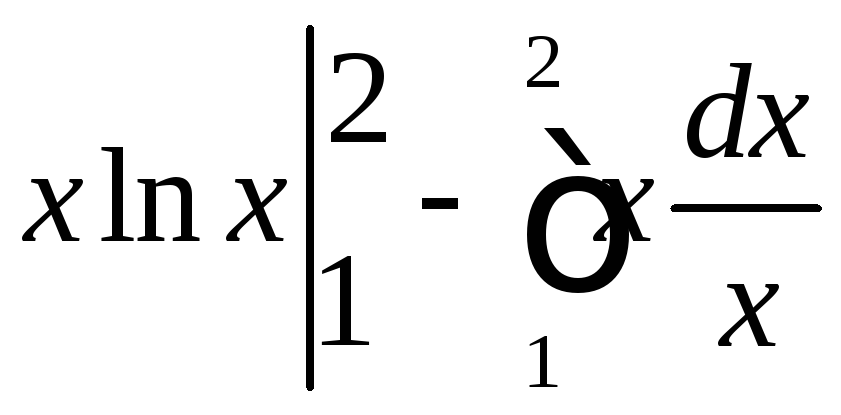 =
= =
=
=![]() .
.
Площадь
фигуры, ограниченной кривыми y=f(x),y=g(x)
и прямымиx=a,x=b, причем![]() ,
находится по формуле
,
находится по формуле
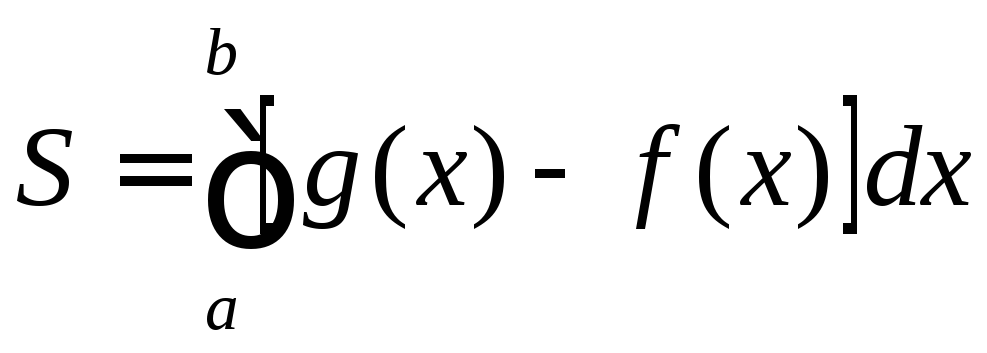 .
.
Площадь
фигуры, ограниченной кривыми
![]() ,
,![]() и прямыми у=с, у=d, причем
и прямыми у=с, у=d, причем![]() ,
находится по формуле
,
находится по формуле
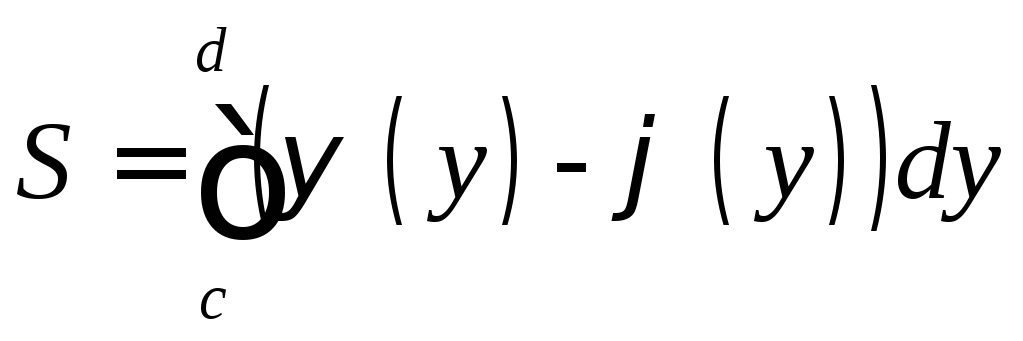 .
.
Пример.
Найти площадь фигуры, ограниченной
прямой![]() и
параболой
и
параболой![]() .
.
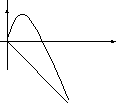
Решение. Находим точки пересечения прямой и параболы и строим ограниченную ими фигуру: