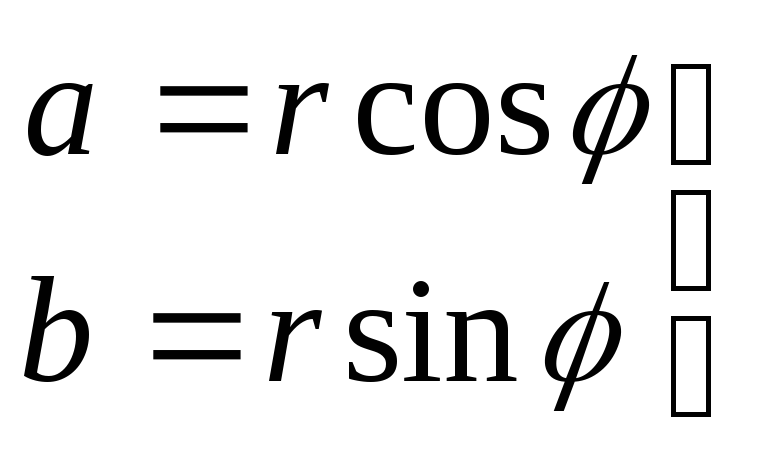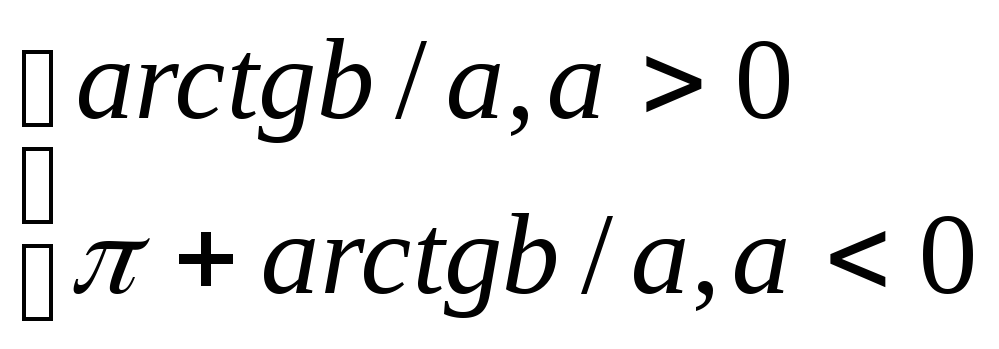Подставляя в формулу, получаем

=

=.

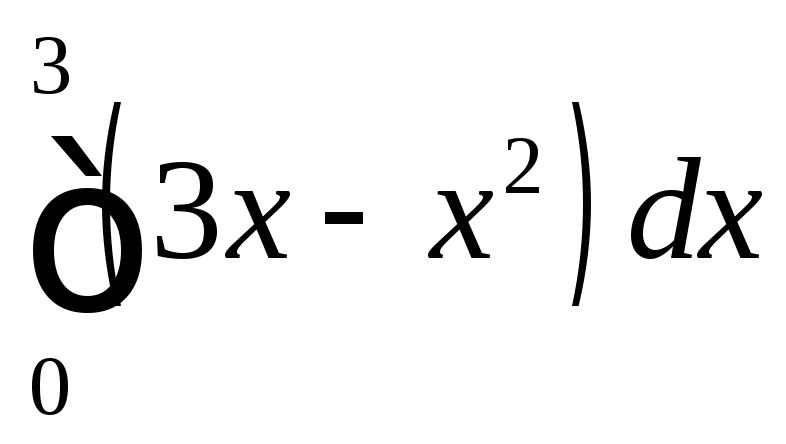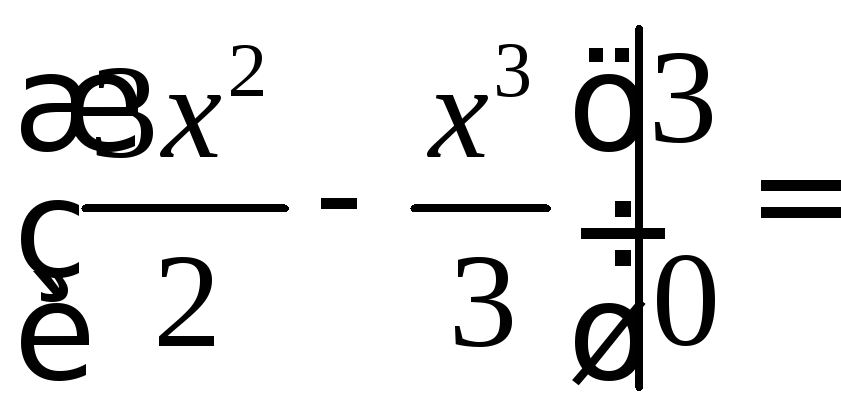
Пример.Вычислить площадь фигуры, ограниченной параболойи прямой.

Решение.

В этом случае удобно представить уравнения линий в виде

, .

Найдем точки пересечения

.

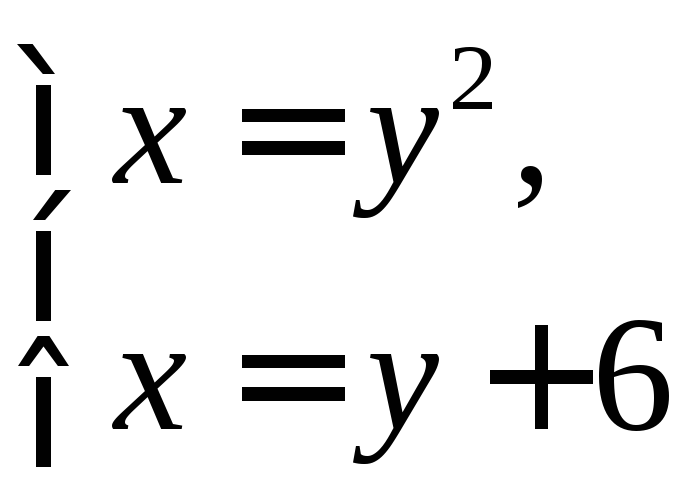
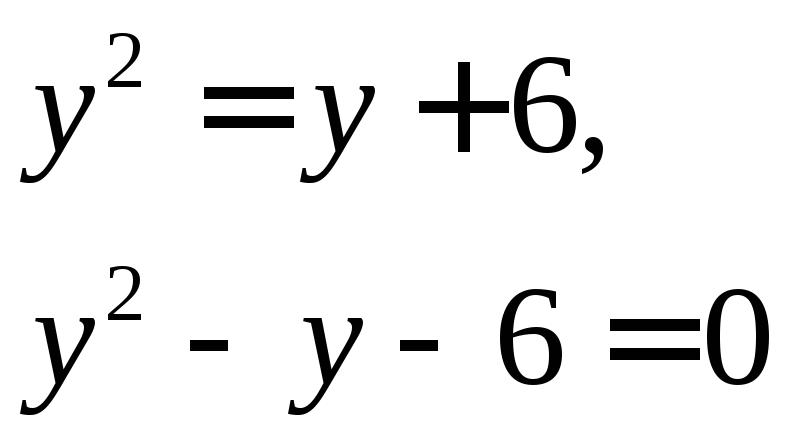Корни уравнения . Находим площадь фигуры

=.

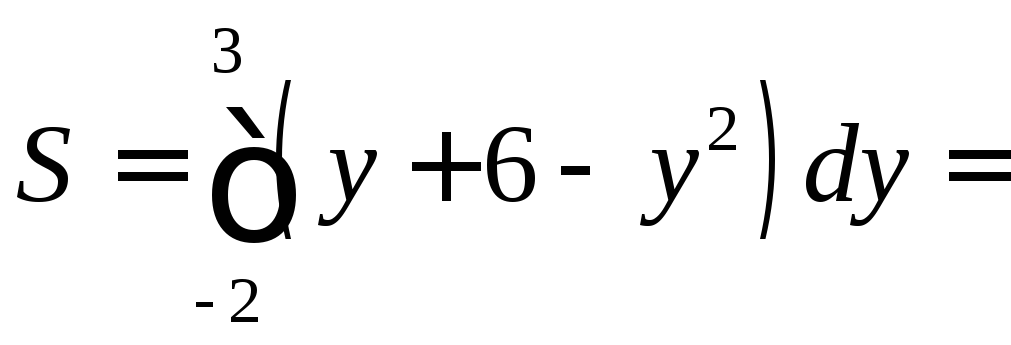
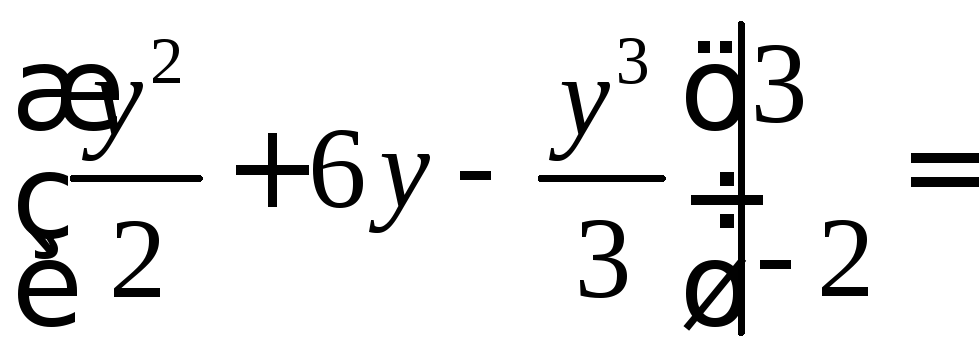
Числовые ряды

Определение. Бесконечная сумма вида , где (1)

- общий член ряда (произвольное число, как положительное так и отрицательное), называется числовым рядом.

Определение. Ряд (1) сходится , если сходится последовательность частичных сумм ряда

, то есть , где-конечное число, называемое суммой сходящегося ряда, а- частичная сумма ряда (1).

Утверждение. Из сходимости ряда (1) вытекает, что . Отсюда получаем, что

если , то ряд (1) расходится.

Рассмотрим ряд в виде геометрической прогрессии : , где- некоторое число. Приилиг.п. сходится и сумма ее равна, при, расходится.

Пример. Найти .

Решение. 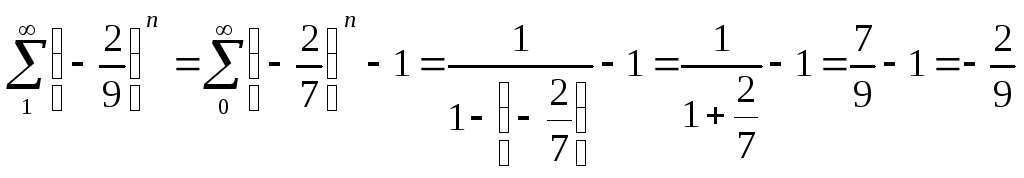. Здесь.

Пример. Найти сумму числового ряда .

Решение.

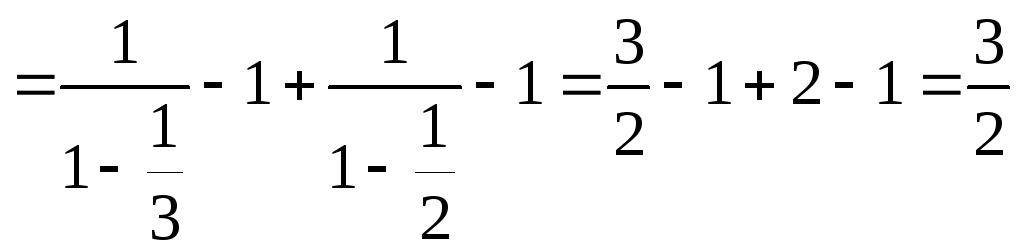
Знакоположительные числовые ряды

Определение. Числовой ряд называется знакоположительным, если все.

Рассмотрим знакоположительный ряд вида . (1)

Ряд сходится , еслии расходится, если.

Примеры сходящихся рядов: ,.

Примеры расходящихся рядов: .

Примечание: По отношению к ряду призаключение о его поведении

не изменяется, то есть, он сходится, если и расходится, если.

Рассмотрим ряд вида , (2)

где - многочлен степениmотносительно переменного натуральногоnс действительными коэффициентами,

- многочлен степени kотносительно переменного натуральногоncдействительными коэффициентами

При этом числа неотрицательные целые числа, не равные одновременно нулю.

Например - многочлен степени 3,- многочлен степени 4.

Утверждение. Если , (3)

то ряд (2) сходится, в противном случае, то есть когда , (4)

то ряд (2) расходится.

Пример. Ряд расходится, так каки выполнено условие (4).

Пример. Ряд сходится, так каки выполнено условие (3).

Пример. Ряд сходится, так каки выполнено условие (3).

Пример. расходится, так каки выполнено условие (4).

Пример. расходится, так каки выполнено условие (4).

Пример. Найти .

Решение.

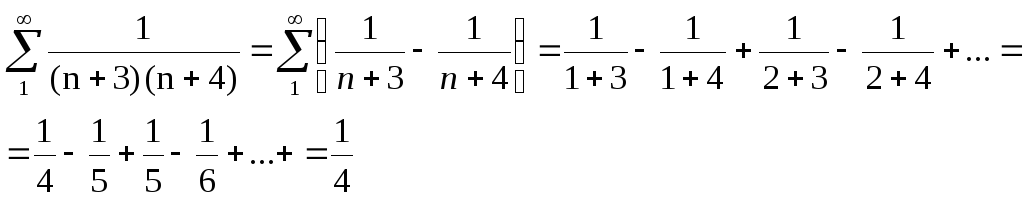
Признак сравнения. Пусть даны два знакоположитедьных ряда A)В).

Если , где, то ряды А и В сходятся или расходятся одновременно.

Пример. Указать сходящиеся числовые ряды.

1) 2)3)4)

Решение. Для сравнения возьмем ряд . Ясно, что в (1) надо взять, в (2) надо взять, в (3) надо взять, в (4) надо взять. Это делается из следующих соображений: В (1) отбрасывается слагаемое, в (2) отбрасывается -4, в (3) отбрасываетсяв (4) отбрасывается. После этого остаются ряды,

, ,или после преобразований,,,. Отсюда ряд (1) сходится так как,. Ряд (2) расходится так,как.

Ряд (3) расходится так,как . Ряд (4) сходится так,как.

С использованием признака сравнения заключение о характере сходимости ряда

проводится следующим образом: в многочленах иоставим старшие члены, то есть слагаемыеи. В результате получим ряд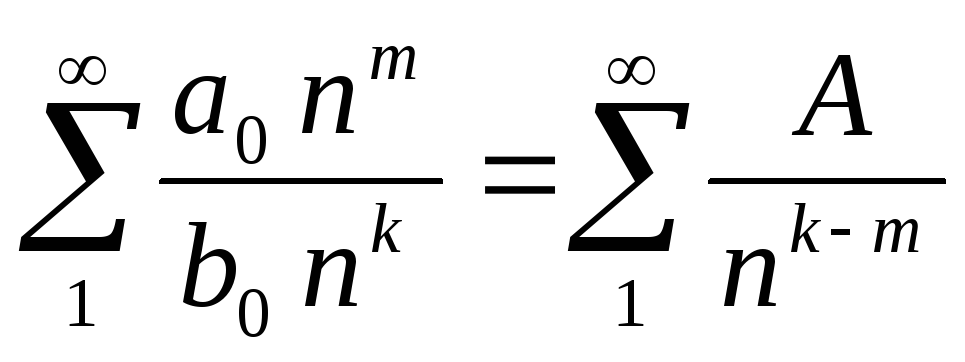, где- постоянная. Отсюда приили то же самое, ряд сходится

и при или, ряд расходится.

Знакочередующиеся ряды

Ряд вида , где(5) называется знакочередующимся рядом.

Признак Лейбница. Если члены ряда (5) по модулю монотонно убывают с ростом , то есть, начиная с некоторогоnи, то ряд (5) сходится . Если нарушено хотя бы одно из указанных условий, то ряд расходится.

Пример. Даны числовые ряды:

А)

В)

Выяснить характер сходимости этих рядов. Ответ. А сходится, В расходится.

Решение. Для ряда А модулем общего члена ряда является . Ясно, что он монотонно уменьшается , начиная сn=1,. Условия признака Лейбница выполнены, следовательно ряд А сходится.

Для ряда В модулем общего члена ряда является . Очевидно, что второе условие признака Лейбница не выполнено, так как, следовательно ряд В расходится.

Определение. Знакочередующийся ряд сходится абсолютно, если сходится ряд составленный из абсолютных значений его членов, то есть если сходится ряд .

Утверждение. Если знакочередующийся ряд сходится абсолютно, то он просто сходится, то есть справедлива схема:

-сходится - сходится

Определение. Если ряд сходится, а рядрасходится ( расходится абсолютно), то говорят, что рядсходится условно.

Пример. Укажите правильное утверждение относительно сходимости знакочередующихся рядов:

А) и В). Ответ. А расходится, В сходится условно.

Обоснование. , то есть нарушено второе условие признака Лейбница, следовательно ряд А расходится. Относительно ряда В). Так как коэффициентыубывают монотонно с ростоми, то есть выполнены оба условия признака Лейбница, ряд В) сходится. Но рядрасходится, следовательно ряд В) сходится условно.

Степенные ряды

Ряд вида называется

степенным рядом. Здесь - коэффициенты ряда (действительные числа),- центр ряда.

Существует положительное число такое , что степенной ряд сходится при всехиз интервалаи расходится при всех, лежащих вне этого интервала.

Такое называется радиусом сходимости степенного ряда, а интервал- интервалом или областью сходимости.

Радиус сходимости можно найти по формулам

или

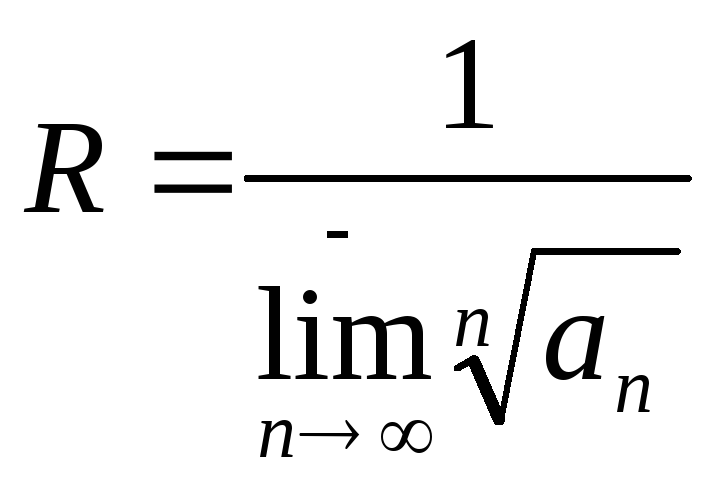
Пример. Найти область сходимости степенного ряда и исследовать сходимость на границе этой области.

Решение. Здесь . Радиус сходимости

. Центр ряда , интервал или область сходимости. На левом конце приполучим

числовой ряд который расходится, так как. На правом конце приполучим числовой ряд

, который расходится, так как . Таким образом областью сходимости степенного ряда является интервал.

Элементы операционного исчисления

Определение. Преобразованием Лапласа функции называется интеграли обозначается. Таким образом,

, где

- действительная переменная, - комплексная переменная. При этом функцияназывается оригиналом,-изображением.

Условия, которым должен удовлетворять оригинал :

1) при

2) Не иметь знаменатель, который обращается в ноль. Например, функция не может быть оригиналом.

3) С возрастанием модуль функциине может расти быстрее некоторой показательной функции, то есть,, где.

Например, функция не может быть оригиналом, так как при любых числах, данная функция растет быстрее чем функция, то есть нарушается условие (3).

Свойство линейности изображения

Обозначим .Пусть оригиналыиимеют изображенияи. Тогда. Таким образом, изображением суммыявляется.

Пример 1. Найти изображение функции .

Решение. Имеем . Таким образом, изображением функцииявляетсятак, как изображением 1 согласно таблице является, а изображениемявляется.

Пример 2. Найти изображение функции 3.

Решение. Имеем . Таким образом, изображением функцииявляется.

Пример 3. Какой оригинал соответствует изображению .

Решение. Согласно (4) таблицы изображений имеем при оригинал вида

Пример 4. Найти изображение решения задачи Коши:

Решение. Имеем , где

или . Отсюда находим:,

. Ответ:

Пример5. Записать в изображениях решение задачи Коши вида

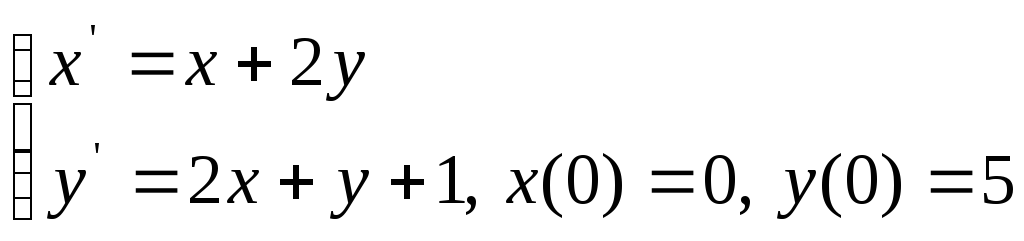
Решение. Имеем

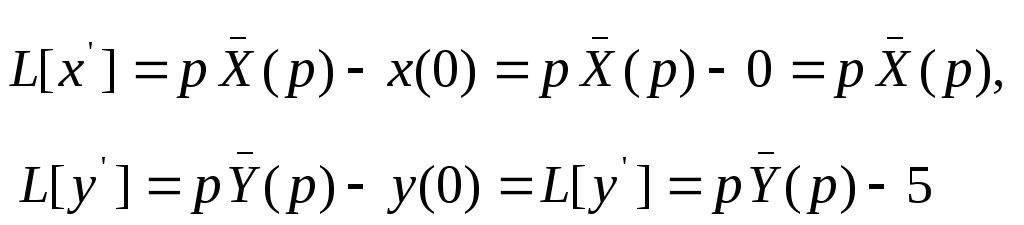
Далее ,. Отсюда

Ответ

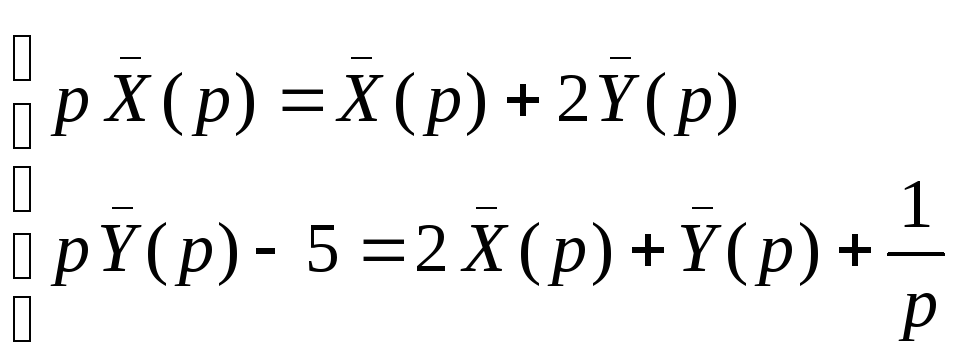
Таблица изображений

Nпп	Оригинал	Изображение
1	1
2
3
4
5
6
7
8
9
10
11
12
13
14
15	-производная	, где -изображение
16	-вторая производная	, где -изображение
17	- третья производная
18	- -я производная
19
20
21
22

Комплексный анализ.

Формы комплексного числа

Наименование формы	Формула	Геометрическое представление
1.Алгебраическая	z=a+ib
2.Тригонометрическая	z=r(cos+i sin)
3.Показательная	z=rei
Обозначение: i – мнимая единица, гдеi2=-1 z – комплексное число a,b– действительные числа a– действительная часть ib– мнимая часть r– модуль, - аргумент,	Соотношения: