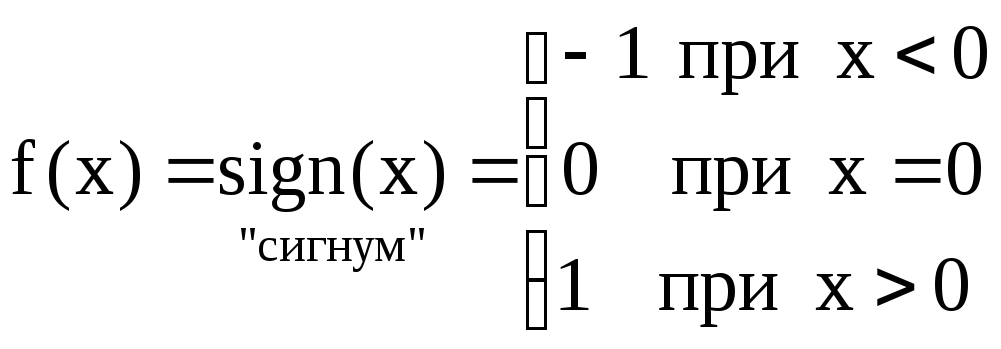Используем бином Ньютона для доказательства неравенства:
Отсюда заключаем,
что
,
а значит
.
Следствия из теоремы:
1)
2)
|
3) |
|
4)
Доказательство:
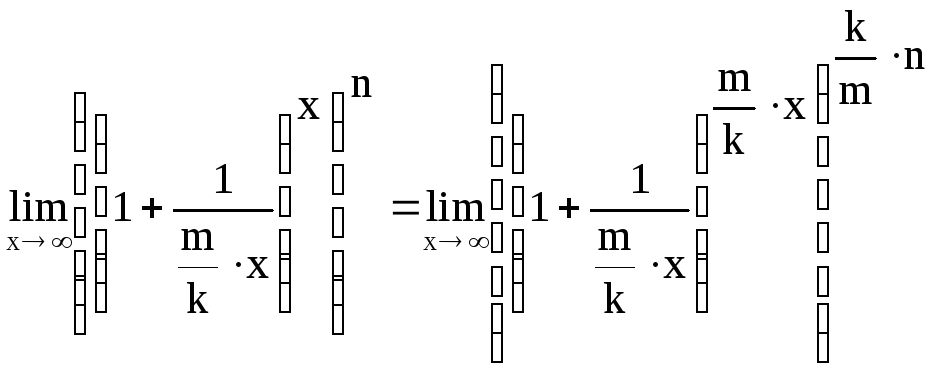
Если принять, что
,
то
Примеры:
1)
Учитывая, что
.
2)
.Отсюда
A = e.
Учитывая, что
.
Сравнение б.м.в.
Пусть
– бесконечно малые величины при
,
т.е.
.
Определение 1.
Если
,
то
– б.м.в. одного порядка малости.
Определение 2.
Если
,
то
– б.м.в. более высокого порядка, чем
.
–
более высокого
порядка, чем
("о" – читается как "о малое").
–
более низкого
порядка, чем
("О" – читается как "О большое").
Определение 3.
Если
,
то
и
эквивалентны –
.
Следствие из
определения 3:
при
.
Теорема. Если
и
эквивалентны (
)
, то
и
.
Доказательство:
Пусть
– бесконечно малые величины при
и они эквивалентны (
).
Тогда .
Непрерывность.
Определение
1. Пусть функция
определена в окрестности точки
,
тогда функция непрерывна в
,
если
.
Определение
2.
Функция
непрерывна, если
.
Определение
3. Функция
непрерывна в точке
,
если
.
Приращение
аргумента
.
Приращение
функции
.
Определение
4. Функция
непрерывна в точке
,
если
.
Если функция не
является непрерывной в точке
,
то эта точка – точка разрыва.
Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).
Определение 5.
Функция
непрерывна в точке
справа, если
.
Определение 5.
Функция
непрерывна в точке
слева, если
.
Функция непрерывна
на отрезке
,
если она непрерывна в каждой внутренней
точке этого отрезка и односторонне
непрерывна на его концах.
Теоремы о непрерывных функциях.
Теорема 1. Сложение, умножение, деление непрерывных функций – непрерывны.
Доказательство:
Пусть
и
.
Тогда
.
Доказательство для умножения и деления аналогично доказательству для сложения.
Теорема 2. Композиция непрерывных функций непрерывна:
Функция
непрерывна в точке
,
если g(x)
непрерывна
в точке
и f(y)
непрерывна в
.
Теорема 3. Все элементарные функции непрерывны.
Разрыв функции.
Разрыв первого рода.
Пусть
и
существуют:
I.
Если
,
то в точке
функция
испытывает разрыв скачок первого рода.
Примеры:
2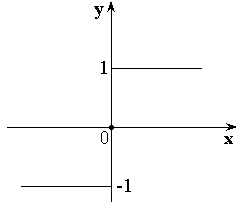
)
– целая часть числа x.
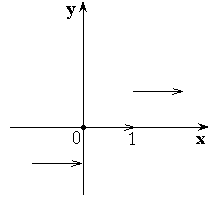
3)
– дробная часть от числа
x.
I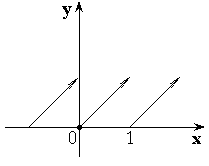
I.
Если
,
то в точке
функция
испытывает устранимый разрыв первого
рода.
Примеры:
1)
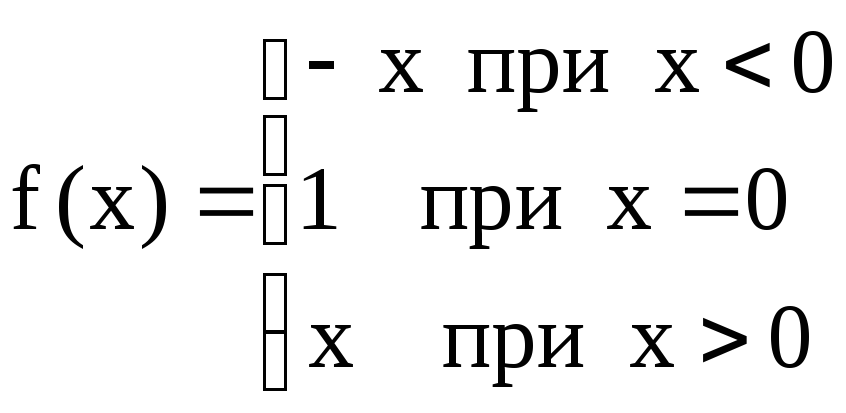
2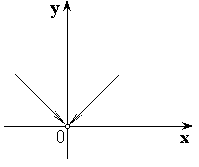
)
Рисунок.
3)
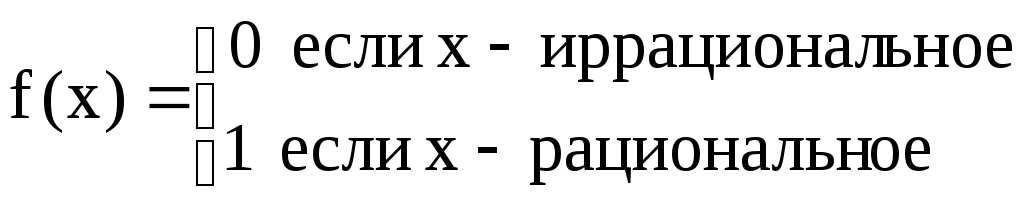
4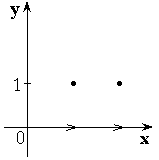
)
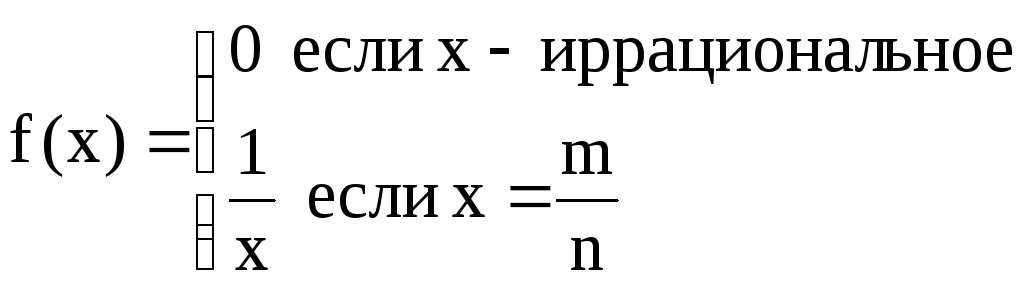
Рисунок.
Разрыв второго рода.
Функция испытывает
разрыв второго рода, если
– не
существует.
Свойства функции непрерывной на замкнутом отрезке.
Пусть функция
непрерывна на замкнутом отрезке
.
Т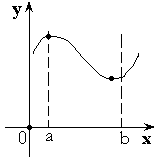
еорема
1. Функция
принимает наибольшее и наименьшее
значение на
.
Или
,
где
.
Теорема 2.
Функция принимает все свои промежуточные
значения на
.
Или
,
где
– область значений.
Т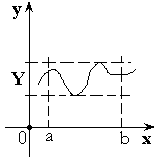
еорема
3. Если функция
принимает на концах отрезка
значения разных знаков, то внутри отрезка
найдется точка, в которой
.
Или
.
П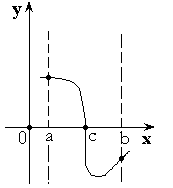
роизводная
функции.
Пусть функция определенна в окрестности точки .
Тогда
,
где
и
.
Производная
функции в точке есть предел отношения
приращения функции (
)
и приращения аргумента (
),
когда
.
Дифференцируемость.
Механический смысл производной.
Производная – это скорость изменения функции.
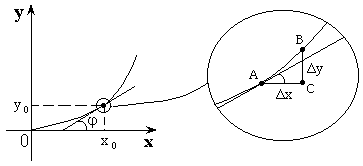
Геометрический смысл производной.
Производная –
это тангенс наклона угла касательной
к оси
.
Не мое!!!!
при
Рис.
Вычисление производной.
Если функция дифференцируема в точке, то она непрерывна в этой точек.
при
при
,
следует
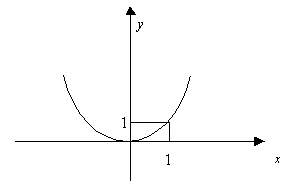
Обратное не верно.
Пример:
1)
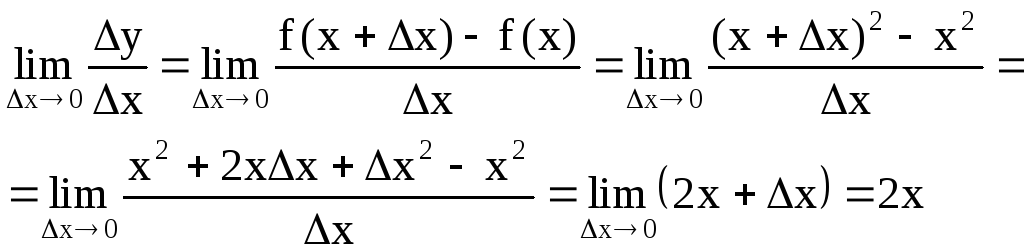
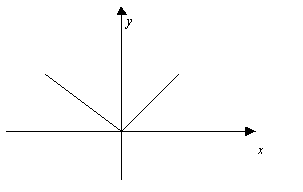
Таблица производных.
Правила дифференцирования.
1)
Производная
от суммы равна сумме производных:
.
Доказательство:
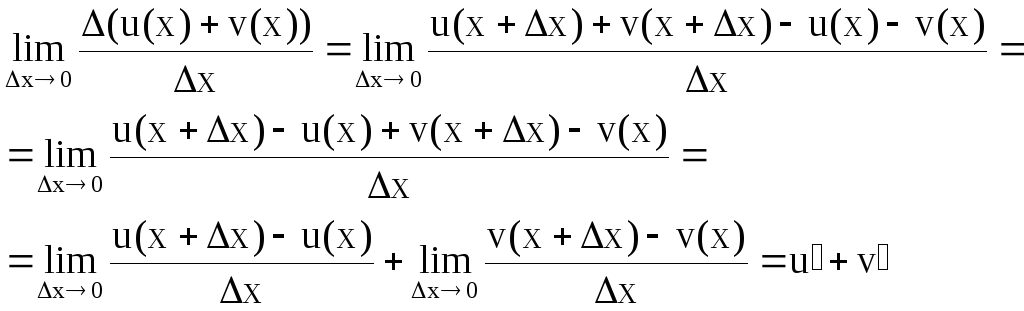
2)
Постоянный множитель выноситься за
знак производной:
.
3)
Производная произведения:
.
Доказательство:
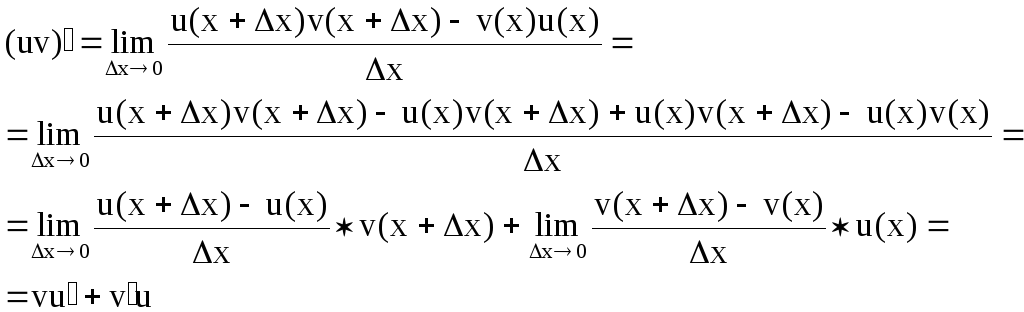
4)
Производная дроби:
.
Доказательство:
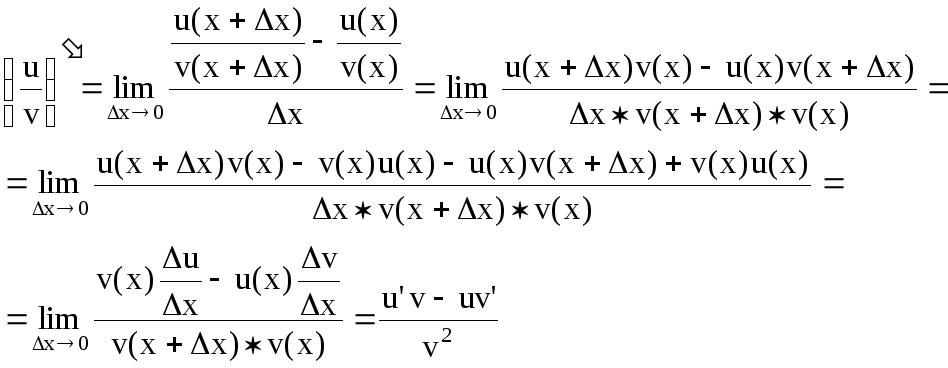
Вывод формул для производных.
1)
2)
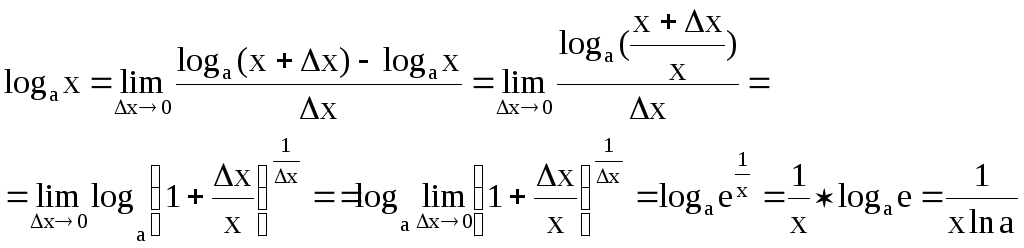3)
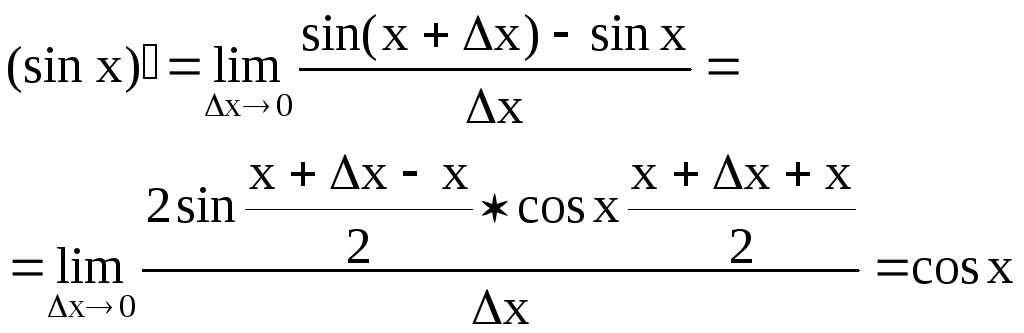
4)
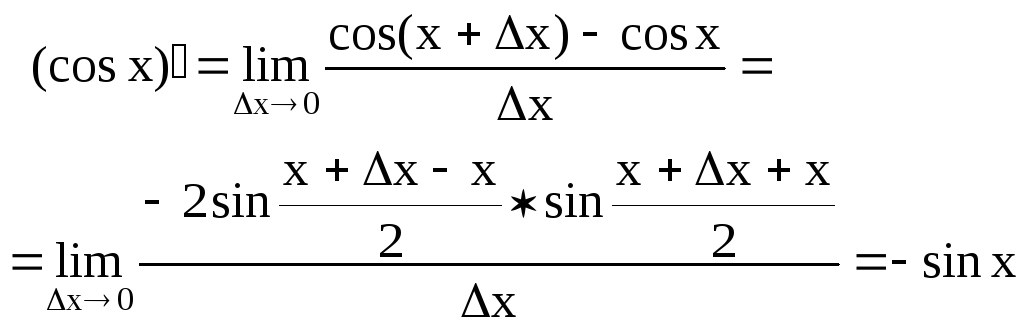
5)
6)
7)
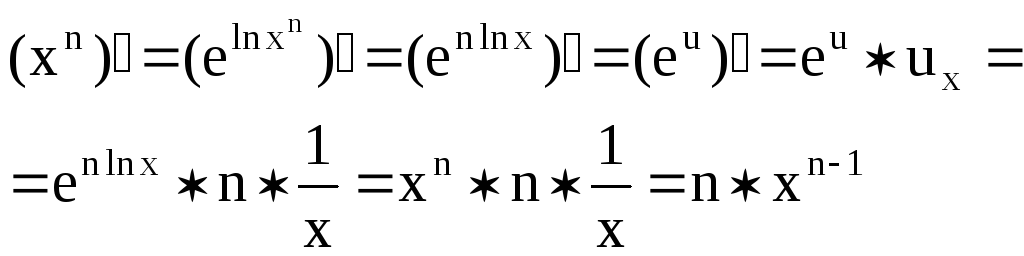
8)
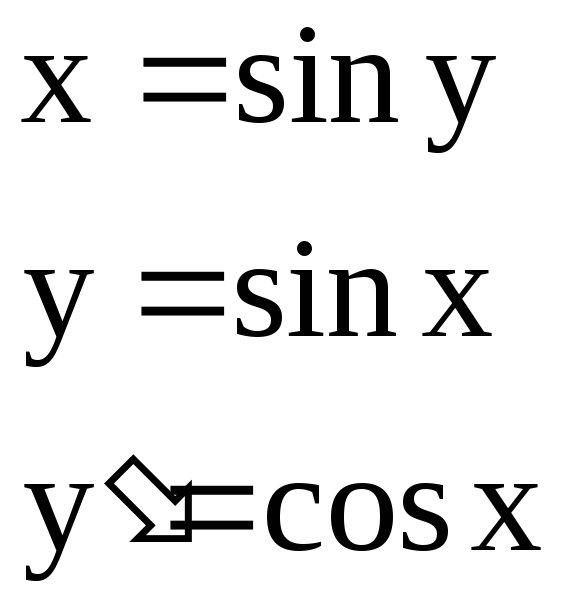
9)
10)
11)
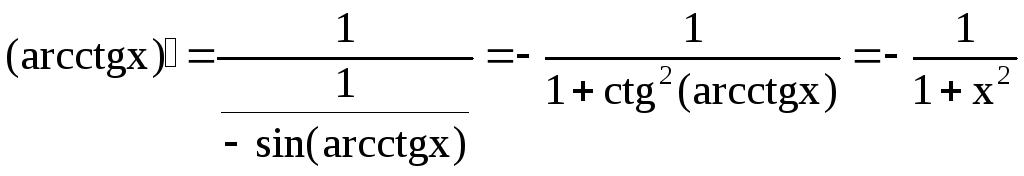
Теорема о производной сложной функции.
Теорема.
Доказательство:
Пусть
,
определена и непрерывна в окрестности
точки (
,
,
определена и непрерывна в окрестности
точки
.
Тогда
.
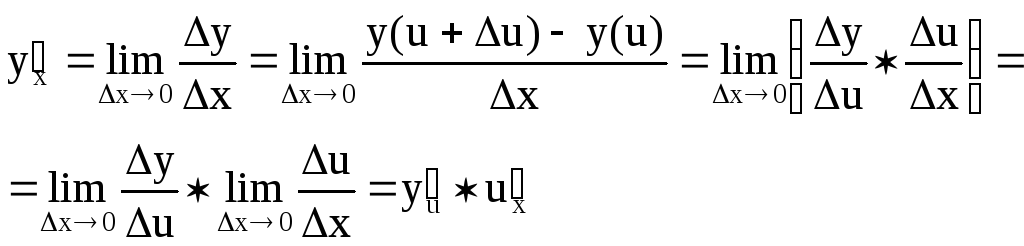
Это верно при условии, что каждая из функций дифференцируема.
Теорема о производной обратной функции.
Теорема.
Доказательство:
Пусть
дифференцируемая в точке (
).
- обратная к
.
Обратная
функция существует если
монотонная функция.
Тогда
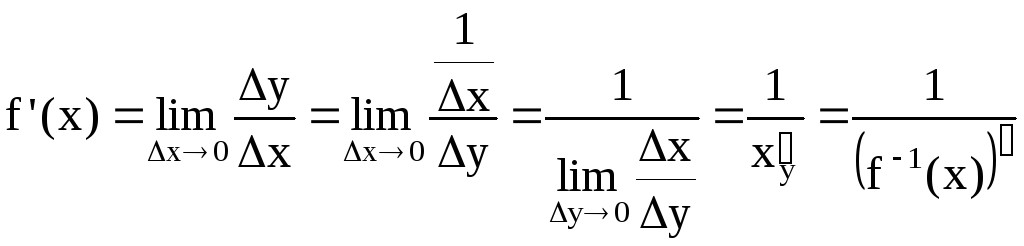
Производная сложной степенной функции.
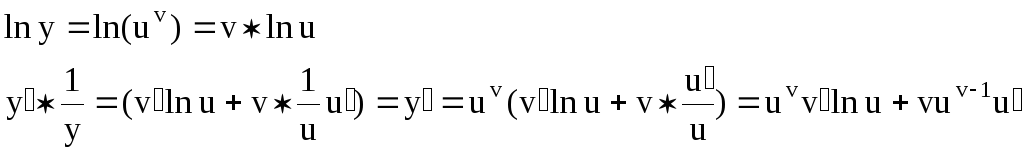
Прием логарифмического дифференцирования.
Производная неявной функции.
– общий вид неявно
заданной функции.
