Тема 2: Основы теории множеств. Диаграммы Эйлера-Венна.

В группе занимается 40 человек. Из них: 20 человек изучают французский язык; 20 человек - английский язык; 14 человек - немецкий язык.

9 человек - английский и французский языки; 7 человек - немецкий и английский; 5 человек - немецкий и французский.

2 человека - все три языка. Сколько человек НЕ изучают НИ одного языка?

Решение:

Для решения задачи построим диаграммы Эйлера-Вена.

Введем обозначения:

А – множество человек, изучающих английский язык;

B – множество человек, изучающих немецкий язык;

C – множество человек, изучающих французский язык

Тогда m(U) = 40, m(A) = 20, m(B) = 14, m(C) = 20.

m() = 9, m()=7, m() = 5.

m() = 2.

Необходимо найти: m() = ?

Проиллюстрируем это на диаграмме:

Тогда:

5 – 2 = 3 – число студентов изучающий только немецкий и французский языки.

14 – 7 – 3 = 4 – число студентов, изучающих только немецкий язык.

20- 9 – 3 = 8 – число студентов, изучающих только французский язык.

20 + 4 + 3 + 8 = 35 – число студентов, которые изучают какие-либо языки.

40 – 35 = 5 = число студентов, вообще не изучает ни одного языка.

Ответ: 5 студентов не изучает ни одного языка.

Тема 3: Основы линейной алгебры. Решение систем линейных уравнений методом Крамера.

Решить систему линейных уравнений методом Крамера:

Решение:

Вычислим определитель матрицы системы уравнений (по правилу треугольника):

Так как , то система имеет единственное решение.

Вычислим определители (разложением по элементам строки или столбца):

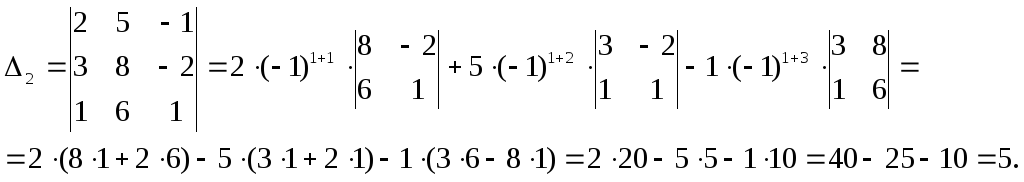
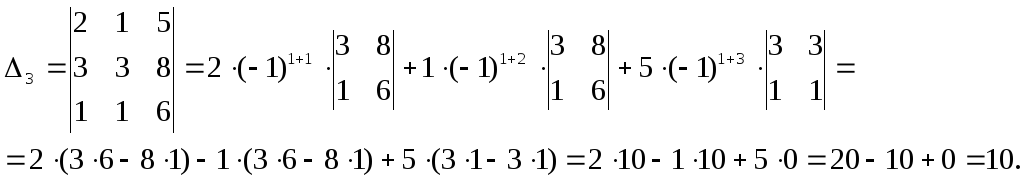
По формулам Крамера находим:

Ответ: х₁=3; х₂=1; х₃=2.

Тема 4: Основы линейной алгебры. Решение систем линейных уравнений матричным методом.

Решить систему линейных уравнений матричным методом:

Решение:

1. Найдем обратную матрицу:

1.1. Найдем определить главной матрицы уравнения:

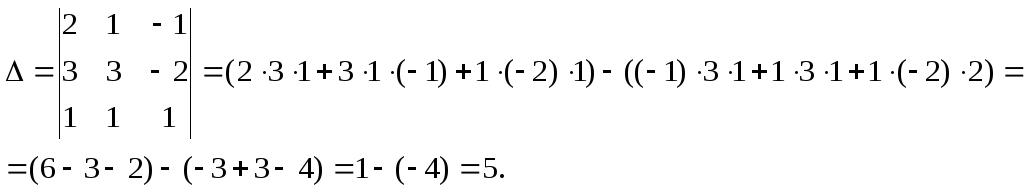
Так как , то делаем вывод, что обратная матрица существует.

1.2. Вычислим алгебраические дополнения для каждого элемента:

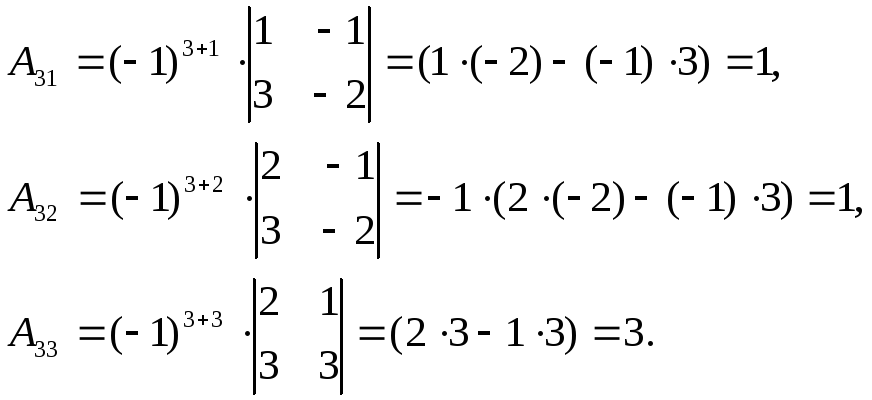
1.3. Составляем матрицу из алгебраических дополнений:

1.4. Транспонируем полученную матрицу:

1.5. Находим обратную матрицу:

2. Найдем :

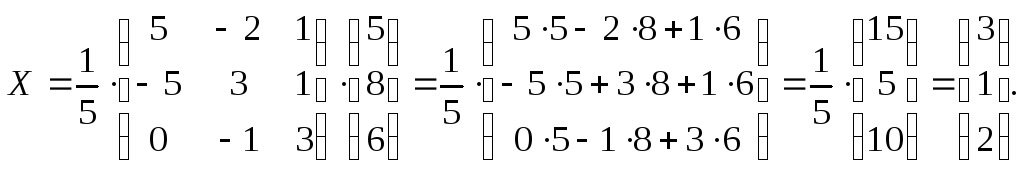
3. Сделаем проверку: :

Ответ:

Тема 5: Математические модели.

При производстве двух видов продукции используется тои вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Задачу решить графическим методом. Исходные данные таковы:

Вид сырья	Запас сырья	Количество единиц сырья, идущих на изготовление единицы продукции
		Р1	Р2
S1	20	2	5
S2	40	8	5
S3	30	5	6
Прибыль от единицы продукции в рублях		50	40

Решение:

Обозначим через х₁ – количество единиц продукции Р₁, а через х₂ - количество едини продукции Р₂. Тогда учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:

,

Которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов, а и , так как количество не может быть отрицательным.

Суммарная прибыль от реализации продукции выразим как .

Таким образом, имеем задачу линейного программирования:

Z=50х1+40х2→max.

Построим многоугольник решений. Для этого в системе координат на плоскости изобразим граничные прямые:

(L₁)

(L₂)

(L₃)

Обозначим штриховкой общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных. Для этого берем какую-нибудь точку не лежащую на граничной прямой (например, О(0,0)), и посмотрим, удовлетворяет ли она неравенствам:

(L₁)

(L₂)

(L₃)

Заштриховываем полуплоскость, которая удовлетворяет неравенствам:

Таким образом, многоугольник ОАВСD – многоугольник решений.

Построим вектор-градиент и через точку О проводим прямую Z, перпендикулярную ему.

Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора .

Из рисунка следует, что наибольшее значение целевой функции Z достигается в точке С, то есть лежит на пересечении прямых L₂ и L₃.

Для определения ее координат решим систему уравнений:

Тогда имеем: и .

Подставляя значения х₁ и х₂ в функцию Z, получаем:

.

Таким образом, чтобы получить максимальную прибыль в размере 260,3 рублей, необходимо запланировать производство 3,9 единицы продукции Р₁ и 1,7 единицы продукции Р₂.

Ответ: ; ; .