
- •Глава 3 Векторная алгебра
- •§ 1. Определение вектора
- •§ 2. Линейные действия над векторами
- •§3. Линейная зависимость векторов. Базис на плоскости и в пространстве
- •§4. Проекция вектора на ось
- •§5. Разложение вектора на составляющие по осям координат
- •§6. Скалярное произведение векторов
- •§7. Векторное произведение векторов
- •§8. Смешанное произведение трех векторов
- •Сводная таблица основных понятий и формул по теме «Векторы»
- •Решение практических задач по теме «Линейные действия над векторами»
- •Решение практических задач по теме «Проекция вектора на ось. Скалярное и векторное произведение»
- •Решение практических задач по теме «Линейная зависимость векторов. Смешанное произведение»
- •Упражнения для самостоятельного решения.
Решение практических задач по теме «Линейные действия над векторами»
П р и м
е
р
1.
Даны координаты
двух
точек А
(1; 0;
–
1) и В
(1;
3;
3). Найти:
1.Координаты вектора
![]() .
.
2. Модуль вектора
![]() .
.
3. Направляющие
косинусы вектора
![]() .
.
4. Синус угла между
вектором
![]() и плоскостью хОу.
и плоскостью хОу.
Решение.
1) Координаты
вектора
![]() найдем с помощью формулы (4):
найдем с помощью формулы (4):
![]() .
.
2) Модуль вектора
![]() вычислим по формуле
вычислим по формуле
![]() .
.
В данной формуле
х,
у,
z
– координаты вектора
![]() .
Следовательно,
.
Следовательно,
![]() .
.
3) Направляющие косинусы можно найти по формулам (3)
![]() .
.
Следовательно,
![]() .
.
4) Синус угла между
вектором
![]() и плоскостью хОу
определим по формуле:
и плоскостью хОу
определим по формуле:
![]() .
.
Ответ:
![]()
Решение практических задач по теме «Проекция вектора на ось. Скалярное и векторное произведение»
П р и м е р 2.
Заданы два вектора
![]() и
и
![]() .
Найти: 1. Координаты векторов
.
Найти: 1. Координаты векторов
![]() и
и
![]() .
.
2. Скалярное
произведение векторов
![]() и
и
![]() .
.
3. Косинус угла
между векторами
![]() и
и
![]() .
.
4. Проекцию вектора
![]() на вектор
на вектор
![]() и проекцию вектора
и проекцию вектора
![]() на вектор
на вектор
![]() .
.
5. Векторное
произведение векторов
![]() и
и
![]() .
.
6. Площадь и высоты
параллелограмма, построенного на
векторах
![]() и
и
![]() .
.
Решение.
1) Координаты векторов
![]() и
и
![]() нетрудно найти, используя формулы (1):
нетрудно найти, используя формулы (1):
![]() .
.
Следовательно,
![]() и
и
![]() .
.
Следует заметить,
что векторы
![]() и
и
![]() геометрически представляют собой
диагонали параллелограмма, построенного
на данных векторах
геометрически представляют собой
диагонали параллелограмма, построенного
на данных векторах
![]() и
и
![]() .
.
2) Скалярное
произведение векторов
![]() и
и
![]() вычислим по формуле (5):
вычислим по формуле (5):
![]()
3) Косинус угла
между векторами
![]() и
и
![]() можно определить с помощью формулы (8)
можно определить с помощью формулы (8)

4) Проекцию вектора
![]() на вектор
на вектор
![]() найдем по формуле (
найдем по формуле (
 .
.
Аналогично вычислим
проекцию вектора
![]() на вектор
на вектор
![]() .
.
 .
.
5) Векторное произведение векторов вычислим по формуле (10):
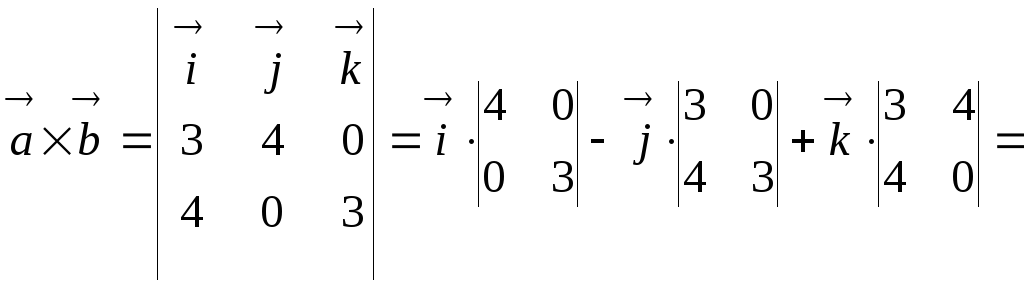
![]()
6) Площадь
параллелограмма, построенного на
векторах
![]() и
и
![]() определим, используя известный
геометрический смысл векторного
произведения. Отсюда искомую площадь
параллелограмма найдем по формуле (9):
определим, используя известный
геометрический смысл векторного
произведения. Отсюда искомую площадь
параллелограмма найдем по формуле (9):
![]() (кв. ед)
(кв. ед)
Ответ: 1)
![]() и
и
![]() ;
;
2) 12; 3) 0,48; 4) 2,4;
5)
![]() ;
6) 21,93 кв. ед.
;
6) 21,93 кв. ед.
Решение практических задач по теме «Линейная зависимость векторов. Смешанное произведение»
Пример 3.
Заданы векторы
![]() ,
,
![]() и
и
![]() .
Требуется:
.
Требуется:
1. Проверить,
компланарны ли векторы
![]() ,
,
![]() ,
,
![]() .
.
2. Проверить,
коллинеарны ли векторы
![]() ,
,
![]() .
.
3. Проверить,
ортогональны ли векторы
![]() и
и
![]() .
.
4. Найти
![]() ,
ортогональный векторам
,
ортогональный векторам
![]() и
и
![]() .
.
5. Объем пирамиды,
построенный на векторах
![]() ,
,
![]() и
и
![]() .
.
6. Вектор
![]() как линейную комбинацию векторов
как линейную комбинацию векторов
![]() ,
,
![]() и
и
![]() .
.
Решение. 1) Компланарность векторов можно проверить с помощью смешанного произведения, т. е. по формуле (12):

![]() .
.
Следовательно
векторы
![]() ,
,
![]() ,
,
![]() не компланарны.
не компланарны.
2) Коллинеарность
векторов проверим по формуле (10), но
сначала найдем координаты векторов
![]() ,
,
![]() по формуле (1):
по формуле (1):
![]() .
.
Аналогично найдем
![]() :
:
![]() .
.
Тогда
 .
.
Следовательно
векторы
![]() ,
,
![]() не коллинеарны.
не коллинеарны.
3)
Ортогональность
векторов
![]() и
и
![]() проверим по формуле (6):
проверим по формуле (6):
![]() .
.
Значит векторы не ортогональны.
4) Найти
![]() ,
ортогональный векторам
,
ортогональный векторам
![]() и
и
![]() можно по формуле:
можно по формуле:
 ,
где
,
где
![]() .
.
Следовательно,
 .
.
5) Объем пирамиды,
построенный на векторах
![]() ,
,
![]() и
и
![]() численно равен абсолютной величине
смешанного произведения этих векторов.
Поэтому
численно равен абсолютной величине
смешанного произведения этих векторов.
Поэтому
![]() .
.
6) Для нахождения
вектора
![]() как линейную комбинацию векторов
как линейную комбинацию векторов
![]() ,
,
![]() и
и
![]() необходимо разложить его по данным
векторам как по базису. То, что векторы
необходимо разложить его по данным
векторам как по базису. То, что векторы
![]() ,
,
![]() и
и
![]() образуют базис, уже показано, так как
смешанное произведение отлично от нуля.
образуют базис, уже показано, так как
смешанное произведение отлично от нуля.
Обозначим неизвестные
координаты вектора
![]() в новом базисе – х,
у,
z.
Тогда для их нахождения имеем следующую
систему уравнений
в новом базисе – х,
у,
z.
Тогда для их нахождения имеем следующую
систему уравнений
 ,
,
где определитель матрицы системы равен 1.
Используем для решения системы уравнений формулу Крамера. Предварительно вычислим определители, полученные путем замены в определители А элементов первого столбца на соответствующие элементы столбца свободных членов рассматриваемой системы:
 ,
,
 ,
,
 .
.
Тогда по формулам Крамера получим:
![]()
или вектор
![]() как линейная комбинация векторов нового
базиса имеет следующий вид
как линейная комбинация векторов нового
базиса имеет следующий вид
![]() .
.
