Решение практических задач по теме: "Параметрические уравнения"

П р и м е р 7. Найти координаты точки на линии, заданной уравнениями x = 2∙t + 3, y = 5∙t, если значение параметра t = 3.

Решение. Подставим значение параметра в уравнения линии и получим точка на плоскости с координатами (9; 15), т. к.

х = 2∙3 + 3 = 9, у = 5∙3 = 15.

П р и м е р 8. Найти уравнение линии в прямоугольной системе координат, если она задана параметрическими уравнениями

.

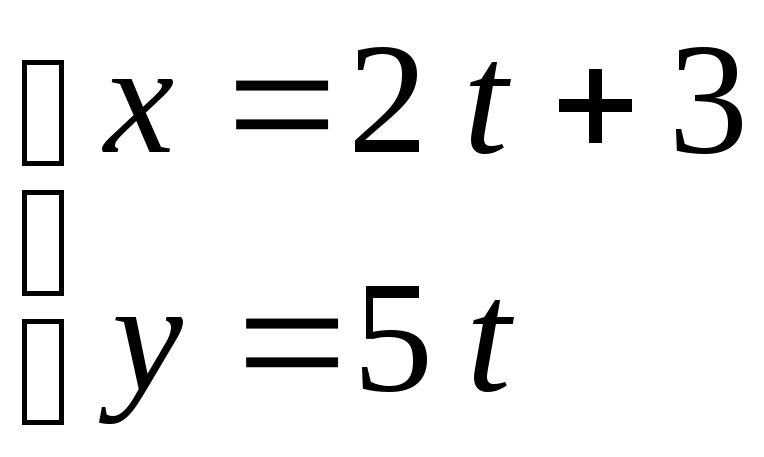Решение. Выразим параметр t из второго уравнения системы и получим . Подставим найденное значение параметра t в первое уравнение и получим искомое уравнение линии

или 5∙х – 2∙у – 15 = 0, т. е. F (x; y) = 0.

Решение практических задач по теме: "Прямоугольные координаты в пространстве"

П р и м е р 9. Построить в пространстве точки: А (4; 3; 5), В (– 2; 4; 3), С (5; – 2; – 2).

Р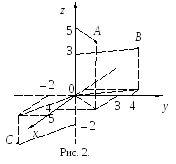ешение. Чтобы построить точку А необходимо на оси абсцисс отложить отрезок равный 4, по оси ординат – отрезок равный 3, по оси аппликат – отрезок равный 5. Затем восстановить перпендикуляры из полученных точек до пересечения друг с другом. Полученная точка и будет точкой А. Аналогично строятся точки В и С (смотри рисунок 2).

Решение практических задач по теме: "Основные задачи на метод координат в пространстве"

П р и м е р 10. Даны точки А (2; 4; – 2) и В (– 2; 4; 2). На прямой АВ найти точку М, делящую отрезок АВ в отношении λ = 3.

Решение. Координаты точки М найдем по формулам (8):

.

Следовательно, искомая точка М (– 1; 4; 1).

Ответ: М (– 1; 4; 1).

П р и м е р 11. Дан треугольник с вершинами А (1;1;1), В (5;1;–2), С (1; – 2; 5). Найти координаты точки пересечения биссектрисы угла А со стороной СВ.

Решение. Найдем длины сторон треугольника, образующих угол А, по формулам (7):

.

.

Следовательно, |CD|:|DB| = 5:5 = 1, так как биссектриса делит сторону СВ на части, пропорциональные прилежащим сторонам. Таким образом, координаты искомой точки найдем по формулам (9) с учетом того, что λ = 1:

.

Ответ: D (3; – 0,5; 1,5).

П р и м е р 12. На оси Ох найти точку, равноудаленную от точек А (2; – 4; 5) и В (– 3; 2; 7).

Решение. Пусть С – искомая точка. Для нее должно выполняться равенство |AC| = |CB|. Так как эта точка лежит на оси Ох, то ее координаты (х; 0; 0), а потому имеем:

,

.

Приравняем |АC| к |ВС| и возведем обе части полученного уравнения в квадрат, т. е.

.

Ответ: С (– 1,7; 0; 0).

Примеры для самостоятельного решения

1. Дана точка А (3; – 2). Найти координаты точек, симметричных точке А относительно оси Ох, оси Оу, начала координат.

2. Построить точки А (– 2; 1) и В (3; 6) и найти точку М (х; у), делящую отрезок АВ в отношении .

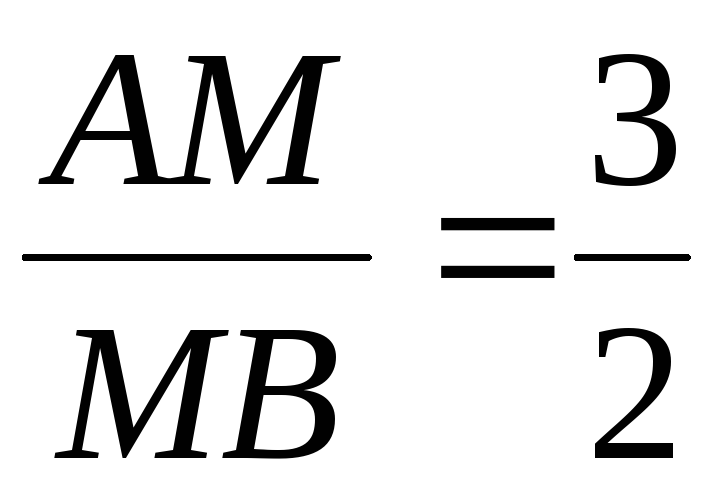3. Определить середины сторон треугольника с вершинами А (2; – 1), В (4; 3), С (– 2; 1).

4. В треугольнике с вершинами А (– 2; 0), В (6; 6), С (1; – 4) определить длину биссектрисы АЕ и медианы АД.

5. В полярной системе координат даны точк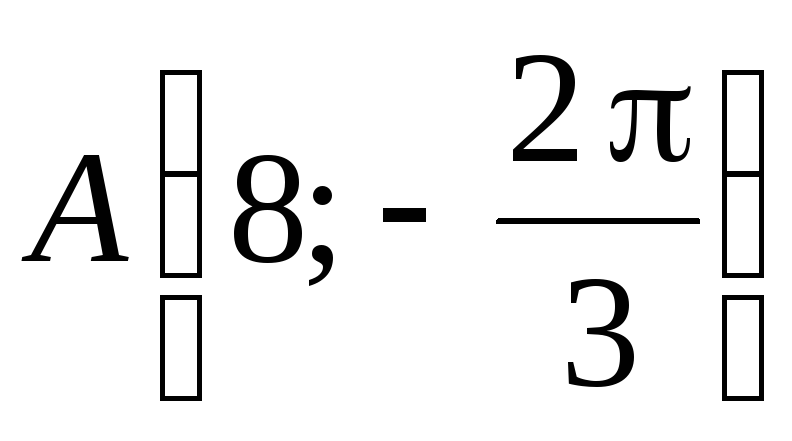и и 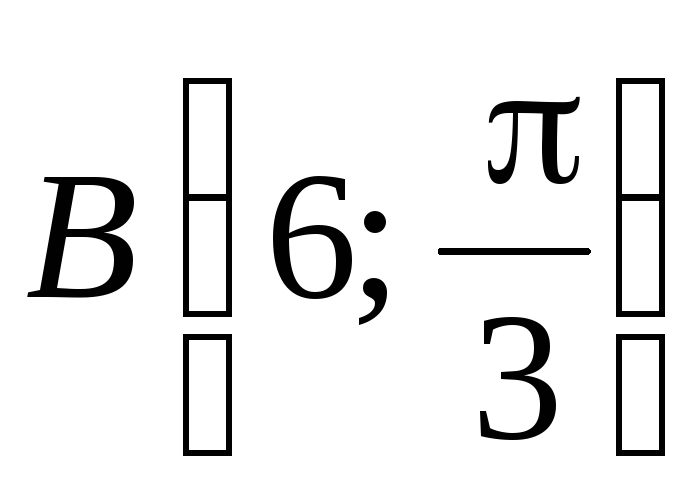. Найти полярные координаты середины отрезка, соединяющего эти точки.

6. Найти площадь треугольника, вершины которого 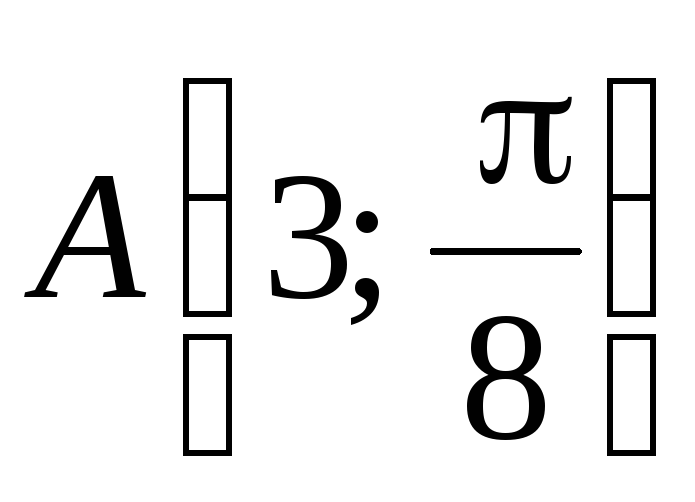, , 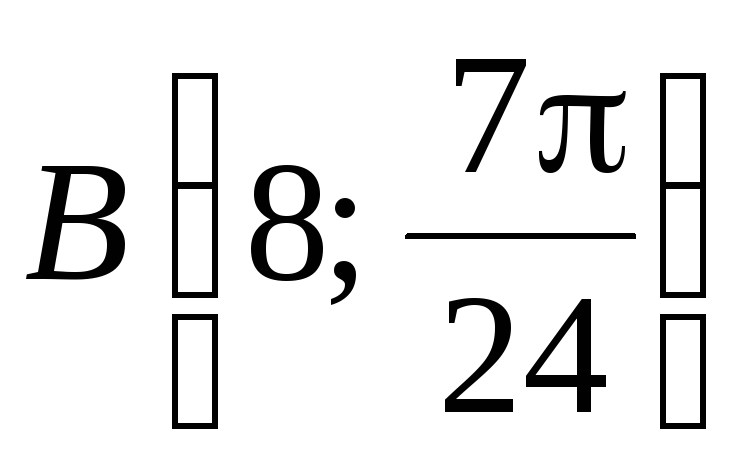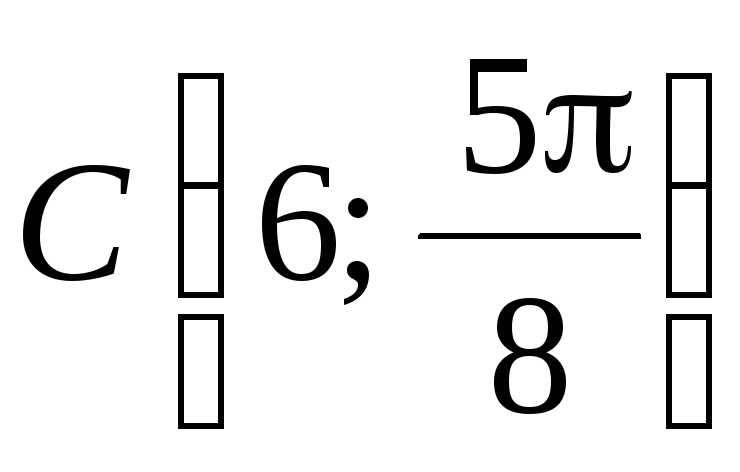заданы в полярных координатах.

7. Построить множество точек плоскости на прямоугольной системе координат, полярные координаты которых удовлетворяют уравнению: а) ρ = 2∙φ; б) ρ = 2∙sin φ; в) ρ∙sin φ = 1; г) tg φ = – 1.

8. В прямоугольных координатах даны параметрические уравнения кривых: а) 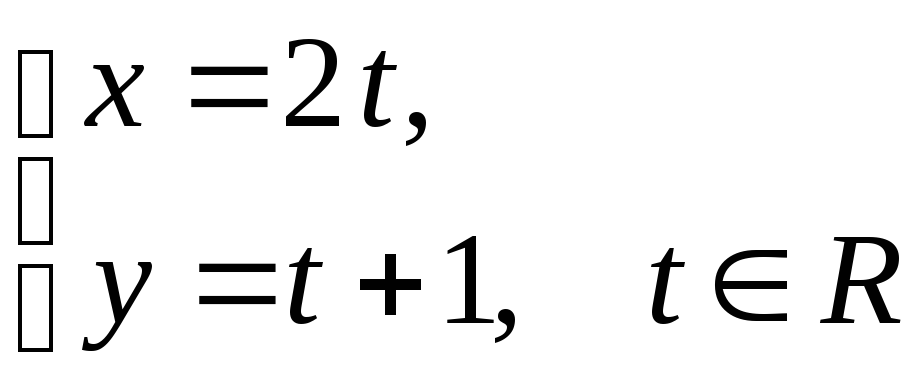; б) Найти уравнения заданных линий в виде F (x; y) = 0.

9. Найти координаты точки на плоскости Оху, равноудаленной от точек А (4; 0; 2), В (– 1; 2; 4), С (1; 1; – 3).

10. Показать, что треугольник с вершинами в точках А (– 3; 2; 4), В (0; – 2; – 1), С (1; 5; 9) равнобедренный.

11. Найти расстояние от точки А (3; – 4; 5) до начала координат и до осей координат.

12. Прямая проходит через точки А (2; – 3) и В (– 6; 5). На этой прямой найти абсциссу точки ордината которой равна (– 5).

13. Проверить, что три данные точки лежат на одной прямой: А (1; – 5; 3), В (5; – 1; 7), С (6; 0; 8).

54