2.2. Распределение Пуассона п()
Случайная величина X имеет распределение Пуассона, если она принимает любые целые неотрицательные значения m = 0,1,2,… с вероятностями
. (2)
Число называется параметром распределения Пуассона. Множество случайных величин, имеющих распределение Пуассона с параметром , будем обозначать П().
Таким образом, X может принимать счетное множество значений, и закон распределения этой случайной величины задается следующей таблицей:
Н
а
рис.4 показаны вероятности P(X
= m)
значений распределения Пуассона при
= 0,5 и
= 2 соответственно.
Р и с. 4. Вероятности значений распределения Пуассона
Распределение Пуассона играет важную роль в физике, теории связи, теории надежности, теории массового обслуживания и т.д. — всюду, где в течение определенного времени может происходить случайное число каких-то событий: радиоактивных распадов, появления метеоритов, телефонных вызовов, помех в каналах связи, отказов оборудования, дорожных происшествий, несчастных случаев и т.д.
Распределение
Пуассона является предельным для
биномиального распределения, если в
схеме Бернулли число испытаний n
стремится к бесконечности, а вероятность
p
появления события
в каждом испытании стремится к нулю,
причем так, что
.
Отсюда получаем приближенную формулу
,
пригодную
для практических расчетов. Этой формулой
рекомендуется пользоваться, если
,
а
.
Для
распределения Пуассона
,
,
.
Пример
3. Вероятность
выпуска дефектного изделия
.
Из продукции выбрано изделий n
= 5000. Найти вероятность того, что среди
них окажется два или более дефектных
изделия.
Параметр
.
Определим требуемую вероятность:
.
Так
как
,
,
искомая вероятность
.
При
точных расчетах,
.
О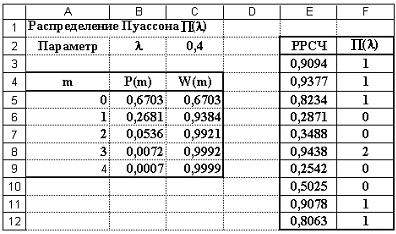
пределение
вероятностей случайной величины X,
подчиненной распределению Пуассона с
параметром
= 0,4, выполненное в Excel,
показано на рис.5.
Р и с. 5. Распределение Пуассона П(0,4)
В ячейке C2 находится значение параметра = 0,4. В ячейках A5:A9 содержатся возможные значения распределения Пуассона: 0, 1, 2, 3, 4; значения 5, 6,… опущены. В ячейках B5:B9 — вероятности этих значений, вычисленные по формуле (2). Так содержимое ячейки B5:
B5 = ПУАССОН(A5;$C$2;ЛОЖЬ).
Ячейки C5:C9 содержат накопленные суммы вероятностей, а именно, C5 = B5, C6 = C5 + B6, C7 = C6 + B7, и т.д.
Разыгрывание случайной величины, подчиненной распределению Пуассона, производится по формуле:
где
— равномерно распределенное случайное
число из промежутка [0;1]. Например, чтобы
получить 10 значений случайной величины,
надо в ячейку E3
записать СЛЧИС(), а в ячейку F3
— формулу
= ЕСЛИ(E3<$C$5;$A$5;ЕСЛИ(E3<$C$6;$A$6;ЕСЛИ(E3<$C$7;
$A$7;ЕСЛИ(E3<$C$8;$A$8;$A$9)))).
После копирования содержимого пары ячеек E3:F3 на блок E4:F12 в ячейках F3:F12 получим 10 значений случайной величины, имеющей распределение Пуассона.
2.3. Геометрическое распределение g(p)
Вероятность
появления события
в одном испытании равна p.
Производится серия из нескольких
независимых испытаний, в каждом из
которых может появиться или не появиться
событие
.
Испытания продолжаются до тех пор, пока
не появится событие
.
Случайная величина X,
равная числу испытаний до первого
появления события
,
имеет геометрическое
распределение
вероятностей.
Очевидно,
что случайная величина X
может принять одно из значений m
= 1, 2, 3,…. Значение X
равно m,
если в m-1
- м испытании событие
не произойдет, а в m
- м испытании событие
произойдет. Поэтому
. (3)
Множество случайных величин, имеющих геометрическое распределение с параметром p, обозначается G(p).
Для геометрического распределения
,
,
.
Пример
4. В магазине
покупатель выбирает компьютер до тех
пор, пока не найдет наиболее подходящий.
Вероятность того, что ему понравится
компьютер, составляет
.
Требуется составить таблицу распределения
вероятностей случайной величины X,
равной числу компьютеров, просмотренных
покупателем.
Очевидно,
что случайная величина X
имеет геометрическое распределение
вероятностей. Она может принимать
значения 1, 2, 3,…. Так как
,
то по формуле (3) вероятности этих
значений:
;
;
;
и т.д. В результате получим таблицу распределения вероятностей:
-
X
1
2
3
…
P
0,3
0,21
0,147
…
Геометрическое распределение G(p) определяется одним параметром p. Фрагмент таблицы этого распределения, выполненный в Excel, представлен на рис.6.
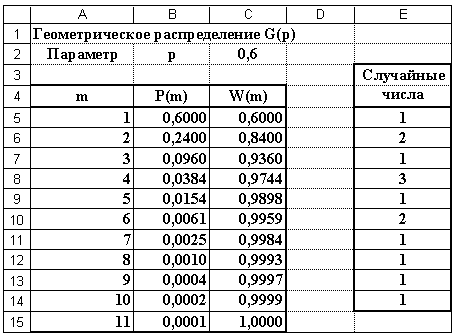
Р и с. 6. Геометрическое распределение G(0,6)
В ячейке C2 находится значение параметра p, равное 0,6. В ячейках A5:A15 содержатся возможные значения геометрического распределения, в ячейках B5:B15 — вероятности этих значений, вычисленные по формуле (3). Так, содержимое ячейки B5:
B5 = $C$2*(1 - $C$2)^(A5 - 1).
Ячейки C5:C15 содержат накопленные суммы вероятностей, а именно: C5 = B5, C6 = C5 + B6, C7 = C6 + B7, и т.д.
Для разыгрывания случайной величины, подчиненной геометрическому распределению, применяется формула
,
где
— равномерно распределенное случайное
число из промежутка [0;1]. Например, чтобы
получить 10 значений случайной величины,
надо в ячейке E5
записать формулу
E5 = ЦЕЛОЕ(LN(СЛЧИС()) / LN(1 - $C$2)) + 1
и скопировать ее в ячейки E6:E14.