Министерство образования и науки рф

________________________________________________________________________________________

Государственное образовательное учреждение высшего профессионального образования

«Санкт-Петербургская государственная лесотехническая академия имени С.М.Кирова»

Кафедра математических методов и моделирования в экономике и управлении

Лабораторная работа№6 По дисциплине : «Математическое моделирование лесных экосистем».

Выполнила: студентка

ЛХФ 5курса 1 маг

Зачетная книжка№507043

Болдышевич А.А

Проверил: доктор технических наук, профессор

Гуров С.В

Санкт-Петербург

2012год

ОПТИМИЗАЦИЯ ПЛАНА ВЫПУСКА ПРОДУКЦИИ ПО ДВУМ КРИТЕРИЯМ

1. Постановка задачи

На лесоперерабатывающем предприятии установлено три группы оборудования , и (строгальные, фрезерные и шлифовальные станки). Эти станки производят два типа продукции и . Известны нормы затрат машинного времени, эффективный фонд времени станков, цена за простой единицы оборудования и прибыль от реализации единицы продукции (табл. 1).

Таблица 1

Оборудование	Затраты машинного времени на обработку единицы продукции, ч		Эффективный фонд времени станков, ч	Цена за простой единицы оборудования, ден.ед.
Прибыль от реализации единицы продукции, ден.ед.

Определить количество продукции и , которое необходимо изготовить на предприятии с тем, чтобы,

• во-первых, получить наибольшую общую прибыль от реализации готовой продукции и,

• во-вторых, наиболее эффективно использовать имеющееся оборудование.

Для выполнения работы необходимо

1. Составить математическую модель в виде двухкритериальной задачи оптимизации.

2. Построить допустимую область задачи. Определить оптимальное решение по каждому критерию графическим методом.

3. Построить множество достижимости и множество Парето. Указать множество Парето-оптимальных точек.

4. Решить задачу отдельно по каждому критерию в Excel.

5. Определить компромиссное решение задачи методом уступок. Величину уступки принять равной половине разности между значениями прибыли, полученными в результате оптимизации по каждому критерию.

6. Показать, что компромиссное решение является эффективным по Парето.

2.Выполнения лабораторной работы Исходные данные в табл.2.

Таблица 2

Оборудование	Затраты машинного времени на обработку единицы продукции, ч		Эффективный фонд времени станков, ч	Цена за простой единицы оборудования, ден.ед.
	10	5	440	3,2
	1	26	962	3,2
	26	6	962	4,5
Прибыль от реализации единицы продукции, ден.ед.	20	7

Составим математическую модель. Пусть

и – количество продукции и , которую необходимо изготовить на предприятии,

– общая прибыль от реализации готовой продукции,

– суммарные издержки (штраф) предприятия за простой оборудования.

Фактическая загрузка по каждой группе оборудования равна: – для фрезерных станков, – для сверлильных станков, – для шлифовальных станков. Коэффициенты при неизвестных обозначают здесь нормы затрат машинного времени на обработку единицы продукции и . Загрузка по каждой группе оборудования не должна превышать фонда машинного времени, т.е.:

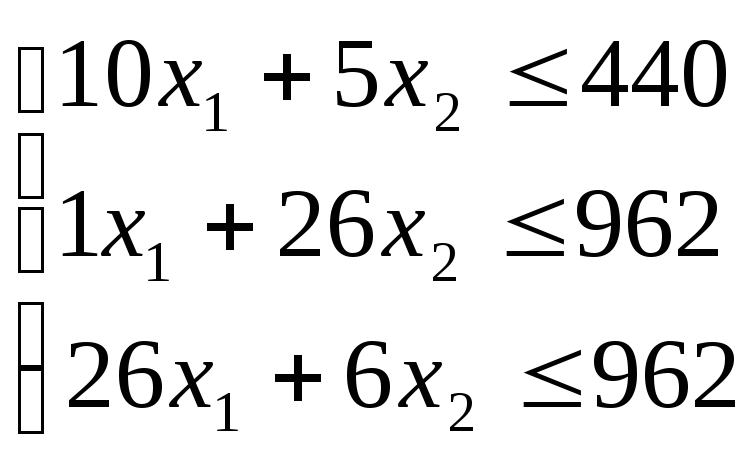. (1)

Неизвестные, очевидно, должны быть неотрицательными:

, . (2)

Неравенства (1) и (2) образуют систему ограничений. Представим аналитически цели задачи. Общая прибыль от реализации готовой продукции (цель 1) выражается формулой

. (3)

Из ограничений (1) следует, что время простоя оборудования равно:

– для фрезерных станков,

– для сверлильных станков,

– для шлифовальных станков,

поэтому суммарные издержки предприятия за простой оборудования (цель 2) составляют:

z₂=3,2(440-10x₁-5x₂)+3,2(962-1x₁-26x₂)+4,5(962-26x₁-6x₂),

или

Таким образом, математическая модель задачи состоит в максимизации целевой функции (3) и минимизации целевой функции (4) при условиях, что неизвестные и удовлетворяют системе ограничений (1) и неравенствам (2). Это есть задача линейной оптимизации с двумя критериями.

На рис. 1 приведено графическое решение задачи по каждому критерию в отдельности. На основе системы ограничений (1) – (2) строим допустимую область в виде многоугольника OABCD. Построение прямой I: в уравнении положим , тогда получим . Затем , тогда . Через эти точки проводим прямую I. Неравенство определяет полуплоскость, расположенную ниже этой прямой. Аналогично неравенство задает полуплоскость, расположенную под прямой II, а неравенство – полуплоскость, расположенную левее прямой III. Условия неотрицательности (2) в совокупности определяют первый квадрант координатной плоскости.

Оптимальное решение задачи по первому критерию определяется следующим образом. Строится вектор , координаты которого равны (или пропорциональны) коэффициентам целевой функции (3). Перпендикулярно этому вектору изображается прямая (линия уровня целевой функции), которая перемещается в направлении вектора, пока прямая имеет общие точки с допустимой областью. Оптимальное решение по первому критерию есть точка пересечения допустимой области с линией уровня, отвечающей максимальному значению . Это есть вершина С. Координаты точки определяются по графику приближенно. Они дают оптимальное решение задачи по первому критерию.

p1(40;14)

p2(38,1;31,6)

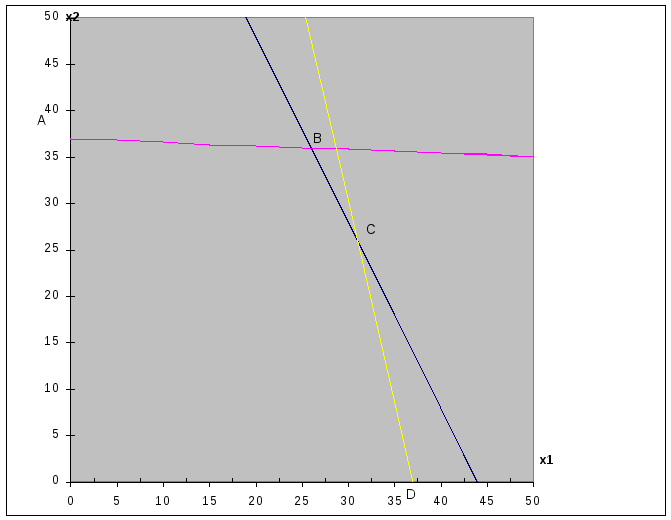
Рис. 1. Графическое решение задачи по первому и второму критериям

Оптимальное решение задачи по второму критерию определяется аналогично, если задачу минимизации (4) заменить задачей максимизации целевой функции и построить вектор , координаты которого пропорциональны координатам вектора . Из рисунка видно, что оптимальной точкой является вершина .

Таким образом, выпуск продукции и в количествах 31 и 26 единица обеспечивает предприятию максимальную общую прибыль, а выпуск продукции и в количествах 26 и 36 единицы гарантирует предприятию минимальный общий штраф за простой оборудования. Для построение допустимой области в соответствии с уравнениями системы (1) образуем табл. 3. В блок ячеек A3 : A14 введем значения аргумента , изменяющегося от нуля до . Таблица 3

x1	x2
	Прямая I	Прямая II	Прямая III
0	88	37,00	160,33
5	78	36,81	138,67
10	68	36,62	117,00
15	58	36,42	95,33
20	48	36,23	73,67
25	38	36,04	52,00
30	28	35,85	30,33
35	18	35,65	8,67
40	8	35,46	-13,00
45	-2	35,27	-34,67
50	-12	35,08	-56,33
55	-22	34,88	-78,00
60	-32	34,69	-99,67
65	-42	34,50	-121,33
70	-52	34,31	-143,00
75	-62	34,12	-164,67
80	-72	33,92	-186,33
85	-82	33,73	-208,00
90	-92	33,54	-229,67
95	-102	33,35	-251,33
100	-112	33,15	-273,00
105	-122	32,96	-294,67
110	-132	32,77	-316,33
115	-142	32,58	-338,00
120	-152	32,38	-359,67
125	-162	32,19	-381,33
130	-172	32,00	-403,00
135	-182	31,81	-424,67
140	-192	31,62	-446,33
145	-202	31,42	-468,00
150	-212	31,23	-489,67
155	-222	31,04	-511,33
160	-232	30,85	-533,00

В ячейки B3, C3 и D3 введем формулы из табл. 4, которые копируются на блок ячеек B4 : D14.

Таблица 4

B3	= (440 – 10 * A3) / 5
C3	= (962 – 1 * A3) / 26
D3	= (962 – 26 * A3) / 6

С помощью мастера диаграмм и блока ячеек B3 : D14 из табл. 3 строятся графики прямых линий I, II и III.

Затем,строим множество достижимости. Это есть образ многоугольника OABCD при отображении и . Составим для этого табл. 5.

Таблица 5

A	B	C	D	E	F
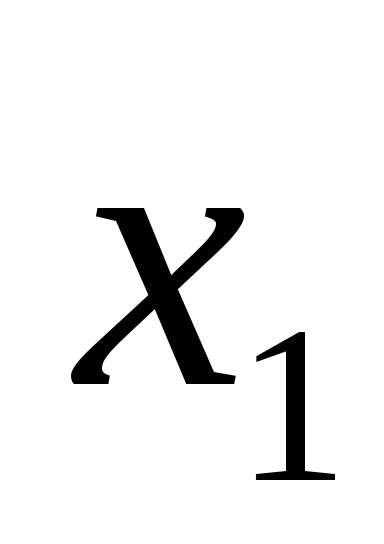
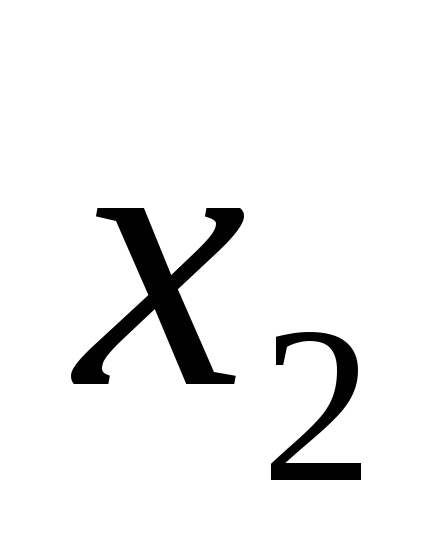
вершина допустимой области			вершина множества достяжимости
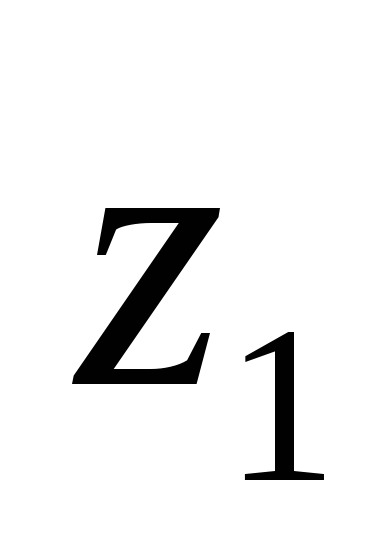
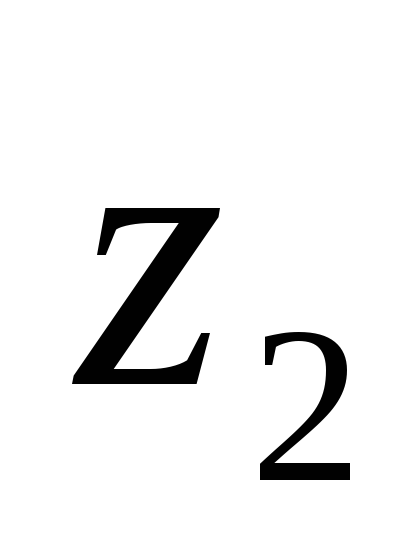
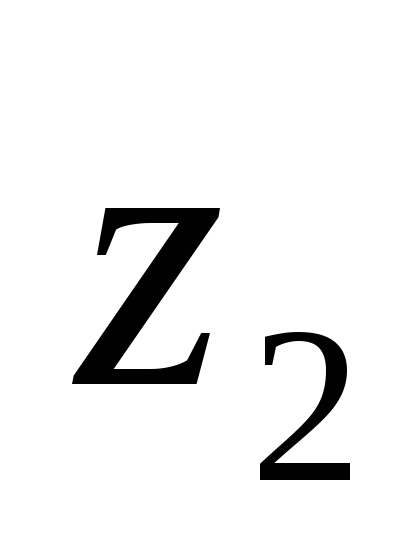
O	0	0	O´	0	8815,4
A	0	37	A´	259	4146
B	26	36	B´	772	315
C	31	26	C´	802	816
D	37	0	D´	740	3184
			O´	0	8815,4

В колонках A, B и C вписаны обозначения вершин допустимой области и их координаты. В колонках D, E и F находятся обозначения вершин множества достижимости и их координаты, рассчитанные по целевым функциям (3) – (4): в ячейки E22 и F22 заносятся формулы из табл. 1.6, которые копируются на блок ячеек E23 : F26.

Таблица 6

E22	= 20 * B22 + 7 * C22
F22	= – 152,2 * B22 – 126,2 * C22 + 8815,4

Начальная вершина O´ со своими координатами повторяется в строке 27. На плоскости по данным табл. 5 строится множество достижимости, как показано на рис. 2.

Множество Парето образует юго-восточную границу множества достижимости, поскольку и . В данном случае множество Парето есть отрезок B´C´.

Это значит, что точки отрезка BC на рис. 1 образуют множество Парето – оптимальных (или эффективных) точек.

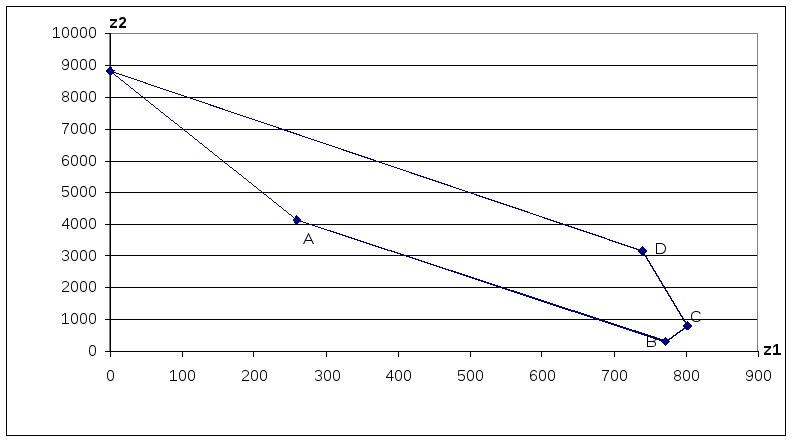
Рис. 2. Множество достижимости и множество Парето

Организация данных для решения задачи по первому критерию представлена в табл. 7.

Таблица 7

	A	B	C	D	E	F	G
1	Целевая функция 1 – прибыль от реализации готовой продукции
2
3	Продукция	P1	P2
4	Значение	31	26
5					Ограничения
6	Станки			Левая часть	Знак	Правая часть	Штраф
7	Фрезерные	10	5	440	<=	440	3,2
8	Сверлильные	1	26	707	<=	962	3,2
9	Шлифовальные	26	6	962	<=	962	4,5
10				ЦФ1->max		ЦФ2	816
11	Прибыль	20	7	802

Вначале ячейки B4 : C4 – пустые, они предназначены для записи решения задачи. В ячейках D7 и G10 записаны формулы из табл. 8. Содержимое ячеек D8, D9, D11 получено копированием формулы из D7.

Таблица 8

D7	= СУММПРОИЗВ(B7 : C7; $B$4 : $C$4)
G10	= СУММПРОИЗВ(G7 : G9; F7 : F9 – D7 : D9)

Далее идет обращение к процедуре «Поиск решения» в пункте меню «Сервис». Целевой ячейкой является D11. Оптимальный план выпуска продукции и в количествах 31 и 26 единица содержится в ячейках B4 : C4, максимальная прибыль (ячейка D11) равна 802ден.ед, штраф за простой оборудования (ячейка G10) – 816 ден.ед.

Решение задачи по второму критерию выполняется на другом листе аналогично (см. табл. 9), но целевой ячейкой служит G10.

Таблица 9

	A	B	C	D	E	F	G
1	Целевая функция 2 – прибыль от реализации готовой продукции
2
3	Продукция	P1	P2
4	Значение	26	36
5					Ограничения
6	Станки			Левая часть	Знак	Правая часть	Штраф
7	Фрезерные	10	5	440	<=	440	3,2
8	Сверлильные	1	26	962	<=	962	3,2
9	Шлифовальные	26	6	892	<=	962	4,5
10				ЦФ1		ЦФ2->min	315
11	Прибыль	20	7	772

Оптимальное решение по второму критерию (ячейки B4 : C4) состоит в выпуске продукции и в количествах 26 и 36 единицы, минимальный штраф за простой оборудования (ячейка G10) составляет 315 ден.ед., прибыль (ячейка D11) равна 772 ден.ед.

Компромиссное решение задачи определяется на третьем листе методом уступок. Согласно условию величина уступки принимается равной . Организация данных представлена в табл. 10. Целевая ячейка – G11.

Таблица 10

Решение задачи МКО методом уступок
Продукция	P1	P2
Значение	29	30
				Ограничения
Станки			Левая часть	Знак	Правая часть	Штраф
Фрезерные	10	5	440	<=	440	3,2
Сверлильные	1	26	809	<=	962	3,2
Шлифовальные	26	6	934	<=	962	4,5
Прибыль	20	7	790	>=	787
					ЦФ2->min	615,6

Полученные результаты оптимизации сведены в табл. 11.

Таблица 11

Критерий оптимальности		Продукция						Значения целевых функций
	Точка на рис.1		P1		P2		Точка на рис.2		z1, ден.ед.	z2, ден.ед.
Прибыль от реализации продукции		C		31		26		C´	802		816
Штраф за простой станков		B		26		36		B´	772		315
Компромиссное решение		K		29		30		K´	790		615,6

Компромиссное решение (ячейки B4 : C4) состоит в выпуске продукции и в количествах 29 и 30 единицы. Оно обеспечивает предприятию высокую (но не максимальную) общую прибыль, равную 790 ден.ед., но при этом штраф за простой оборудования уменьшится и составит 615,6 вместо 816 ден.ед.

Множество точек,есть отрезок BC с уравнением . Поскольку , то компромиссное решение (точка К на рис.1) удовлетворяет этому уравнению и, значит, является эффективным по Парето.