мой гот 3

Министерство образования и науки РФ

________________________________________________________________________________________

Государственное образовательное учреждение высшего профессионального образования

«Санкт-Петербургская государственная лесотехническая академия имени С.М.Кирова»

Кафедра математических методов и моделирования в экономике и управлении

Лабораторная работа№3

По дисциплине : «Математическое моделирование лесных экосистем».

Выполнила: студентка

ЛХФ 5курса 1 маг

Зачетная книжка№507043

Болдышевич А.А

Проверил: доктор технических наук, профессор

Гуров С.В

Санкт-Петербург

2012год

Лабораторная работа 3

МОДЕЛИРОВАНИЕ РОСТА ДРЕВОСТОЯ

1. Постановка задачи

На некотором лесном массиве в момент времени запас древостоя характеризуется величиной . Требуется определить запас древостоя при для двух случаев:

• относительная скорость прироста запаса древостоя обратно пропорциональна текущему времени с коэффициентом пропорциональности (свободный рост древостоя),

• относительная скорость прироста запаса древостоя обратно пропорциональна времени и линейно убывает с увеличением его запаса, т. е. она равна величине 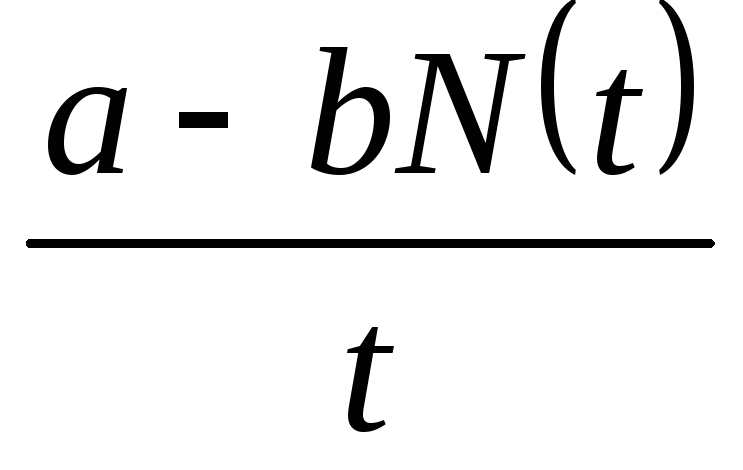(ограниченный рост древостоя).

Для этого необходимо

• составить математическую модель свободного роста древостоя в виде линейного дифференциального уравнения, найти аналитическое решение полученного уравнения;

• составить математическую модель ограниченного роста древостоя в виде дифференциального уравнения Бернулли, определить аналитическое и численное решение уравнения при заданных начальных условиях, приближенное совпадение полученных решений показать графически;

• привести графическую иллюстрацию изменения запаса для моделей свободного и ограниченного роста древостоя;

• сделать выводы по работе.

2. Сведения из теории

Предположим, что скорость изменения древостоя пропорциональна имеющемуся запасу и обратно пропорциональна текущему времени. Обозначим – запас древостоя на некотором участке леса в момент времени . Тогда математическая модель представляется дифференциальным уравнением

, (1)

где – некоторый коэффициент пропорциональности.

Это частный случай модели Мальтуса, когда коэффициент рождаемости , а коэффициент смертности .

Общим решением этого уравнения является степенная функция

.

Исходя из начального условия , получим, что , откуда . Следовательно, частное решение, удовлетворяющее начальному условию, имеет вид

, при . (2)

Уравнение (1) представляет собой математическую модель свободного или неограниченного роста древостоя. Очевидно, что с течением времени запас древостоя, рассчитанный по формуле (2), неограниченно возрастает, что противоречит действительности.

Более точная математическая модель получается в предположении, что относительная скорость изменения запаса древостоя линейно убывает с увеличением его запаса и обратно пропорциональна текущему времени. Тогда

. (3)

Уравнение (3) является частным случаем дифференциального уравнения Бернулли. Его решение можно определить с помощью замены переменных . Тогда получим

,

или

.

Таким образом, уравнение (3) свелось к линейному дифференциальному уравнению. Общим решением последнего уравнения является функция , в чем легко убедиться путем непосредственной подстановки. Следовательно, общим решением уравнения (3) является функция

.

Учитывая начальное условие получим, что . Тогда частным решением уравнения (3), которое удовлетворяет начальному условию, является функция

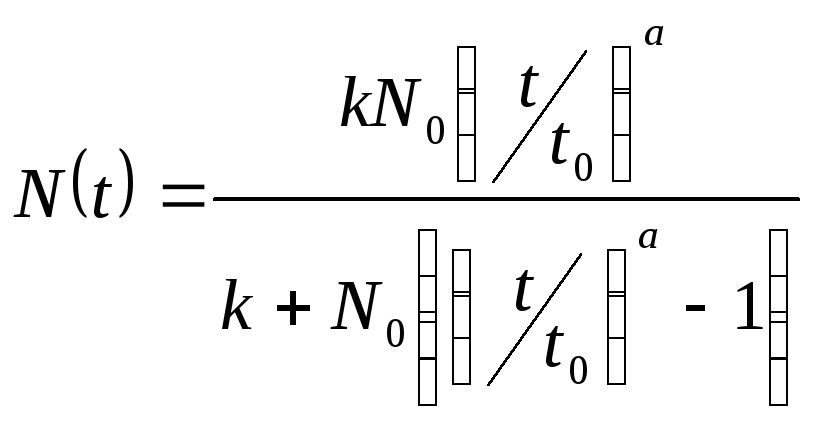при . (4)

Это случай ограниченного роста древостоя. При получим , монотонно возрастая.

Численное решение уравнения (3) определим в Excel методом Эйлера. Запишем уравнение (3) в общем виде

,

где правая часть имеет вид .

Выберем достаточно малый шаг интегрирования и пусть , , , - узлы интегрирования. На основе начального условия имеем , а значения искомой функции , ,…, в узлах определяются по рекуррентным формулам

,

,

…,

. (5)

В результате будет получена таблица значений искомой функции в узлах интегрирования.

Графики функций (2) и (4), соответствующих случаям неограниченного и ограниченного роста запасов древостоя, изображены на рис.1 для значений , и начальных условий , .

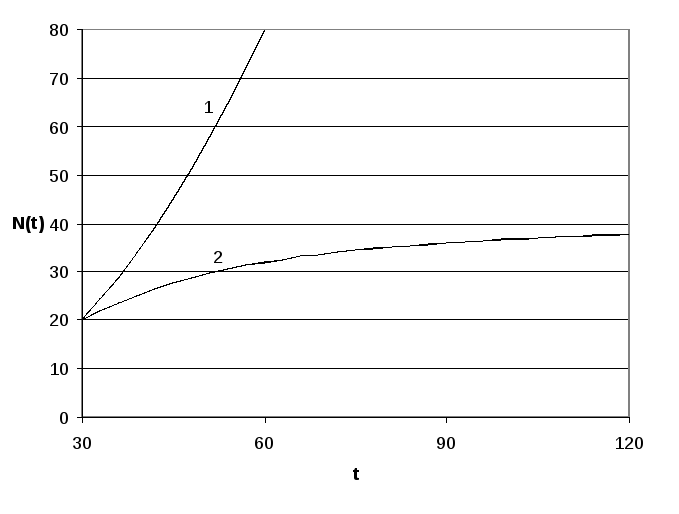
Рис.1. Запас древостоя для свободного (кривая 1) и ограниченного (кривая 2) роста

Из рисунка следует неограниченное возрастание кривой 1, соответствующей функции (2). График функции (4) имеет ярко выраженную горизонтальную асимптоту, соответствующую предельному значению запаса древостоя .

3. Выполнения лабораторной работы

. Исходные данные Excel в виде табл.1.

Таблица 1

, час	N0		k
12	51	1,52	82

1. Неограниченный рост запаса древостоя

Дифференциальное уравнение (1) представляет собой математическую модель неограниченного роста запаса древостоя. Его частным решением, удовлетворяющим начальному условию , является функция, полученная из (2), вычисленная для параметров табл.1

, при . (6)

2. Ограниченный рост запаса древостоя

Дифференциальное уравнение (3) является математической моделью ограниченного роста запаса древостоя. Аналитическое решение этого уравнения следует из соотношения (4). Для заданного начального условия получим решение в виде

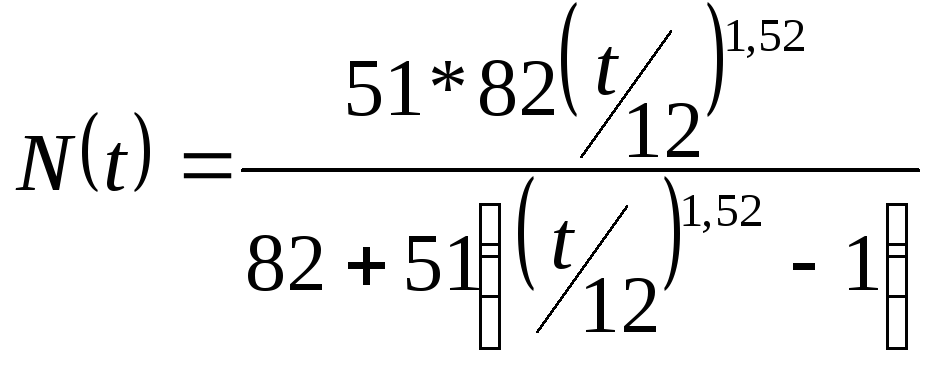. (7)

Численное решение определим методом Эйлера. Поместим в ячейку H2 значение шага интегрирования , который примем равным 0,1.

Последующие результаты расчетов представим в виде табл.2.

Таблица 2

	A	B	C	D	E
1	t	Вспом.функ.	неогр рост	огр рост	Эйлер
2	12	1	51	51	51
3	12,1	1,0126941	51,647398	51,24283	51,24421951
4	12,2	1,0254428	52,297584	51,48291	51,48566328
...	…	…	…	…	...
1000	111,8	29,735555	1516,5133	80,35736	80,37481419
1001	111,9	29,775992	1518,5756	80,35955	80,37697995
1002	112	29,816448	1520,6388	80,36173	80,37914095

В табл.2 время изменяется от час. до час. с шагом . Соответствующие значения содержатся в блоке ячеек A2 : A1002. В столбце B содержатся значения вспомогательной функции . В столбце C содержатся значения функции (6), соответствующие свободному росту запаса древостоя, в столбцах D и E содержатся значения, соответствующие ограниченному росту запаса древостоя на основе аналитического решения (7) и численного алгоритма (5). Для этого в ячейки B2, C2 и D2 следует поместить формулы из табл.3

Таблица 3

B2	= СТЕПЕНЬ(A2 / 12, 1,52)
C2	= 51 * В2
D2	= 51*82* B2 / (82 + 51 * (B2 - 1))

Указанные формулы протягиваются на ячейки B3 : B1002, C3 : C1002 и D3 : D1002 соответственно.

В ячейку E2 помещается значение . Согласно алгоритму (5) в ячейку E3 помещается формула

= E2 + $H$2 * 1,52/А2 * E2 * (1 – E2 / 82),

которая копируется на блок ячеек E4 : E1002.

Установим близость аналитического и численного решений дифференциального уравнения (3), соответствующего ограниченному росту запаса древостоя. Для этого построим графики изменения запаса по колонкам D и E (см. рис.2).

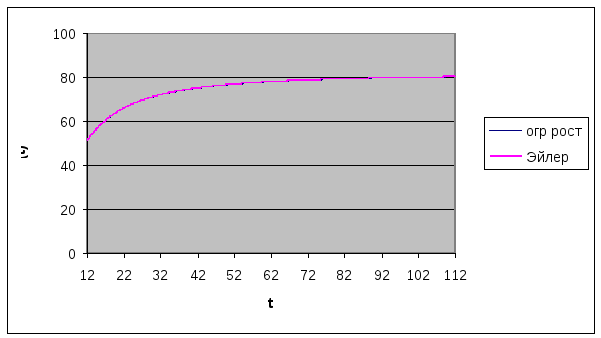
Рис.2. Графики аналитического и численного решений уравнения (3)

Из рис.2 следует практическое совпадение решений дифференциального уравнения аналитическим и численным методами.

3. Иллюстрация изменения запаса древостоя для неограниченного и ограниченного роста

На рис. 3 представлены графики неограниченного и ограниченного роста запаса древостоя на основе данных колонок C и D.

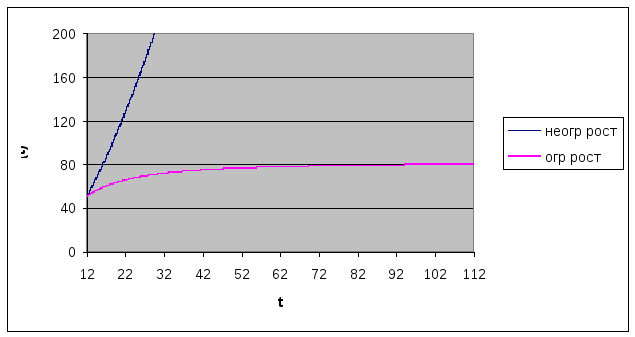
Рис. 3. Кривая 1 – неограниченный, кривая 2 – ограниченный роста древостоя

График ограничен сверху горизонтальной линией, соответствующей запасу .

Из рисунка следует неограниченный рост запаса древостоя для первого случая и ограниченный рост для второго случая. В случае ограниченного роста кривая изменения запаса древостоя входит в стационарный режим, приближаясь к предельному значению k=82.