Кзп в неоднородном поле

Сформируем неоднородное поле, плотность которого линейно возрастает по обеим координатам (x, y) = kxy (рис. 2.5 б):

>> x=sqrt(rand(1,70))*10;y=sqrt(rand(1,70))*10;plot(x,y,'.'),grid on

Коэффициент k в законе изменения плотности найдем из соотношения 70 = k 10²10²/4: k = 0,028. Для вычисления параметра a = _iS_i = kx_iy_iS_i нужно знать координаты центра x_i, y_i и площадь каждого УА. Второй выходной параметр метода PolyRect\Area – массив площадей элементов, координаты центров можно получить методом PolyRect\Center:

>> [S,Si]=Area(T1), Ci=Center(T1)

S = 6.4500 Si = 1.5000 1.5000 0.7500 0.9000 0.9000 0.9000

Ci = 5.0000 3.5000 6.1250 6.8000 3.5000 3.5000

5.0000 5.0000 5.0000 5.0000 3.7500 6.2500

Вероятности поражения УА зададим вектором p, и вычислим вероятность поражения цели по формулам (2.16), (2.17):

>> p=[0.4 0.5 0.3 0.6 0.6 0.8]; K=0.028; G1=1-exp( -K*dot(prod(Ci),Si.*p))

G1 = 0.8816

Вероятности поражения цели еще в двух позициях на рис. 2.5 б:

>> T2=MoveTo(T,[7;8]);T3=MoveTo(T,[3;2]); show(T2,1,1,'y',1),show(T3,1,1,'c',1)

>> G2=1-exp(-K*dot(prod(Center(T2)),Si.*p)),G3=1-exp(-K*dot(prod(Center(T3)),Si.*p))

G2 = 0.9927 G3 =0.3789

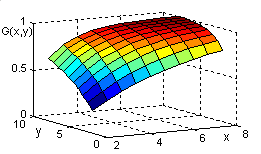
Рис. 2.6. Фрагмент КЗП

Размещая центр цели в узлах равномерной сетки (2 < x < 8, 2 < y < 8),  вычислим соответствующие этим положениям вероятности поражения цели и построим двумерный график зависимости G(x, y), характеризующий распределение вероятностей поражения цели в данной области. Первая команда строит равномерную сетку, вторая вычисляет в каждом узле среднее число попаданий в уязвимую площадь цели согласно формуле (2.17), последняя –  вычисляет и строит КЗП (рис. 2.6):

>> [I J]=meshgrid(linspace(-3,3,10),linspace(-3,3,10));

>> for i=1:100 m(i) =K*dot(prod(Center(Move(T,[I(i);J(i)]))),Si.*p); end

>> G=1-exp(-m); surf(I,J, reshape(G,size(I)))

Статистическое моделирование пуассоновского поля

Выполненные действия – лишь иллюстрация вычислений по формуле (2.16). На самом деле, плотность поля в процессе разлета далеко не всегда можно задать аналитическим законом. Искривление траекторий осколков зависит от их баллистических свойств и скорости (векторной). С учетом скорости носителя при воздушном подрыве начальные скорости разлета у всех осколков будут разными. Поэтому поле нужно рассматривать как совокупность дискретных элементов, а значит, его кинематику нельзя моделировать непрерывным преобразованием.

Статистическое моделирование рассматривает действие по цели каждого осколка в отдельности. Сформируем неоднородное поле так же, как и раньше, но плотность на прямоугольниках вычислим не по исходному закону, а по статистике попаданий, которая может учесть и результаты работы процедур, моделирующих движение осколков после формирования поля до расчетного момента. Создадим сразу N экземпляров поля, а затем методом PolyRect\Impact определим число попаданий в каждый элемент объекта T1:

>> m=0;n=70;N=500; x=sqrt(rand(N,n))*10; y=sqrt(rand(N,n))*10;

>> L=zeros(1,6);for j=1:N*n k=Impact(T1,[x(j);y(j)]); if k>0 L(k)=L(k)+1;end,end

В данном случае после формирования поля с заданным распределением плотности никаких изменений не вносится, поэтому при большом N плотность в центре каждого прямоугольника должна приближаться к среднему числу попаданий в него, отнесенному к площади данного прямоугольника:

>> L1=K*prod(Ci), Ls1=L./Si/N

L1 = 0.7000 0.4900 0.8575 0.9520 0.3675 0.6125

Ls1 = 0.7053 0.4840 0.8427 0.9356 0.3978 0.6200

Статистические оценки оказались очень близкими к точным значениям. Таким образом, для вычисления среднего числа попаданий вместо формулы (2.17) можно использовать результаты статистического моделирования процессов разлета осколков. Это избавляет от необходимости оперировать с плотностью поля, что очень важно, поскольку из статических испытаний известно распределение осколков относительно неподвижного снаряда, а плотность поля в целевой системе координат нельзя получить корректно простыми преобразованиями.

Контрольные вопросы и задачи

1. Чем отличается стохастически равномерное поле от равномерного распределения узловых точек в узлах равномерной сетки?

2. Случайное событие A_2, 4 – ровно m = 2 попадания в n = 2 независимых выстрелах. Выразите это событие через события A_k – попадание в k -м выстреле. Примените к полученному выражению теоремы сложения и умножения вероятностей. Обобщите результат для произвольных m, n.

3. Какова вероятность не менее K = 3 успехов в n = 10 испытаниях Бернулли с вероятностью успеха в каждом повторении p = 0,3?

4. Как вычислить вероятность не более K = 3 успехов в n = 100 испытаниях Бернулли с вероятностью успеха в каждом повторении p = 0,03?

5. Как получено выражение для вероятности данной комбинации числа событий в серии испытаний Бернулли с более, чем двумя возможными исходами?

6. Как получено выражение для вероятности данного числа успехов в серии независимых испытаний, когда вероятности успехов в разных испытаниях не одинаковы?

7. Объясните доказательство теоремы Пуассона.

8. На каком основании можно считать осколочное поле пуассоновским или простейшим пуассоновским?

9. Простейшее пуассоновское поле точек на плоскости имеет плотность 0,5. Какова вероятность попадания хотя бы одной точки в круг единичного радиуса?

10. Плотность нестационарного пуассоновского потока отказов линейно возрастает по закону (t) = a + b t. Какая вероятность того, что в интервале времени [t₁, t₂] не будет отказов?

11. Объясните вероятностный смысл координатного закона поражения.

12. Объясните вероятностный смысл функции уязвимости.

13. Чем объясняется возрастание КЗП от начала координат на рис. 2.8?

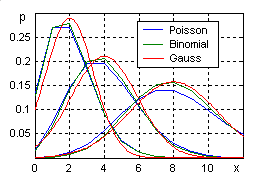
14. Выполнить количественную оценку степени приближения легко с помощью электронных формул. Построить многоугольники биномиального распределения при n = 40, p = 0,1 и Пуассона с параметром  = np = 4, а также график аппроксимирующей функции (2.9), повторить эту процедуру при n = 40, p = 0,2 и n = 40, p = 0,05.

Решение:

>> n=40; p=0.1; B=p_Binom(p,n); P=f_Poisson(n*p,n);

>> x=0:0.1:n; s=sqrt(n*p*(1-p)); G=f_Gauss((x-n*p)/s)/s;

>> plot(0:n, P, 0:n, B, x, G)

Рис. 2.1. Погрешности аппроксимации биномиальной формулы

Сравнение отклонений графиков нормального и пуассоновского приближений от результатов расчета по биномиальной формуле на рис. 2.1 показывает, в какой степени погрешности нормального приближения растут с приближением p к границам интервала [0, 1], а пуассоновского – при увеличении произведения np (положения максимума биномиального распределения) от 2 до 8. В варианте p = 0,05 и np = 2 точнее пуассоновское приближение, а p = 0,2 и np = 8 – нормальное. Это нужно учитывать, выбирая корректное приближение биномиальной формулы для решения практических задач.

ПРИЛОЖЕНИЕ к лекции 2

Листинг 2.1. Функция p_Binom

%Вычисляет вероятности возможного числа успехов (от 0 до n

% или заданного массивом m) в испытаниях Бернулли с параметрами n, p.

function out = p_Binom(p,n,m)

if nargin<3 m=0:n; end;

for i=1:length(m) out(i)=f_Binom(p,n,m(i)); end

%

function out = f_Binom(p,n,m)

out = CombiCount(n,m)*p^m*(1-p)^(n-m);

Листинг 2.2. Функция Гаусса f_Gauss

%Вычисляет функцию Гаусса

function f= f_Gauss(x)

f=exp(-x.^2/2)/sqrt(2*pi);

Листинг 2.3. Функция Trap

% Интегрирование методом трапеций

function out = Trap(f,x)

dx=diff(x); out=dot(f, [dx(1)/2 dx(1:end-1) dx(end)/2]);

Листинг 2.4. Функция Лапласа от скалярного аргумента f_Laplas

%Вычисляет функцию Лапласа

function out= f_Laplas(x)

t=linspace(0,x,50);

out=Trap(f_Gauss(t),t);

Листинг 2.5. Функция Лапласа от векторного аргумента f_LaplasV

%Вычисляет функцию Лапласа для всех элементов входного массива x

function F = f_LaplasV(x)

F=zeros(size(x)); n=prod(size(x));

for i=1:n F(i)=f_Laplas(x(i)); end

Листинг 2.6. Обратная функция Лапласа ArgLaplas

%Вычисляет аргумент функции Лапласа по ее значению

% По значению функции Лапласа вычисляет ее аргумент

%

function out = ArgLaplas(Ver)

for i=1:length(Ver)

out(i)=ArgLaplas_(Ver(i));

end

function X = ArgLaplas_(Ver)

x=linspace(0,4,200);dx=4/199;

I=find(cumsum(f_Gauss(x)*dx)-Ver>0);

X=x(I(2)); X=X+(Ver-f_Laplas(X))/f_Gauss(X);

Листинг 2.7. Формула Пуассона p_Poisson

% Вычисляет вероятности числа успехов по формуле Пуассона с параметром lambda;

% числа успехов задает вектор m,

% или 0:m, если m –отрицательный скаляр

%

function out= p_Poisson(lambda,m)

expa=exp(-lambda);

if length(m)>1

for i=1:length(m)

out(i)=a^m(i)*expa/factorial(m(i));

end

else

out(1)=expa;

for i=1:abs(m)

out(i+1)=out(i)*a/(i);

end

if m>0 out=out(end); end

end

Листинг 2.8. Обобщенная формула Бернулли RptTrial

% Вычисляет распределение вероятности числа успехов

% в n независимых испытаниях в одинаковых условиях (P - скаляр)

% или разных (в векторе P вероятности успеха в каждом испытании)

function [out, out2] = RptTrial(P,n)

if nargin>1 & length(P)==1 P(n)=P; end

if nargin==1 n=length(P);end

if length(n)==1 n=1:n; end

P=P(n);Q=1-P;

syms Z X;

X=strcat('[',strrep(char(expand(prod(P*Z+1-P))),'+',' '),']');

out2 = subs(X,Z,1); out = out2([end:-1:1]);

Листинг 2.9. Оценка вероятностей успеха в испытаниях Бернулли по частоте успехов.

% Вычисляет границы доверительного интервала вероятностей успеха

% в n испытаниях Бернулли по числу успехов pm при доверительной вероятности P

function p=I_Binom(pm,n,P)

p=[0,0];

if pm==0 p(2)=min_Binom(1-P,n,0);

elseif pm==n p(1)=1-min_Binom(1-P,n,1); p(2)=1;

else

x=pm/n;

t=ArgLaplas(P/2)^2/n;

A=1+t;

B=x+t/2;

C=x^2;

D=sqrt(B.^2-A*C);

p=[(B-D)/A,(B+D)/A];

end

%

function p=Min__Binom(P,n,x)

d=0.01; p=0.01; r=0;eps=0.0001;

for i=1:6

p=Fnd_Binom(P,n,x,p*0.9,-d);

if abs(r-p)<eps break; end

d=d/10;r=p;

end

Листинг 2.10. Функция оптимизирует параметры закона для аппроксимации зависимости дискретных реализаций F(x).

% Approx оптимизирует параметры выражения, аппроксимирующего функцию F(x)

% Law – аппроксимирующее выражение в виде строки символов

% x,F – массивы значений аргумента и функции

% P – исходное приближение (вектор) параметров аппроксимирующего выражения

function [Fun,Par]=Approx(Law,x,F,P)

Goal=inline(['sum((' Law '-F).^2)'],'P','x','F');

Par=fminsearch(Goal,P,optimset('MaxIter',200,'TolX',0.0001), x,F);

Fun=inline(Law,'x','P');