- •Лекция 10 Законы распределения функции двух случайных величин
- •Вероятностный смысл функции распределения двух св
- •Пример 1: распределение площади проекции вращающегося параллелепипеда
- •Объектный метод построения распределения площади проекции выпуклого многогранника
- •Применение объектного метода к произвольному многограннику Рис. 10.4.
- •Моделирование произвольного многогранника Рис. 10.5.
- •Пример 4: Перекрытие прямоугольных областей
- •Законы распределения мультипликативных функций двух св
- •Закон распределения произведения двух св
- •Закон распределения отношения двух св
- •Пример 5: распределение площади прямоугольника со случайными длинами сторон
- •Пример 6: распределение объема параллелепипеда
- •Пример 7: закон распределения отношения нормальных центрированных св
- •Пример 8: распределение фазы промаха
- •Законы распределения аддитивных функций двух св
- •Закон распределения суммы двух случайных величин
- •Законы распределения разности двух св
- •Композиция законов распределения
- •Композиция некоторых законов распределения
- •Композиция двух равномерных законов
- •Композиция нескольких равномерных законов
- •Получение реализаций нормального закона с помощью датчика случайных чисел
- •Композиция равномерного и нормального распределений
- •Композиция двух показательных распределений
- •Композиция нескольких показательных распределений
- •Закон Эрланга
- •Разность двух независимых показательных распределений
- •Композиция двух св, распределенных по закону Пуассона
- •Осколочное поле как суперпозиция пуассоновских полей
- •Композиция биномиальных распределений
- •Композиция нормальных распределений
- •Композиция двух независимых нормальных распределений
- •Композиция двух зависимых нормальных распределений
- •Композиция двух нормально распределенных случайных векторов
- •Композиция объектов Norm2
- •Распределение наименьшей и наибольшей из нескольких св
- •Распределение наибольшей из нескольких св
- •Распределение наименьшей из нескольких св
- •Наименьший промах при круговом нормальном рассеивании
- •Наиболее раннее событие из нескольких пуассоновских потоков
Лекция 10 Законы распределения функции двух случайных величин
Вероятностный смысл функции распределения двух св
Fy(y) G(y) = P(Y<y) = P((X1, X2) D(y) = {x1, x2 : (x1, x2) < y}).
Если система (X1, X2) имеет совместную плотность f(x1, x2), функцию распределения можно получить интегрированием по области D(y):
![]()
Общий принцип получения законов распределения функций СВ сводится к целесообразному представлению области интегрирования.
Пример 1: распределение площади проекции вращающегося параллелепипеда
|
|
|
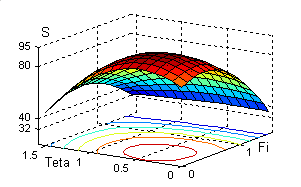
Рис. 10.1. Поверхность S(, ) и ее линии уровня |
>> a=10;b=8;c=4;A=c*b;B=a*c;C=a*b;
>> [Fi, Teta]= meshgrid(0:0.1:pi/2,0:0.1:pi/2);
>> S=A*sin(Fi)+(B*sin(Teta)+C*cos(Teta)).*cos(Fi); surfc(Fi, Teta, S)
|
|
|
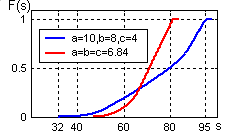
Рис. 10.2. Функция распределения F(s) |
>> [x,F, f]=Para3_Distrib(a,b,c);plot(x,F), hold on,m = Trap(x.*f,x),d=Trap(f.*(x-m).^2,x)
m = 75.9503 d = 223.5303
Алгоритмическое построение функции распределения позволяет исследовать вероятностную модель готовых поражающих элементов в форме параллелепипеда. Построим для сравнения функцию распределения проекции равновеликого куба:
>> h=(a*b*c)^(1/3);
[x,F,f]=Para3_Distrib(h,h,h); plot(x,F),m=Trap(x.*f,x),M=6*h^2/4, d = Trap(f.*(x-m).^2,x)
m = 70.2376 M = 70.1784 d = 50.8886
Первый начальный момент m практически совпал с точным значением M средней площади проекции согласно лемме Коши. Графики на рис. 10.2 показывают меньший разброс площади проекции компактного тела, что подтверждает и вычисленная дисперсия d. Оптимизация линейных размеров поражающего элемента может существенно повлиять на эффективность действия. Еще большее влияние может оказать изменение межреберных углов, но такой анализ не предусмотрен в программе Para3_Distrib, расчетные процедуры в которой построены для параллелепипедов.
|
|
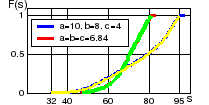
|
Рис. 10.3. Сравнение точных и статистических функций распределения F(s) |