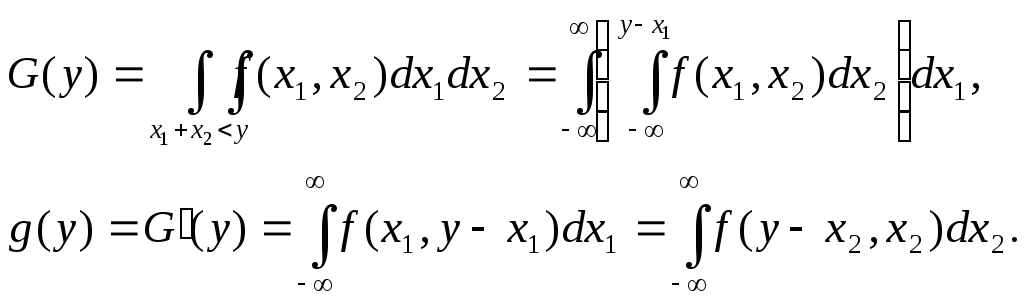- •Лекция 10 Законы распределения функции двух случайных величин
- •Вероятностный смысл функции распределения двух св
- •Пример 1: распределение площади проекции вращающегося параллелепипеда
- •Объектный метод построения распределения площади проекции выпуклого многогранника
- •Применение объектного метода к произвольному многограннику Рис. 10.4.
- •Моделирование произвольного многогранника Рис. 10.5.
- •Пример 4: Перекрытие прямоугольных областей
- •Законы распределения мультипликативных функций двух св
- •Закон распределения произведения двух св
- •Закон распределения отношения двух св
- •Пример 5: распределение площади прямоугольника со случайными длинами сторон
- •Пример 6: распределение объема параллелепипеда
- •Пример 7: закон распределения отношения нормальных центрированных св
- •Пример 8: распределение фазы промаха
- •Законы распределения аддитивных функций двух св
- •Закон распределения суммы двух случайных величин
- •Законы распределения разности двух св
- •Композиция законов распределения
- •Композиция некоторых законов распределения
- •Композиция двух равномерных законов
- •Композиция нескольких равномерных законов
- •Получение реализаций нормального закона с помощью датчика случайных чисел
- •Композиция равномерного и нормального распределений
- •Композиция двух показательных распределений
- •Композиция нескольких показательных распределений
- •Закон Эрланга
- •Разность двух независимых показательных распределений
- •Композиция двух св, распределенных по закону Пуассона
- •Осколочное поле как суперпозиция пуассоновских полей
- •Композиция биномиальных распределений
- •Композиция нормальных распределений
- •Композиция двух независимых нормальных распределений
- •Композиция двух зависимых нормальных распределений
- •Композиция двух нормально распределенных случайных векторов
- •Композиция объектов Norm2
- •Распределение наименьшей и наибольшей из нескольких св
- •Распределение наибольшей из нескольких св
- •Распределение наименьшей из нескольких св
- •Наименьший промах при круговом нормальном рассеивании
- •Наиболее раннее событие из нескольких пуассоновских потоков
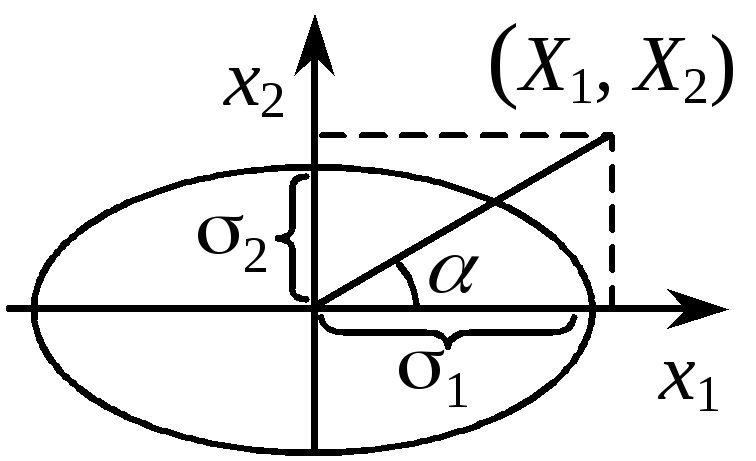
Пример 7: закон распределения отношения нормальных центрированных св
|
|
(10.4) |
В самом
деле, если f(u1, u2) = (u12 + u22),
то f(u1, y u1) = (![]() ).
Вид функции не
имеет значения, поскольку после замены
переменной
).
Вид функции не
имеет значения, поскольку после замены
переменной
![]() получим (подынтегральная функция
четная):
получим (подынтегральная функция
четная):
![]()
где постоянная C определяется из условия
![]() .
.
Таким
образом, СВ Y =![]() распределена по закону Коши, а так как
Z =
распределена по закону Коши, а так как
Z = ![]() ,
(z) =
,
(z) = ![]() ,
(z) =
,
(z) = ![]() ,
отношение координат Z
подчиняется закону
,
отношение координат Z
подчиняется закону
![]()
Пример 8: распределение фазы промаха
|
|
|
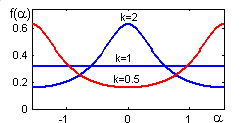
Рис. 10.11. Фаза промаха |
|
|
(10.5) |
Построим графики плотности распределения фазы промаха при круговом рассеивании (k = 1), а также при 1> 2 (k = 2) и 1< 2 (k = 0,5):
>> x=[-1:0.01:1]*pi/2;k=1; y=k./(cos(x).^2+k^2*sin(x).^2)/pi; hold off, plot(x,y)
>> k=2; y=k./(cos(x).^2+k^2*sin(x).^2)/pi; hold on, plot(x,y)
>> k=0.5; y=k./(cos(x).^2+k^2*sin(x).^2)/pi; hold on, plot(x,y,'k')
|
|
|
Рис. 10.12. Плотность распределения фазы промаха |
Законы распределения аддитивных функций двух св
Закон распределения суммы двух случайных величин
|
а б |
|
Рис. 10.13. Область интегрирования для суммы СВ |
|
|
(10.6) (10.7) |
Если
интервалы возможных значений слагаемых
ограничены, соответственно ограничена
и область интегрирования Dy
(рис. 10.13 б). В частности, область
интегрирования положительных слагаемых
представляет собой треугольник
![]() = {x1,
x2 : x2 < y – x1,
x1>0, x2 >0},
а в формуле (10.7) бесконечные пределы
интегрирования следует заменить на
[0, y]:
= {x1,
x2 : x2 < y – x1,
x1>0, x2 >0},
а в формуле (10.7) бесконечные пределы
интегрирования следует заменить на
[0, y]:
|
|
(10.8) |
Законы распределения разности двух св
|
|
(10.9) |
Композиция законов распределения
|
|
(10.10) |
Некоторые законы распределения обладают свойством устойчивости по отношению к композиции, т.е. композиция двух и более СВ с одним из таких законов распределения, подчиняется тому же закону.