Композиция двух св, распределенных по закону Пуассона

Если X₁, X₂ независимые СВ, распределенные по закону Пуассона с параметрами a₁, a₂, возможные значения суммы Y = X₁ + X₂ – все целые числа (с нулем), а вероятности p_k = P(Y = k), можно выразить через параметры слагаемых СВ дискретным аналогом формулы (10.10):

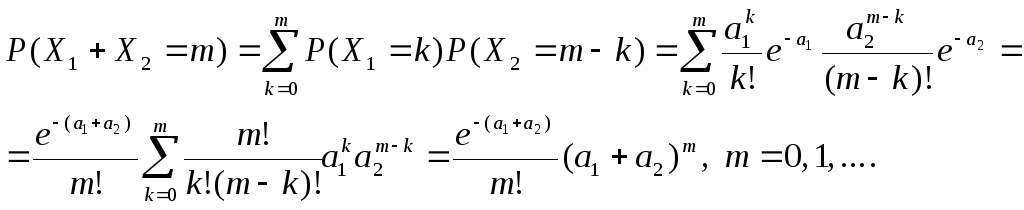
Закон Пуассона устойчив к композиции. Это значит, что совмещение нескольких простейших пуассоновских полей (суперпозиция полей) образует простейшее пуассоновское поле.

Осколочное поле как суперпозиция пуассоновских полей

Осколочное поле представляет собой пространственное совмещение полей, создаваемых разными фракциями. Эти поля могут быть неоднородными на всей проекции цели, но в пределах одного i-о УА плотность поля от k-й фракции можно считать зависящей только от координат центра разрыва относительно центра данного УА _k(x_i, y_i, z_i). Попавший в i-й УА осколок k-й фракции выводит его из строя с вероятностью p_ki, зависящей для данного УА от массы q_k и скорости встречи v. Участок осколочного поля на проекции УА можно представить как суперпозицию простейших пуассоновских полей с плотностями «поражающих» осколков _k(x_i, y_i, z_i)p_ki(q_k, v), а вероятность поражения – как вероятность наступления хотя бы одного события в распределении Пуассона с параметром

.

(10.13)

Композиция биномиальных распределений

Выборочный контроль качества изготавливаемых изделий проводится по схеме Бернулли: из партии наугад выбирают контрольную группу (n штук), в ней выявляют дефектные изделия, их количество сравнивают с критическим (приемочным) числом. При известной частоте дефектных изделий в партии (вероятности обнаружения дефекта p) число дефектных изделий в контрольной выборке X подчиняется биномиальному закону с параметрами n, p. В случае небольшого превышения критического числа обнаруженных дефектов берут вторую выборку (метод двукратной выборки). Если общее число дефектных изделий не превышает установленное второе критическое число, партия принимается. Речь идет о композиции двух СВ X₁, X₂, распределенных по биномиальному закону с параметрами, соответственно, (n₁, p) и (n₂, p). Число успехов в испытаниях Бернулли равно сумме индикаторов успеха в i-м опыте:

, ,

так как P(X = 1) = p в обоих опытах. Общее число успехов

Y = X₁ + X₂ =

подчиняется биномиальному закону с параметрами n = n₁ + n₂ и p.

Таким образом, устойчивость относительно сложения – не только асимптотическое свойство закона Пуассона, аппроксимирующего биномиальное распределение, но фундаментальное свойство распределений, вытекающих из условий испытания Бернулли. Значит, оно должно быть присуще и другому «родственнику» биномиального закона (согласно локальной теореме Лапласа) – нормальному закону.

Композиция нормальных распределений

Композиция двух независимых нормальных распределений

Предположим вначале, что XN(m₁, ₁), Y  N(m₂, ₂) независимы. Их сумма Z = X + Y имеет плотность распределения согласно (10.25)

.

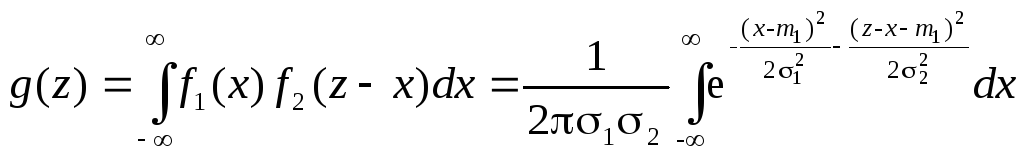Показатель степени можно представить в виде квадратного трехчлена (x) = – Ax² + 2Bx – C, в котором A > 0 не зависит от z, коэффициент B содержит z в первой степени, в коэффициент C – во второй. Из интегрального исчисления известно, что

.

Функция вида со свойствами плотности распределения может быть только функцией Гаусса (4.13). Это значит, что композиция двух нормальных распределений также подчиняется нормальному закону. Параметры этого распределения можно определить из структуры коэффициентов a и t, но их легче найти по теореме о числовых характеристиках:

M_z = M[X₁] + M[X₂] = m₁ + m₂,

.