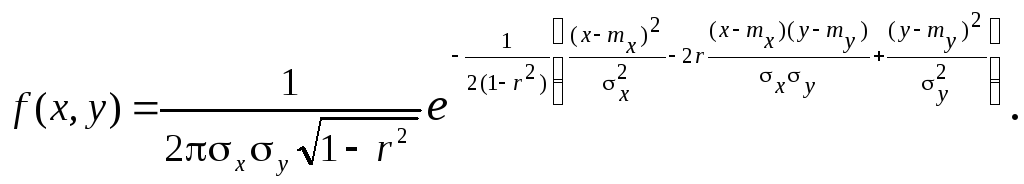_Лекция

₇

Двумерное нормальное распределение

Пример системы двух нормально распределенных СВ – случайные отклонения точки падения снаряда на плоскости расположения целей. Для вычисления вероятности попадания в цель, осреднения условных вероятностей поражения по области рассеивания нужна функция плотности распределения двумерного нормального закона.

Определение многомерного нормального закона

Распределение двух и более СВ называется нормальным, если каждая СВ системы подчиняется нормальному закону. Из этого определения следует, что f(x, y) – плотность двумерного нормального закона, если ее интегрирование по всем возможным значениям одной СВ дает нормальный закон распределения другой:

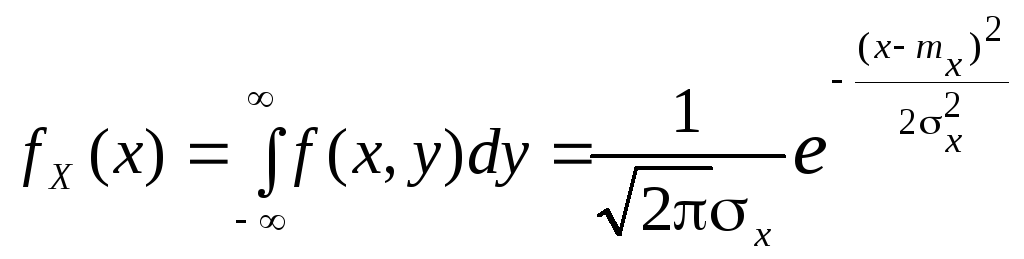
и такой же закон f_Y(y) с параметрами m_y, _y. 

Совместная плотность независимых нормально распределенных СВ

Если X, Y независимы, f(x, y) можно получить из частных распределений:

.

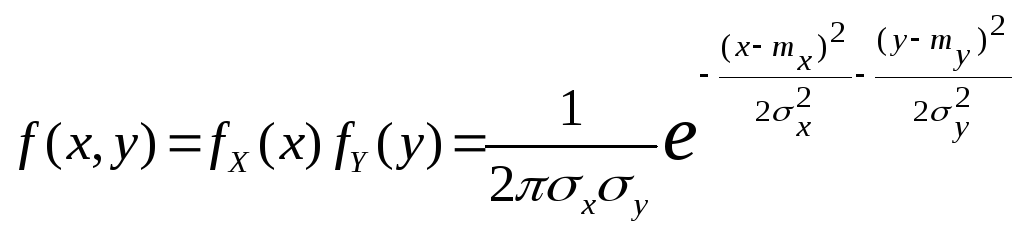(7.1)

Каноническое двумерное нормальное распределение

Наиболее простой вид двумерный нормальный закон принимает при отсутствии систематических ошибок m_x = m_y = 0. Система (₁, ₂) независимых, центрированных СВ ₁ N(0, ₁) и ₂  N(0, ₂) имеет плотность нормального распределения в канонической форме:

.

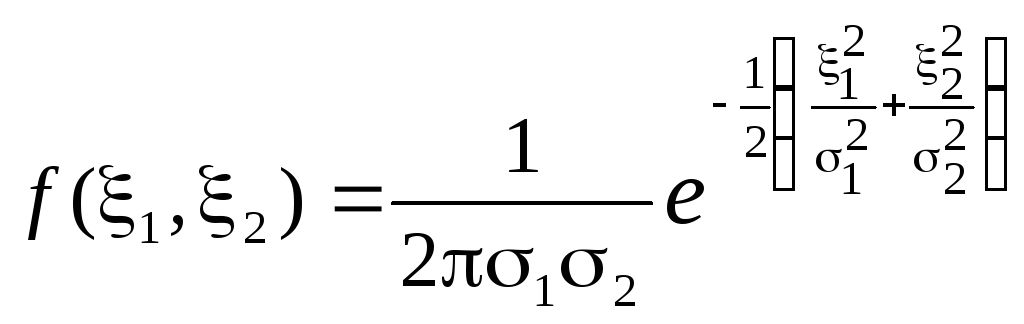(7.2)

Эллипс рассеивания

Эллипс, на котором показатель степени в (7.2), а значит и плотность распределения, имеют постоянное значение,

Bk =

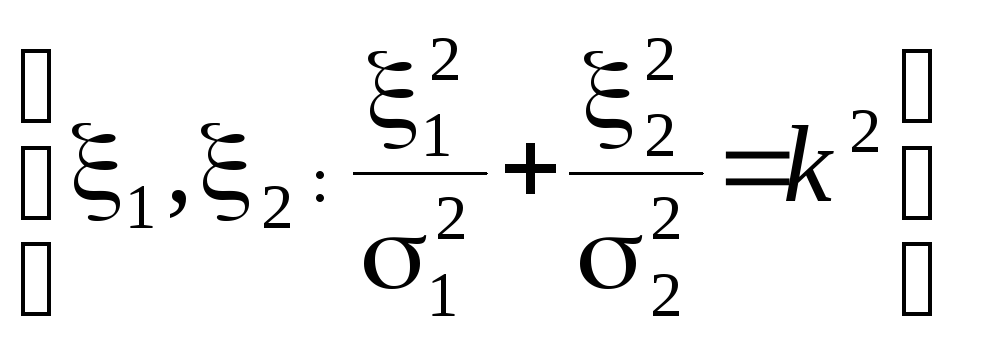
(7.3)

называется эллипсом равной плотности, ограниченная им область – эллипсом рассеивания, центр эллипса – центром рассеивания. Плотности f₁(₁) и f₂(₂) различны в разных точках эллипса с полуосями k₁, k₂ (рис. 7.1), но произведение f₁(₁) f₂(₂) = f(₁, ₂) постоянно при данном значении k.

Ортогональное преобразование главных осей

Компоненты того же случайного вектора в произвольной системе координат x₁Ox₂, в которой направления осей не совпадают с главными осями рассеивания уже не будут независимы (хотя бы потому, что линии регрессии не параллельны осям координат). Значение функции f(x, y) совпадает с плотностью канонического нормального распределения в той же точке. Закон распределения f(x, y) можно получить преобразованием канонического закона при повороте главных осей на некоторый угол  до совпадения с x₁Ox₂ :

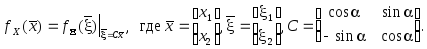
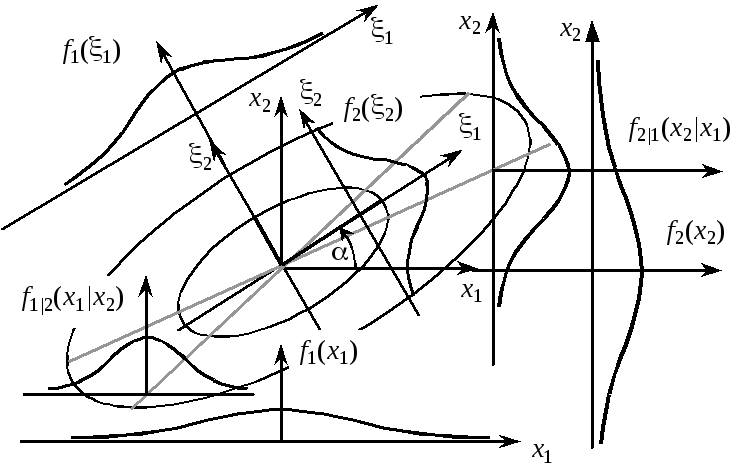
Рис. 7.1. Двумерное нормальное распределение в главной (₁, ₂)  и произвольной (x₁, x₂) системах координат

В главной системе координат эллипсы равной плотности представляются квадратичными формами с диагональной матрицей D ^– 1, обратной к матрице, состоящей из главных дисперсий:

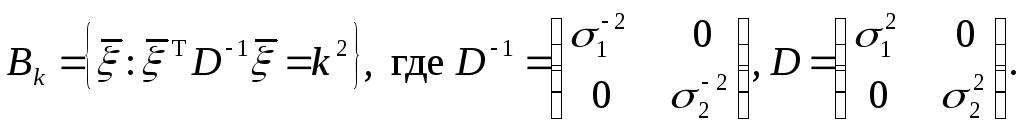
Если векторы и связаны преобразованием матрица D получена преобразованием D = CKC^T матрицы K, которая должна быть матрицей корреляционных моментов, чтобы выполнялось D_ii = _i², i = 1, 2: 

.

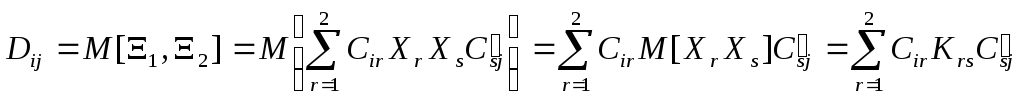Эллипс B_k  в произвольной системе x₁Ox₂ образуется симметричной матрицей K ^– 1 = C^TD ^–1C, обратной к корреляционной матрице K:

так как из того, что D = CKC^T, D ^–1 = (C^T)^–1K ^–1C ^–1 следует C^TD ^–1C = K ^–1.

Многомерный нормальный закон в канонической векторной форме

Квадратичную форму в (7.2) можно заменить матричным выражением, а произведение ₁₂ выразить через определитель корреляционной матрицы:

.

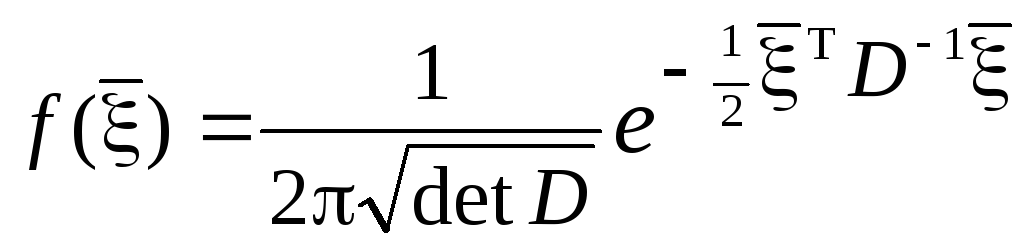Канонический двумерный нормальный закон в векторной форме легко обобщить на n-мерный нормально распределенный случайный вектор:

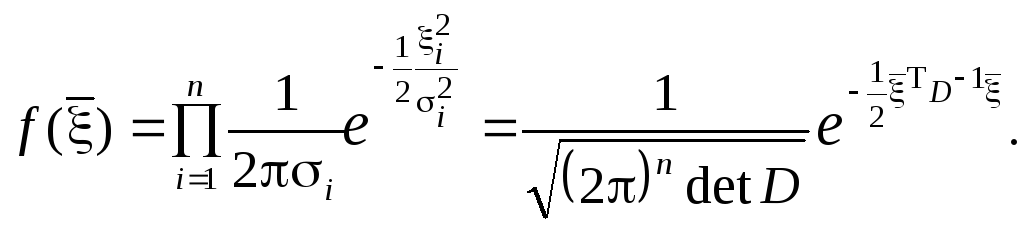
(7.4)

Нормальный закон многомерного вектора в общем виде

В произвольной системе координат, в которой корреляционная матрица K не обязательно диагональная, а центр рассеивания находится в точке , плотность распределения имеет вид нормального закона в общей форме:

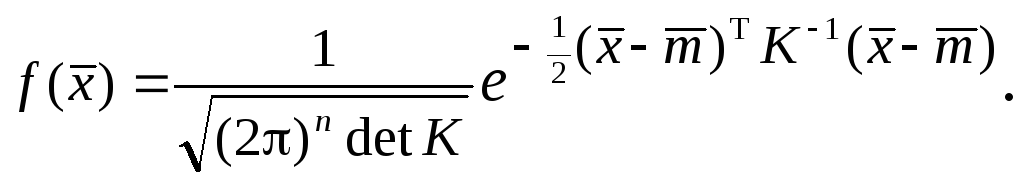
(7.5)

Нормальное распределение на плоскости в координатной форме

Нормальное распределение системы (X, Y) в общем случае задается МО m_x = M[X], m_y = M[Y], а также дисперсиями D_x, D_y и корреляционным моментом K_xy или СКО _x, _y и коэффициентом корреляции r, определяющими корреляционную матрицу

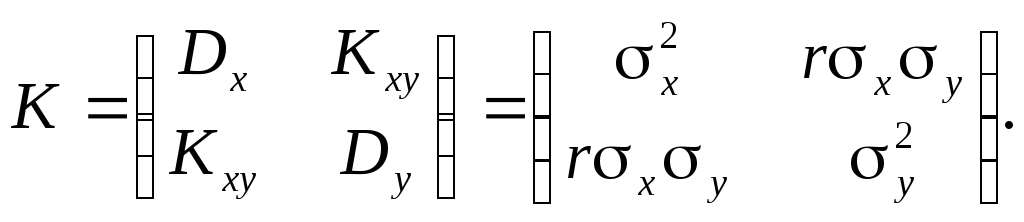
(7.6)

Выразив определитель detK и обратную матрицу K^–1 через параметры рассеивания

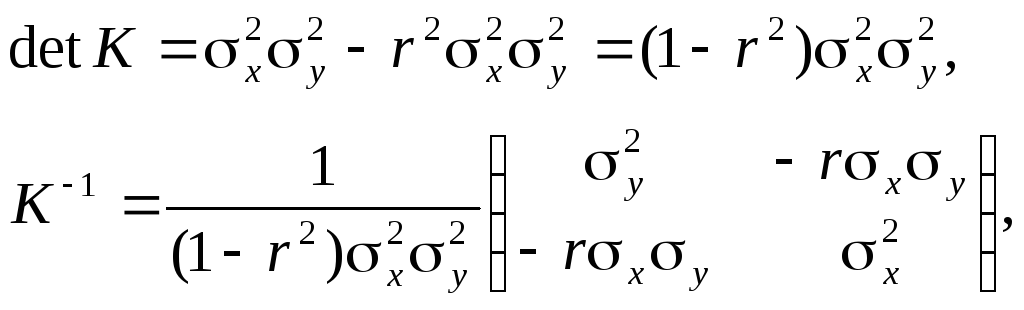
и подставив их в (7.5) при n = 2, получим плотность двумерного нормального распределения, заданного параметрами m_x, m_y, _x, _y, r:

(7.7)

В частности, при r = 0 формула (7.7) превращается в нормальный закон двух независимых СВ, а при m_x = m_y= 0 – в каноническую форму двумерного нормального распределения.

Проекции нормального распределения

Интегрирование совместной плотности (7.7) по одной из переменных дает нормальное распределение другой СВ:

.

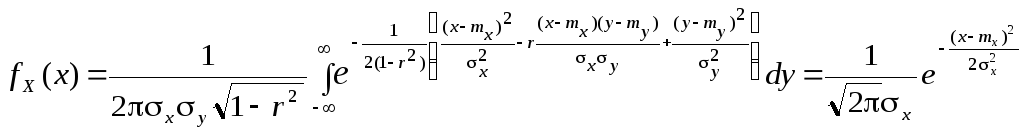Действительно, после стандартной замены переменных

, , dy = _yd

интегрирование по частям

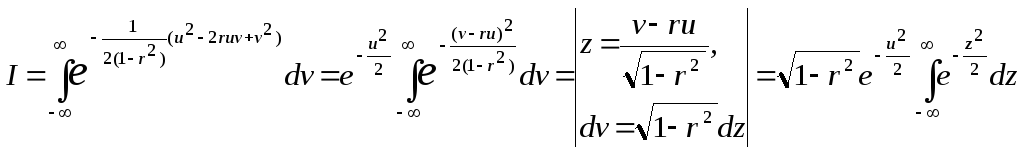
с учетом интеграла Пуассона дает окончательный результат:

.

Условные распределения нормального закона

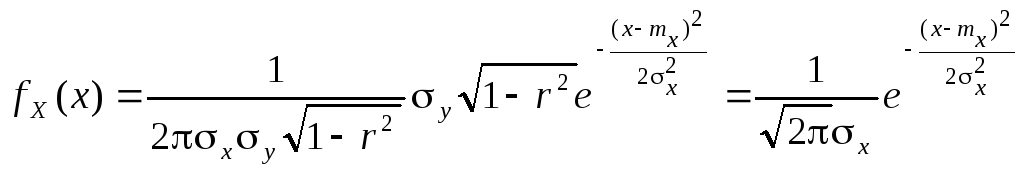Применяя теорему умножения плотностей, получим условные распределения нормального закона:

.

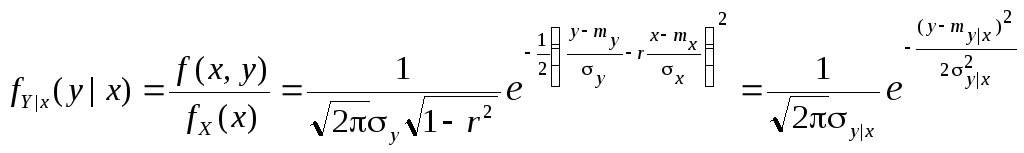Условная плотность подчиняется нормальному закону с параметрами m_y|x, _y|x и свойствами нормальной регрессии (6.26) – (6.29): линейная регрессия с постоянной условной дисперсией, некоррелированность означает независимость системы.

Если СВ системы однородны (например, координаты случайной точки на плоскости), их можно сделать независимыми надлежащим поворотом системы координат.