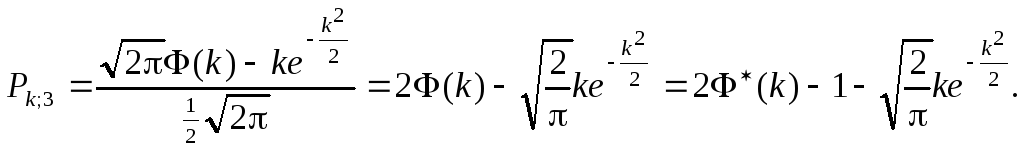- •Ортогональное преобразование главных осей
- •Многомерный нормальный закон в канонической векторной форме
- •Нормальный закон многомерного вектора в общем виде
- •Нормальное распределение на плоскости в координатной форме
- •Проекции нормального распределения
- •Условные распределения нормального закона
- •Переход к главной системе координат
- •Круговое рассеивание
- •Параметры рассеивания в главной системе координат
- •Вероятность попадания в эллипс рассеивания
- •Вероятность попадания в эллипс рассеивания
- •Обобщение на n -мерные эллипсоиды рассеивания
- •Вероятность попадания в 3-мерный эллипсоид рассеивания
- •Случайная величина «хи-квадрат»
- •Закон распределение n-мерного промаха
- •Числовые характеристики n-мерного промаха
- •Закон Рэлея и его числовые характеристики
- •Срединный промах в 1.75 раз больше срединного отклонения
- •Вычисление интегральных показателей, зависящих от распределения промахов
- •Вероятность попадания в заданную область
- •Вероятность попадания в эллипс рассеивания
- •Вероятность попадания в эллипс рассеивания в масштабе срединных отклонений
- •Вероятность попадания в круг
- •Вероятность попадания в эллипсоид
- •Вычисление вероятности попадания в цилиндр
- •Вероятность попадания в прямоугольник
- •Вероятность попадания в произвольную область
- •Требования к аппарату вычисления вероятностей папаания
- •Класс двумерных нормально распределенных случайных векторов
- •Структура и методы класса Norm_2
- •Пример 1. Вычисление вероятностей попадания в группу объектов
- •Пример 2. Статистическое моделирование в классе Norm_2
- •Пример 3. Оптимизация параметров распределения
- •Пример 4. Оптимизация ско рассеивания
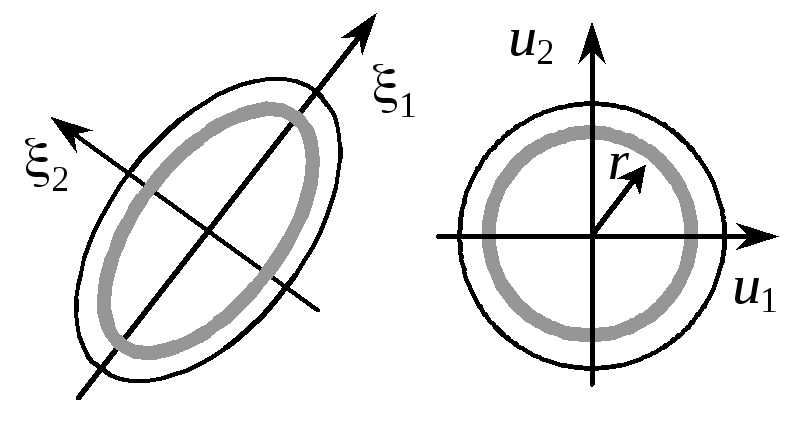
Переход к главной системе координат
![]()
![]()
откуда следует
|
|
(7.8) |
Круговое рассеивание
Параметры рассеивания в главной системе координат
-
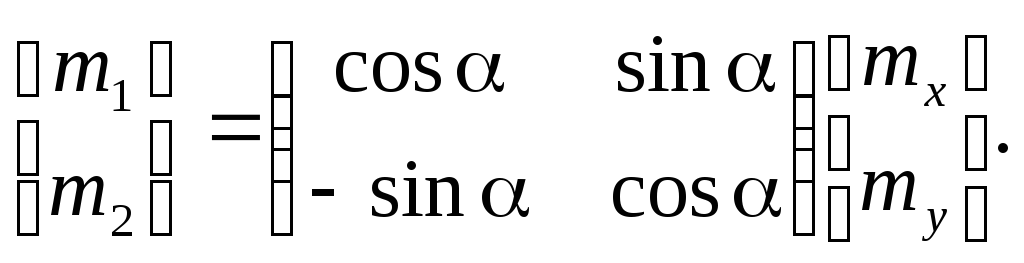
(7.9)
Дисперсии можно получить как диагональные элементы матрицы D = СKCT :
-
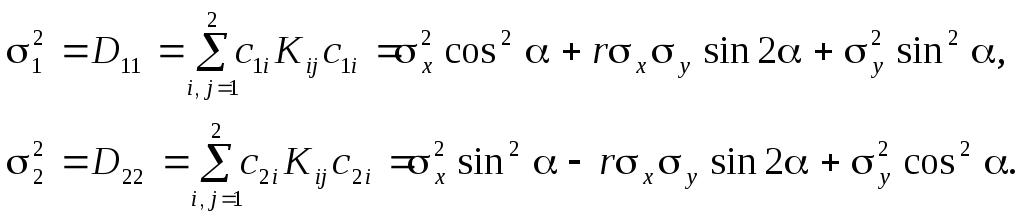
(7.10)
(7.11)
По этим формулам вычисляют дисперсии после поворота системы координат на угол , и, в частности, главные СКО 1, 2, если угол соответствует отношению (7.8). В главных осях рассеивания лучше проявляются инвариантные свойства распределения и проще вычислять вероятности попадания случайной точки в заданную область.
Вероятность попадания в эллипс рассеивания
Вероятность попадания в эллипс рассеивания
|
|
|
Рис. 7.2. Переход к интегрированию по кольцевым слоям |
|
|
(7.12) |
Обобщение на n -мерные эллипсоиды рассеивания
![]() ,
i = 1, …, n
эллипсоид превращается в n-мерную
сферу, вероятность попадания в слой (r,
r + dr)
теперь пропорциональна
,
i = 1, …, n
эллипсоид превращается в n-мерную
сферу, вероятность попадания в слой (r,
r + dr)
теперь пропорциональна
![]() ,
а суммарная вероятность выражается
интегралом
,
а суммарная вероятность выражается
интегралом
|
|
(7.13) |
где С – постоянная, которую можно найти из условия, что вероятность попадания в бесконечно большой эллипсоид равна единице (P; n = 1).
При n = 2 Pk; 2 совпадает с pk, определяемым формулой (7.12).
Вероятность попадания в 3-мерный эллипсоид рассеивания
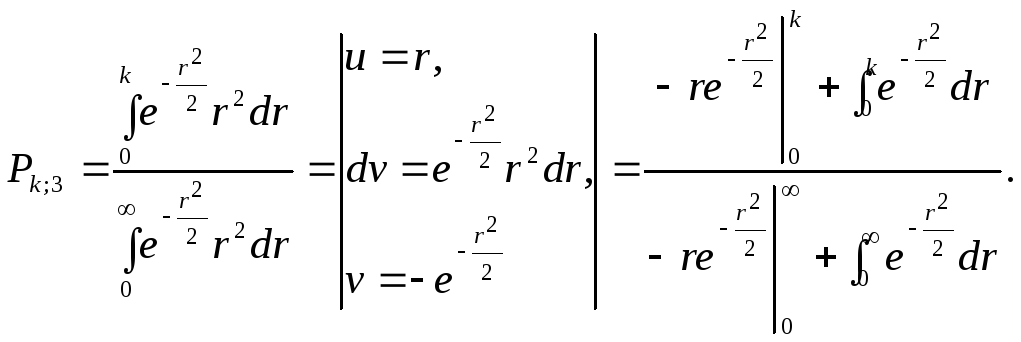
Определенный интеграл в числителе можно выразить через функцию Лапласа или стандартную функцию распределения:
|
|
(7.14) |

 .
.
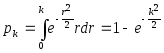 .
.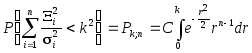 .
.