Вычисление интегральных показателей, зависящих от распределения промахов

На основании закона распределения n-мерного промаха получены выражения для ЧХ промаха, но этого недостаточно, если важен не сам промах, а некоторое действие на промахе. Например, вероятность поражения цели как функцию промаха – условный закон поражения U(r) – нужно усреднить по всем возможным промахам для получения полной вероятности поражения. Вычисления по интегральной формуле полной вероятности (функция Trap) оперируют с поэлементным произведением значений условного закона и плотности распределения на расчетной сетке. Для вычисления f(r_i) можно воспользоваться функцией Rayl, реализующей формулу (7.21), или аналогичной реализацией закона Максвелла в пространственном случае. Универсальная функция Chi2pdf(k,n) из библиотеки MATLAB вычисляет плотность распределения СВ «хи-квад­рат» с n степенями свободы f_Y(y, n), где y можно интерпретировать как квадрат промаха. Плотность распределения промахов r =  в n-мерном пространстве при круговом рассеивании с параметром  можно получить через функцию f_Y(y, n) следующим образом (Лекция 10):

.

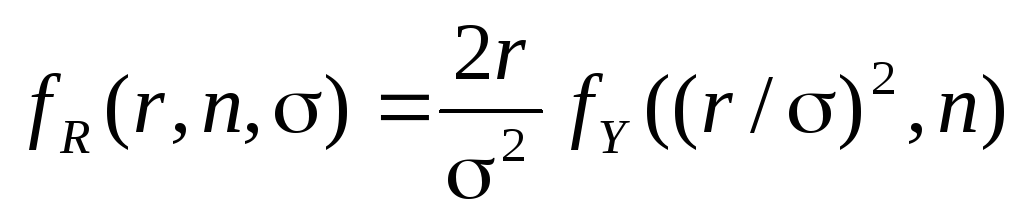(7.22)

Специально созданная файл-функция f_Ellipsoid(k,n,s) реализует вычисления по формуле (7.16), принимая вектор значений промаха k, число измерений n и СКО кругового рассеивания s (Листинг 7.2). Используем ее для построения нескольких графиков плотности распределения промахов при круговом рассеивании с параметром  = 1 в пространствах 2, 3, 4 и 10 измерений (рис. 7.5):

>>figure(3), hold on,s=1;k=0:0.1:10; for n=[2 3 4 10] P=f_Ellipsoid(k,n,s); plot(k,P),end

Последний график (n =10) построим также с помощью Chi2pdf, задав ее аргументы согласно формуле (7.24), и выведем этот график точками:

>> P=Chi2pdf((k/s).^2,10).*k*2/s^2; plot(k,P,'.')

Рис. 7.5. Плотность распределения n-мер-ного отклонения при шаровм рассеивании

Мы убедились, что вычисления по обеим функциям дают одинаковый результат, но нужно учитывать отличную от промаха интерпретацию аргумента в функции Chi2pdf. Наименьшую моду Mo =  имеет закон Рэлея, далее следует закон Максвелла, а с увеличением числа измерений (числа слагаемых «хи квад­рат») закон распределения становится почти симметричным. Есть основания полагать, что он приближается к нормальному закону. Чтобы убедиться в этом, построим график нормального закона с параметрами m_r, σ_r при n =10, вычислив эти параметры по формулам (7.17), (7.18):

>> n=10;m10=s*sqrt(2)*gamma((n+1)/2)/gamma(n/2);s10=sqrt(n*s^2-m10^2);

>> X=Norm_1(m10,s10); plot(k,f(X,k),'r--')

Так же построенный нормальный закон с параметрами, вычисленными при n =10 имеет заметное отличие от истинного. Вычислим Мо и дисперсию промаха на плоскости по интегральным формулам с использованием функции f_Ellipsoid и по формулам (7.22), (7.23):

>> s=1.5;k=0:0.05:10; P=f_Ellipsoid(k,2,s); Mr=Trap(k.*P,k),mr=sqrt(pi/2)*s

Mr = 1.8800 mr = 1.8800

>> Dr=Trap((k-mr).^2.*P,k),dr=s^2*(2-pi/2)

Dr = 0.9654 dr = 0.9657

Вероятность попадания в заданную область

Вероятность попадания в заданную область при нормальном рассеивании можно определить аналитически или с помощью таблиц лишь в отдельных случаях, в которых область задана эллипсами (эллипсоидами) рассеивания или интервалами отдельных СВ в независимой системе (параллелепипеды в главных осях рассеивания).