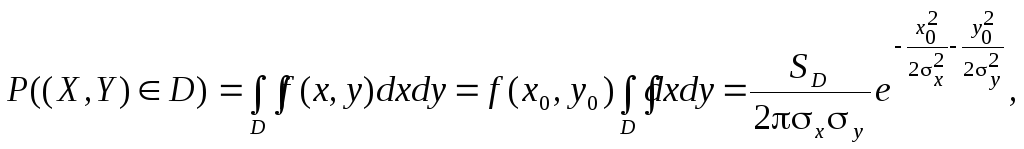- •Ортогональное преобразование главных осей
- •Многомерный нормальный закон в канонической векторной форме
- •Нормальный закон многомерного вектора в общем виде
- •Нормальное распределение на плоскости в координатной форме
- •Проекции нормального распределения
- •Условные распределения нормального закона
- •Переход к главной системе координат
- •Круговое рассеивание
- •Параметры рассеивания в главной системе координат
- •Вероятность попадания в эллипс рассеивания
- •Вероятность попадания в эллипс рассеивания
- •Обобщение на n -мерные эллипсоиды рассеивания
- •Вероятность попадания в 3-мерный эллипсоид рассеивания
- •Случайная величина «хи-квадрат»
- •Закон распределение n-мерного промаха
- •Числовые характеристики n-мерного промаха
- •Закон Рэлея и его числовые характеристики
- •Срединный промах в 1.75 раз больше срединного отклонения
- •Вычисление интегральных показателей, зависящих от распределения промахов
- •Вероятность попадания в заданную область
- •Вероятность попадания в эллипс рассеивания
- •Вероятность попадания в эллипс рассеивания в масштабе срединных отклонений
- •Вероятность попадания в круг
- •Вероятность попадания в эллипсоид
- •Вычисление вероятности попадания в цилиндр
- •Вероятность попадания в прямоугольник
- •Вероятность попадания в произвольную область
- •Требования к аппарату вычисления вероятностей папаания
- •Класс двумерных нормально распределенных случайных векторов
- •Структура и методы класса Norm_2
- •Пример 1. Вычисление вероятностей попадания в группу объектов
- •Пример 2. Статистическое моделирование в классе Norm_2
- •Пример 3. Оптимизация параметров распределения
- •Пример 4. Оптимизация ско рассеивания
Вероятность попадания в эллипсоид
-
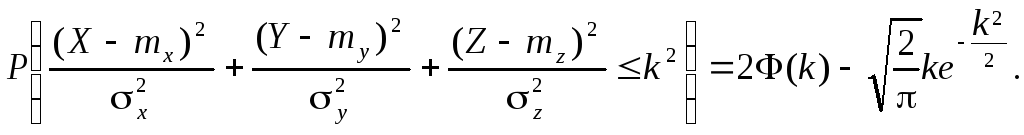
(7.27)
Тот же результат можно получить с помощью электронной формулы p_Ellipsoid(k,3). Вероятность попадания в шар радиуса r при x= y= z= и отсутствии систематических ошибок mx= my= mz = 0 можно вычислять по этой же формуле с подстановкой k = r / :
-
P(R<r) = FR(r) =
 .
.(7.28)
Плотность распределения промахов при шаровом рассеивании подчиняется закону Максвелла:
fR(r) = FR(r) =
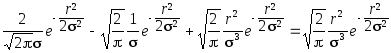 .
.
Для вычислений удобно воспользоваться электронной формулой fR(r) = Ellipsoid(r/sigma ,3).
Вычисление вероятности попадания в цилиндр

Вероятность попадания в прямоугольник
-
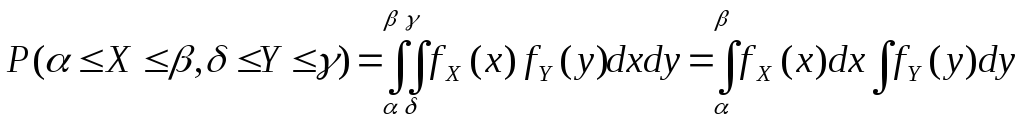 .
.(7.29)
С помощью таблиц функции Лапласа или стандартного нормального распределения * вычисления по формуле (7.29) можно выполнить одинаковой подстановкой аргументов:
-
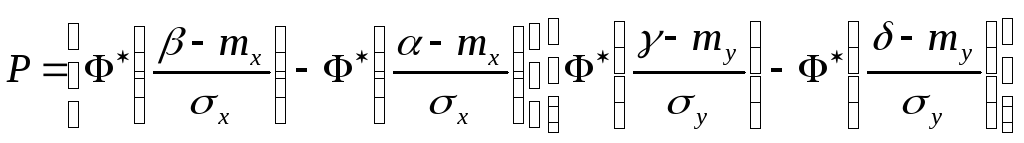 .
.(7.30)
Если характеристики
рассеивания заданы вероятными
отклонениями, удобно использовать
приведенную функцию Лапласа
![]() :
:
-
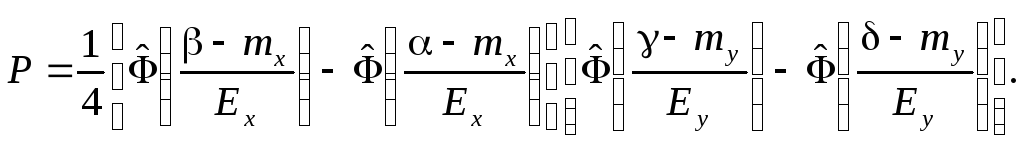
(7.31)
Вероятность попадания в n-мерный параллелепипед в главных осях рассеивания получается перемножением вероятностей попадания в проекции:
-
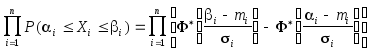 .
.(7.32)
В случае произвольной ориентации параллелепипеда придется прибегать к численному интегрированию. Это удобнее делать в той системе координат, в которой стороны прямоугольника параллельны осям:
![]() .
.
Вероятность попадания в произвольную область
|
|
(7.33) |
где x0, y0 – координаты центра области D в системе главных осей рассеивания. Если центр области совпадает с центром рассеивания (x0 = 0, y0 = 0),
-
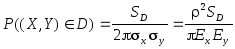 .
.(7.34)
Требования к аппарату вычисления вероятностей папаания