28. Оценка погрешности восстановления сигнала по дискретным отсчетам.

Представим полезный сигнал в виде х(t) = Вf(t),

где f (t) — известная функция времени; В — параметр сигнала.

Задача состоит в том, чтобы по принятой выборке Y определить, каково значение параметра В в полезном сигнале X.

В отличие от случаев обнаружения и различия сигналов здесь имеет место бесконечное множество возможных значений параметра В и, соответственно, бесконечное множество гипотез. Методы, рассматриваемые в случае двухальтернативных и многоальтерна­тивных ситуаций, применимы и для задачи восстановления сигнала.

Произведем оценку параметра В методом максимума правдоподобия. Если отсчет принятого сигнала производится в дискретные моменты времени, то функция правдоподобия для параметра В будет оавна

(8.56)

Задача состоит в том, чтобы найти такое значение параметра В для которого функция правдоподобия максимальна. Максимуму функции правдоподобия соответствует минимальное значение показателя степени в выражении (8.56)

Из условия минимума имеем

откуда получаем оценочное значение параметра

Осуществив переход к непрерывному примеру, получим

где — удельная энергия сигнала (энергия сигнала при амплитуде В = 1).

Для оценки точности восстановления сигнала используем критерий среднеквадратического отклонения. С этой целью в (8.58) принимаемый сигнал выразим в виде суммы у (t) = Bf (t) + ξ (t). Тогда

Погрешность восстановления

Дисперсия погрешности

Среднее от произведения ξ (t₁)ξ (t₂) представляет корреляционную функцию помехи

m₁{ξ (t₁)ξ (t₂)} = Kξ (t) = G₀δ(τ),

где g₀ — спектральная плотность помехи; δ(τ) — дельта-функция;

τ= t2-t1

Тогда

Следовательно, среднеквадратическое значение погрешности восстановления

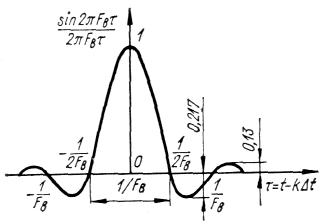
29. Функция отсчетов. Ее свойства.

Ряд Котельникова имеет вид:

(1-72)

Полученное выражение представляет собой разложение в ряд непрерывной функции х (t). Величины х (kΔt) представляют собой значения непрерывной функции в точках отсчета. Множитель вида (1-73)

является функцией времени и называется функцией отсчетов (рис. 7). Функция отсчетов принимает максимальное значение, равное единице, в моменты времени t = kΔt и обращается в нуль в моменты времени t = (k ±τ) Δt, где m = 1, 2, 3, .... Следует отметить, что функции отсчетов ортогональны на бесконечно большом интервале времени. Функция отсчетов представляет собой реакцию идеального фильтра нижних частот на единичную импульсную функцию.

30. Энтропия статистически зависимых сообщений.

При определении энтропии и количества передаваемой информации предполагалось, что элементы сообщений статистически независимы. Однако в реальных условиях независимость элементов сообщений — явление довольно редкое. Например, при передаче русского текста вероятности появления отдельных букв зависят от того, какие буквы им предшествовали. Например, если передана буква «п», вероятность того, что "следующей буквой может быть «а» гораздо больше, чем вероятность появления буквы «р». После буквы «ъ» никогда не ожидается появление буквы «н» и _т. п. Такая зависимость между элементами образовалась исторически в процессе длительного формирования современного русского языка.

Очевидно, что при определении энтропии и информации в сообщениях, элементы которых коррелированы, нельзя ограничиваться, как это мы делали до сих пор, только безусловными вероятностями элементов сообщений, необходимо учитывать и условные вероятности появления элементов.

Будем полагать, что передается конечное число сообщений х₁, х₂, х₃, ... , х_g, x_n, х_i, х_j, ... , х_п-1, х_п. Коррелятивные связи между элементами сообщений могут распространяться на различные группы элементов. Если элементы сообщений независимы, то условная вероятность передачи элемента Xj будет равна безусловной

р (x_j/x₁, x_n, х_g, ..., х₂, х₁) = р (х_j).

Если имеется коррелятивная связь только между двумя сосед­ними элементами, то вероятность передачи любого элемента сообщения будет зависеть лишь от того, каков был предшествующий символ, т. е. условная вероятность передачи элемента х_j будет равна p(Xj/Xi). В этом случае элементы сообщений составляют простую односвязную цепь Маркова.

Если коррелятивные связи охватывают три элемента сообщений то последние представляют двухсвязную цепь Маркова и услов ная вероятность передачи элемента хj будет равна р (xj/XiXn).

Большинство сообщений в реальных условиях представляю собой эргодическую последовательность, у которой коррелятивньн связи распространяются на конечное число элементов. При доста точной длине такой последовательности с достаточной точности могут быть определены вероятности и условные вероятности появ ления отдельных сообщений. Язык является типичным примере» такой последовательности. В любой книге на данном языке (кром узкоспециальных) частота повторения отдельных букв и их ра; личных сочетаний будет постоянной, независимой от содержани книги.

Пусть сообщения составляют простую, т. е. односвязную, цеп Маркова. В этом случае энтропия элемента х_j будет определятьс условной вероятностью р (Xj/xі).

Для данного фиксированного х_j энтропия сообщений буде определяться частной условной энтропией

Произведя усреднение по всем х_i, получим выражение для средней энтропии сообщения

В случае наличия коррелятивных связей между тремя элементами энтропия сообщений будет равна

Если коррелятивными связями охвачено большее число элементов, то энтропия определится аналогично.

При наличии коррелятивных связей между элементами энтропия сообщений, а следовательно, и количество передаваемой информации уменьшаются, причем это уменьшение будет тем интенсивнее, чем сильнее коррелятивные связи и чем большее число элементов будет охвачено этими связями.