10.3. Таблица неопределённых интегралов.

1	.	11	.
2	.	12	.
3	().	13	.
4	.	14	.
5	; .	15	.
6	.	16
7	.	17	.
8	.	18	.
9	.	19	.
10	.	20	; .

В формулах 14, 15, 16, 19 предполагается, что a>0. Каждая из формул таблицы справедлива на любом интервале, на котором непрерывна подынтегральная функция. Все эти формулы можно доказать дифференцированием правой части. Докажем, например, формулу 4: если x > 0, то ; если x < 0, то . Дальше мы докажем, что любая непрерывная функция имеет первообразную и, как следствие, неопределённый интеграл. При изучении дифференцирования было установлено, что с помощью таблицы производных и правил дифференцирования без труда можно получить производную любой элементарной функции, и эта производная тоже будет элементарной функцией. Операция интегрирования этим свойством не обладает: даже относительно простые функции могут иметь первообразные, которые через элементарные функции не выражаются. Так, доказано, что не берутся в элементарных функциях следующие интегралы, относящиеся к классу специальных функций: - интеграл Пуассона; , - интегралы Френеля; , , - интегральные синус, косинус, логарифм.

22

46

Линейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать.

Действительно, путь необходимо исследовать на экстремум линейную функцию

Z = С1х1+С2х2+... +СNxN

при линейных ограничениях

a11x1 + a22x2 + ... + a1NХN = b1

a21x1 + a22x2 + ... + a2NХN = b2

. . . . . . . . . . . . . . .

aМ1x1 + aМ2x2 + ... + aМNХN = bМ

 

Так как Z - линейная функция, то Z = Сj, (j = 1, 2, ..., n), то все коэффициенты линейной функции не могут быть равны нулю, следовательно, внутри области, образованной системой ограничений, экстремальные точки не существуют. Они могут быть на границе области, но исследовать точки границы невозможно, поскольку частные производные являются константами.

Для решения задач линейного программирования потребовалось создание специальных методов. Особенно широкое распространение линейное программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные.

Гл 1Математические основы решения задачи линейного программирования графическим способом

1.1 Математический аппарат

Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n =2 и n =3.

Наиболее наглядна эта интерпретация для случая n =2, т.е. для случая двух переменных и . Пусть нам задана задача линейного программирования в стандартной форме

(1.19)

39

Матрица в математике, система элементов a_ij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m ´ n)-матрице. Обозначения: 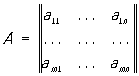   или . Короче:, . Наряду с конечными Матрица (в математике) рассматриваются Матрица (в математике) с бесконечным числом строк или столбцов.   Матрица (в математике), состоящая из одной строки, называется строкой, из одного столбца - столбцом. Если m = n, то Матрица (в математике) называется квадратной, а число n - её порядком. Квадратная Матрица (в математике), у которой отличны от нуля лишь диагональные элементы a_i = a_ii называется диагональной и обозначается diag(a₁, ..., a_n). Если все a_i = a, получают скалярную Матрица (в математике) При a = 1 Матрица (в математике) называется единичной и обозначается Е. Матрица (в математике), все элементы которой равны нулю, называется нулевой.   Переставив в Матрица (в математике) строки со столбцами, получают транспонированную Матрица (в математике) A’, или A^T. Если элементы Матрица (в математике) заменяют на комплексно-сопряжённые, получают комплексно-сопряжённую Матрица (в математике) А. Если элементы транспонированной Матрица (в математике) A’ заменяют на комплексно-сопряжённые, то получают Матрица (в математике) А*, называется сопряжённой с А. Определитель квадратной Матрица (в математике) А обозначается ½A½ или det A. Минором k-го порядка Матрица (в математике) А называется определитель k-го порядка, составленный из элементов, находящихся на пересечении некоторых k строк и k столбцов Матрица (в математике) A в их естественном расположении. Рангом Матрица (в математике) А называется максимальный порядок отличных от нуля миноров матрицы.   Действия над матрицами. Произведением прямоугольной (m ´ n)-матрицы А на число ее называют Матрица (в математике), элементы которой получены из элементов a_ij умножением на число a:     Сумма определяется для прямоугольных Матрица (в математике) одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, то есть 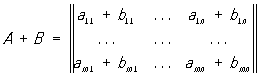    Умножение Матрица (в математике) определяется только для прямоугольных Матрица (в математике) таких, что число столбцов первого множителя равно числу строк второго. Произведением (m ´ р)-матрицы А на (р ´ n)-матрицу В будет (m ´ n)-матрица С с элементами   c_ij = a_i1b_1j + a_i2b_2j + ... + a_ipb_pj,   i = 1, ..., m,  j = 1, ..., n.   Введённые три действия над Матрица (в математике) обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении Матрица (в математике): равенство AB = BA может не выполняться. Матрицы А и В называются перестановочными, если AB = BA. Кроме того, произведение двух Матрица (в математике) может равняться нулевой Матрица (в математике), хотя каждый сомножитель отличен от нулевой. Справедливы правила:     Определитель произведения двух квадратных Матрица (в математике) равен произведению определителей перемножаемых Матрица (в математике)   Часто удобно разбивать Матрица (в математике) на клетки, являющиеся Матрица (в математике) меньших размеров, проводя разделительные линии через всю Матрица (в математике) слева направо или сверху вниз. При умножении такой так называемой клеточной Матрица (в математике) на число, нужно умножить все её клетки на то же число. При надлежащем согласовании разбиений действия сложения и умножения клеточных Матрица (в математике) осуществляются так, как будто вместо клеток стоят числа.   Квадратная Матрица (в математике) А = (a_ij) называется неособенной, или невырожденной, если её определитель не равен нулю; в противном случае Матрица (в математике) называется особенной (вырожденной). Матрица (в математике) А^-1 называется обратной к квадратной Матрица (в математике) А, если AA^-1 = E, при этом . Неособенность Матрица (в математике) А есть необходимое и достаточное условие существования обратной Матрица (в математике), которая при этом оказывается единственной и перестановочной с исходной Матрица (в математике) Верна формула: (AB)^-1 = B^-1A^-1.   Большой интерес приобретает обобщённая обратная (или псевдообратная) Матрица (в математике) А⁺, определяемая как для любой прямоугольной Матрица (в математике), так и для особенной квадратной. Эта Матрица (в математике) определяется из четырёх равенств:   AA⁺A = A, А⁺АА⁺ = А, AA⁺ = (AA⁺)*, А⁺А = (А⁺А)*.   Квадратные матрицы. Степенью Aⁿ Матрица (в математике) А называется произведение n сомножителей, равных А. Выражение вида a₀Аⁿ + a₁A^n-1 + ... + a_nE, где a₀, a₁, ..., a_n - числа, называется значением полинома a₀tⁿ + a_it^n-1 + ... + a_nE от квадратной Матрица (в математике) А. Правила действий над полиномами от данной Матрица (в математике) А ничем не отличаются от правил действий над алгебраическими многочленами. Можно рассматривать и аналитические функции от Матрица (в математике) В частности, если   есть сходящийся на всей комплексной плоскости ряд (например, ), то и бесконечный ряд  оказывается сходящимся при любой Матрица (в математике) А, его сумму естественно считать равной f(A). Если же ряд f(t) сходится в некотором конечном круге сходимости, то f(A) задаётся этим рядом для достаточно «малых» Матрица (в математике)   Аналитические функции от Матрица (в математике) играют большую роль в теории дифференциальных уравнений. Так, система обыкновенных дифференциальных уравнений с постоянными коэффициентами, записанных в матричных обозначениях в виде   (здесь Х - столбец из неизвестных функций), имеет решение х = e^AtC, где С - столбец из произвольных постоянных.   Ненулевой столбец Х такой, что AX = lХ, называется собственным вектором Матрица (в математике) А. В этом равенстве коэффициент l может быть лишь одним из корней многочлена 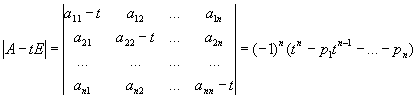  который называется характеристическим многочленом Матрица (в математике) А. Эти корни называются собственными значениями, или характеристическими числами, Матрица (в математике) А. Коэффициенты характеристического многочлена выражаются через суммы некоторых миноров Матрица (в математике) А. В частности, p₁ = a₁₁ + ... + a_1n = SpA (след A), . Справедливо соотношение Кэли - Гамильтона: если j(f) есть характеристический многочлен Матрица (в математике) А, то j(A) = 0, так что Матрица (в математике) А является «корнем» своего характеристического многочлена.   Матрица (в математике) А называется подобной Матрица (в математике) В, если существует такая неособенная Матрица (в математике) С, что В = С^-1AС. Легко проверяется, что подобные Матрица (в математике) имеют одинаковые характеристические многочлены.   Исчисление матриц. Матрица (в математике) - полезный аппарат для исследования многих задач теоретической и прикладной математики. Одной из важнейших задач является задача нахождения решения систем линейных алгебраических уравнений. В матричных обозначениях такие системы записываются в виде   AX = F, где A есть Матрица (в математике) коэффициентов, Х - искомое решение, записанное в виде столбца из n элементов, F - столбец свободных членов из m элементов. Если А - квадратная неособенная Матрица (в математике), то система имеет единственное решение Х = A ^-1F. Если A прямоугольная (m ´ n-матрица ранга k, то решение может не существовать или быть не единственным. В случае несуществования решения имеет смысл обобщённое решение, дающее минимум сумме квадратов невязок (см. Наименьших квадратов метод). При отсутствии единственности точного или обобщённого решения часто выбирают нормальное решение, то есть решение с наименьшей суммой квадратов компонент. Нормальное обобщённое решение находится по формуле Х = A + F. Наиболее важен случай переопределённой системы: k = n < m. В этом случае обобщённое решение единственно. При k = m < n (недоопределённая система) точных решений бесконечно много и формула даёт нормальное решение.

32

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов , обозначается символом (порядок записи сомножителей безразличен, то есть ).

Если угол между векторами , обозначить через , то их скалярное произведение можно выразить формулой

(1)

Скалярное произведение векторов , можно выразить также формулой

, или .

Из формулы (1) следует, что , если - острый угол, , если - тупой угол; в том и только в том случае, когда векторы и перпендикулярны (в частности, , если или ).

Скалярное произведение называется скалярным квадратом вектора и обозначается символом . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:

.

Если векторы и заданы своими координатами:

, ,

то их скалярное произведение может быть вычислено по формуле

.

Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов

.

Угол между векторами

, ,

дается формулой 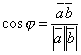, или в координатах

26

Определение. Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.      Пример. Найти общее решение уравнения y'+3y=e^2x и частное решение,удовлетворяющее начальным условиям х=0, у=1.      Решение. Данное уравнение является линейным.      Здесь ρ(x)=3 и f(x)=e^2x.      Решение ищем в виде y=U∙υ, где U и υ – некоторые функции от х. Находим y'= U'υ+ Uυ' и подставляем в уравнение значение y и y', получаем: U'υ+Uυ'+3Uυ=e^{2 x} или U'υ+U(υ'+3υ)= e^2x.      Найдем одно значение υ, при котором выражение в скобках, обращается в нуль: υ'+3υ=0. Получим уравнение с разделяющимися переменными. Решая его получаем:    ln υ =–3x,υ=e^–3x.      Подставляем найденное значение υ в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:      .      Итак, общее решение данного уравнения имеет вид:      .      Найдем частное решение. Для этого подставим  начальные условия в выражение для общего решения и найдем С.      .      Частное решение имеет вид:

27

Уравнение вида y''+ρy'+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.      Рассмотрим линейное уравнение второго порядка вида:      y''+ρy'+qy=0,                                                      (1)      у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.      Уравнение      K²+ρK+q=0                                             (2)      называется характеристическим уравнением данного уравнения (1).      Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К₁ и К₂.      Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ²–4q уравнения (2) следующим образом:      1. При D>0 корни характеристического уравнения вещественные и различные (К₁≠К₂), и общее решение имеет вид .      2. При D=0 корни характеристического уравнения вещественные и равные (К₁=К₂=К), и общее решение имеет вид:      3. Если D<0, то корни характеристического уравнения комплексные: , где  – мнимая единица,  и общее решение (К₁=α+βi, К₂=α–βi, β≠0), имеет вид y=e^αx(C₁ cosβx+C₂ sinβx).      Пример 1. Найти общее уравнение y''–y'–2y=0.      Решение. Характеристическое уравнение имеет вид K²–K–2=0, его корни К₁=1, К₂=–2 вещественные и различные. Общее решение уравнения имеет вид y=C₁e^x+C₂e^–2x.

33