
1
Множество и элемент множества относятся к числу первичных понятий, для которых не существует определений в строгом смысле слова. Поэтому обычно говорят о множестве как о наборе предметов ( элементов множества ), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли – всё это примеры множеств.
Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.
Пустое
множество ( ![]() ) не
содержит ни одного элемента, например,
множество крылатых слонов, множество
корней уравнения sin x =
2 и т.д.
) не
содержит ни одного элемента, например,
множество крылатых слонов, множество
корней уравнения sin x =
2 и т.д.
Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множествоточек плоскости, множество атомов во Вселенной и т.д.
Счётное множество – множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке ) или бесконечным ( множество целых чисел, его элементы можно пронумеровать следующим образом:
элементы множества: …, –5, – 4, –3, –2, –1, 0, 1, 2, 3, 4, 5, …
номера элементов: ... 11 9 7 5 3 1 2 4 6 8 10 ... ) .
Несчётное множество – множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным (продумайте, почему ? ).
Выпуклое множество – множество, которое наряду с любыми двумя точками А и В содержит также весь отрезок АВ. Примеры выпуклых множеств: прямая, плоскость, круг. Однако, окружностьне является выпуклым множеством.
Способы задания множеств. Множество может быть задано следующим образом:
– перечислением всех его элементов по их названиям ( так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);
– заданием общей характеристики ( общих свойств ) элементов данного множества ( например, множество рациональных чисел, собаки, семейство кошачих и т.д.);
– формальным законом построения элементов множества ( например, формула общего члена числовой последовательности, Периодическая система элементов Менделеева и т.д.).
2
Множества
обозначаются заглавными латинскими
буквами, а их элементы – строчными.
Запись a ![]() R означает,
что элемент а принадлежит
множеству R ,
то есть а является
элементом множества R .
В противном случае, когда а не
принадлежит множеству R ,
пишут a
R означает,
что элемент а принадлежит
множеству R ,
то есть а является
элементом множества R .
В противном случае, когда а не
принадлежит множеству R ,
пишут a ![]() R .
R .
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
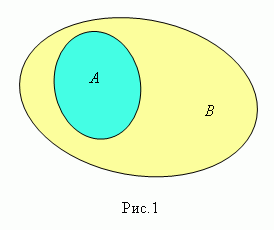
Говорят,
что множество А содержится
в множестве В ( рис.1 )
или множество А является подмножеством множества В ( в
этом случае пишут А ![]() В ), если
каждый элемент множества Аодновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения:
В ), если
каждый элемент множества Аодновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения: ![]()
![]() А
и А
А
и А ![]() А .
А .
Сумма
( объединение )
множеств А и В ( пишется А ![]() В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либо В.
Таким образом, е
В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либо В.
Таким образом, е ![]() А
А ![]() В тогда
и только тогда, когда либо
е
В тогда
и только тогда, когда либо
е ![]() А , либо е
А , либо е ![]() В .
В .
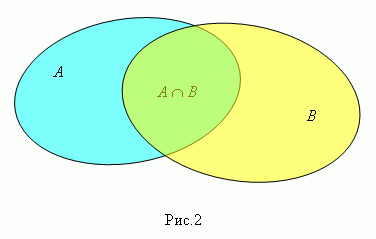
Произведение
( пересечение )
множеств А и В ( пишется А ![]() В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит и А ,
и В .
Таким образом, е
В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит и А ,
и В .
Таким образом, е ![]() А
А ![]() В тогда
и только тогда, когда е
В тогда
и только тогда, когда е ![]() А и е
А и е ![]() В .
В .
Разность множеств А и В ( пишется А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется такжедополнением множества В относительно множества А.

Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В ) ![]() ( В – А ).
( В – А ).
Свойства операций над множествами:

3
Отношением (бинарным
отношением, двуместным отношением) из
множества A в
множество B называется
некоторое подмножество декартового
произведения ![]()
Отношения
в дальнейшем будем обозначать ![]()
![]()
(читается ![]() отношение
из A в B)
отношение
из A в B)
Если ![]() ,
, ![]() и
и ![]() ,
то говорят, что a находится
в отношении с b.
Используется также запись
,
то говорят, что a находится
в отношении с b.
Используется также запись
![]()
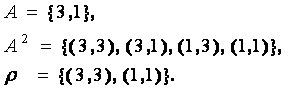
n-арным отношением на множестве А, называется некоторое подмножество n-ой степени множества A.
Виды бинарных отношений на множестве A
1) Обратное
отношение ![]() .
.
2) Дополнение ![]() .
.
3) Тождественные ![]() .
.
4) Универсальные ![]() .
.
40
Равенство
матриц. Две матрицы ![]() и
и ![]() одинакового
размера m на nназываются равными,
если
одинакового
размера m на nназываются равными,
если ![]() , i
= 1,2,…,m, j=1,2,…,n.
, i
= 1,2,…,m, j=1,2,…,n.
Если матрицы A и B равны, то будем писать A=B.
Линейные
операции. Суммой двух матриц A и B размера m
на n называется
матрица C
размера m на n, элементы
которой определяются равенством![]()
Сумму матриц A и B будем обозначать C=A+B.
Матрица ![]() называется противоположной к
матрице
называется противоположной к
матрице ![]() .
.
Теорема
2.1 Операция сложения
матриц обладает
следующими свойствами: для любых
матриц ![]() и
нулевой матрицы
и
нулевой матрицы ![]()
1) A+B=B+A; (перестановочность или коммутативность операции сложения
2) (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)
3) A+O = O+A =A;
4) A+(-A)=(-A)+A=O.
Перечисленные выше свойства непосредственно вытекают из определения и доказываются по единой схеме.
Разностью
матриц ![]() и
и ![]() называется
матрица A+(-B).
называется
матрица A+(-B).
Разность матриц A и B будем обозначать A-B.
Произведением
матрицы ![]() на
число
на
число ![]() называется
матрица
называется
матрица![]() ,
элементы которой определены равенством
,
элементы которой определены равенством![]()
Произведение
матрицы A на
число ![]() будем
обозначать
будем
обозначать ![]() .
.
Теорема 2.2 Операция умножения матрицы на число обладает следующими свойствами:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() (Распределительное
свойство относительно сложения матриц);
(Распределительное
свойство относительно сложения матриц);
4) ![]() (Распределительное
свойство относительно сложения чисел);
(Распределительное
свойство относительно сложения чисел);
5) -A=(-1)A.
Все перечисленные свойства непосредственно вытекают из определения.
Операции
сложения матриц и умножения матрицы на
число позволяют для произвольных
матриц ![]() одинакового
размера
одинакового
размера ![]() и
произвольных чисел
и
произвольных чисел ![]() однозначно
определить матрицу
однозначно
определить матрицу 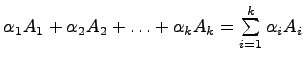 ,
называемуюлинейной
комбинацией матриц
,
называемуюлинейной
комбинацией матриц ![]() с
коэффициентами
с
коэффициентами ![]() .
.
Умножение
матриц. Произведением матриц ![]() и
и ![]() называется
матрица
называется
матрица ![]() ,
элементы которой определены равенством
,
элементы которой определены равенством
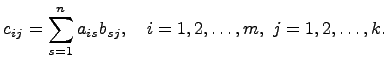
Произведение матриц A и B будем обозначать C=AB.
Из
определения следует, что
произведение AB определено
лишь в том случае, когда число столбцов
матрицы A
совпадает с числом строк матрицы B. Это
означает, что оба произведения AB
и BA определены
тогда и только тогда, когда матрицы
A и B имеют размеры ![]() и
и ![]() соответственно.
Следовательно равенство AB=BA возможно
лишь для квадратных
матриц одинакового порядка. Однако
и в этом случае произведение матриц,
вообще говоря, зависит от порядка
сомножителей.
соответственно.
Следовательно равенство AB=BA возможно
лишь для квадратных
матриц одинакового порядка. Однако
и в этом случае произведение матриц,
вообще говоря, зависит от порядка
сомножителей.
Матрицы A и B называются перестановочными или коммутирующими, если AB=BA.
Теорема 2.3 Операция умножения матриц обладает следующими свойствами:
1) (AB)C=A(BC); (Свойство ассоциативности)
2) ![]() ,
для любого действительного числа
,
для любого действительного числа ![]()
3) A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности), для любых матриц A, B, C,для которых левые части равенств имеют смысл.
8
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.
Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать.
Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы.
Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, ..., хn с соответствующими им вероятностями р1, р2, ..., рn
16
Определение 2.11 Первым замечательным пределом называется предел
![]()
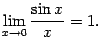 и
и 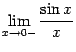 также
будет равняться 1.
также
будет равняться 1.
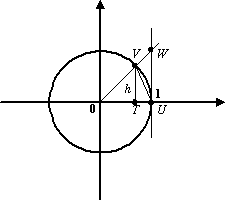
Итак,
пусть ![]() ).
В тригонометрическом круге
(радиуса
).
В тригонометрическом круге
(радиуса ![]() построим
центральный угол, равный
построим
центральный угол, равный ![]() пересечения
горизонтальной оси с окружностью (
пересечения
горизонтальной оси с окружностью (![]() с
окружностью буквой
с
окружностью буквой ![]() ;
через
;
через ![]() на
горизонтальную ось.
на
горизонтальную ось.
18
Путь x – аргумент функции f(x) и - малое число, отличное от нуля.
(читается «дельта икс») называют приращением аргумента функции. На рисунке красной линией показано изменение аргумента от значения x до значения (отсюда видна суть названия «приращение» аргумента).
При переходе от значения аргумента к значения функции изменяются соответственно от до при условии монотонности функции на отрезке . Разность называют приращением функции f(x), соответствующем данному приращению аргумента. На рисунке приращение функции показано синей линией.
Определение производной функции в точке.
Пусть функция f(x) определена на промежутке (a; b), и - точки этого промежутка. Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при . Обозначается .
Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.
Функцию f(x) называют дифференцируемой в точке , когда она имеет в ней конечную производную.
Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке , то есть, мы имеем возможность определить новую функцию , которую называют производной функции f(x) на интервале (a; b).
13
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
![]() .
.
Доказательство.
Проведем доказательство для двух
слагаемых, так как для любого числа
слагаемых оно проводится так же.
Пусть ![]() .Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
.Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то
![]()
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
![]() .
.
Доказательство.
Пусть ![]() .
Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть
величина постоянная. Функция bβ
+ c α + αβ на
основании свойств бесконечно малых
функций есть величина бесконечно малая.
Поэтому ![]() .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
![]() .
.
Следствие 2. Предел степени равен степени предела:
![]() .
.
Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если
![]() ,
то
,
то ![]() .
.
Смысл этой теоремы понятен из рисунка.
Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.
Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.
Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.
Теорема
6. Если
две функции f(x) и g(x) при
всех значениях аргумента x удовлетворяют
неравенству f(x)≥
g(x) и
имеют пределы ![]() ,
то имеет место неравенство b≥c.
,
то имеет место неравенство b≥c.
43
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим
матрицу системы 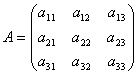 и
матрицы столбцы неизвестных и свободных
членов
и
матрицы столбцы неизвестных и свободных
членов 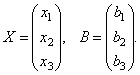
Найдем произведение
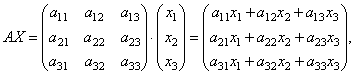
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
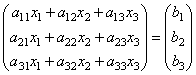 или
короче A∙X=B.
или
короче A∙X=B.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть
определитель матрицы отличен от нуля
|A|
≠ 0. Тогда матричное уравнение решается
следующим образом. Умножим обе части
уравнения слева на матрицу A-1,
обратную матрице A: ![]() .
Поскольку A-1A
= E и E∙X
= X,
то получаем решение матричного уравнения
в виде X
= A-1B.
.
Поскольку A-1A
= E и E∙X
= X,
то получаем решение матричного уравнения
в виде X
= A-1B.
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A-1B.
6
Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.
Теорема сложения вероятностей
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
В случае, когда события А и В совместны, вер-ть их суммы выражается формулой
Р (А +В) = Р (А) + Р (В) – Р (АВ),
где АВ – произведение событий А и В.
Два события называются зависимыми, если вероятность одного из них зависит от наступления или не наступления другого. в случае зависимых событий вводится понятие условной вероятности события.
Условной вероятностью Р(А/В) события А называется вероятность события А, вычисленная при условии, что событие В произошло. Аналогично через Р(В/А) обозначается условная вероятность события В при условии, что событие А наступило.
Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В.
Теорема умножения вероятностей
Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого:
Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В).
Следствие. Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей этих событий:
Р (АВ) = Р(А) · Р(В).
Следствие. При производимых n одинаковых независимых испытаниях, в каждом из которых событияА появляется с вероятностью р, вероятность появления события А хотя бы один раз равна 1 - (1 - р)n
10
|
Если каждому числу n натурального ряда чисел 1, 2, ..., n, ... ставится в соответствие по определенному закону некоторое вещественное число xn, то множество вещественных чисел x1, x2, x3, ..., xn мы назовем числовой последовательностью или просто последовательностью. Сокращенно последовательность обозначается - {xn}. |
|
|
|
|
[Править]Задание последовательностей
Чтобы понять смысл слов: „по определенному закону“ ниже на примерах показано, как могут
задаваться последовательности ("законы" выделены жирным шрифтом):
1, 2, 3, 4, 5, 6, ..., n,... - последовательность натуральных чисел.
2, 4, 6, 8, 10, ..., 2n ,... - последовательность чётных чисел.
1, 3, 5, 7, 9, ..., 2n+1 , ... - последовательность нечётных чисел.
3,14;
3,141; 3,1415; 3,14159; ...; 3,1415926535897932384626433832; ...;  ;
... - последовательность приближённых
значений числа π с увеличивающейся
точностью.
;
... - последовательность приближённых
значений числа π с увеличивающейся
точностью.
В общем виде последовательности задаются в виде функции, являясь результатом их вычисления.
15
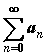 ,an>
0 .
Признак
Даламбера:
,an>
0 .
Признак
Даламбера: 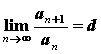 ,
, ![]() ,
если d <1 —
ряд сходится, если d >1 —
ряд расходится,
если d =1 —
о сходимости или расходимости ряда
судить нельзя.
Признак
Коши:
,
если d <1 —
ряд сходится, если d >1 —
ряд расходится,
если d =1 —
о сходимости или расходимости ряда
судить нельзя.
Признак
Коши: ![]() ,
, ![]() ,
если c <1 —
ряд сходится, если c >1 —
ряд расходится,
если c =1 —
о сходимости или расходимости ряда
судить нельзя.
Знакочередующийся
ряд:
,
если c <1 —
ряд сходится, если c >1 —
ряд расходится,
если c =1 —
о сходимости или расходимости ряда
судить нельзя.
Знакочередующийся
ряд: 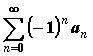 ,
, ![]() .
Если
сходится ряд
.
Если
сходится ряд 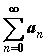 ,
то ряд
,
то ряд 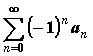 —
сходится а
б с о л ю т н о.
Если
ряд
—
сходится а
б с о л ю т н о.
Если
ряд  расходится,
а ряд
расходится,
а ряд 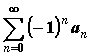 сходится,
то знакочередующийся ряд
сходится,
то знакочередующийся ряд
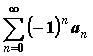 —
сходится у
с л о в н о.
Признак
Лейбница:
если an монотонно
убывая стремится к нулю, то ряд
—
сходится у
с л о в н о.
Признак
Лейбница:
если an монотонно
убывая стремится к нулю, то ряд 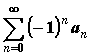 сходится
и
сходится
и
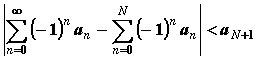 .
.
11
Определение.
Пусть каждому
натуральному числу n
поставлено в соответствие некоторое
единственное действительное число![]() (при этом разным натуральным числам n
могут соответствовать и одинаковые
действительные числа). В этом случае на
множестве натуральных чисел определена
функция:
(при этом разным натуральным числам n
могут соответствовать и одинаковые
действительные числа). В этом случае на
множестве натуральных чисел определена
функция:
![]() ,
которая называется числовой
последовательностью или просто
последовательностью.
,
которая называется числовой
последовательностью или просто
последовательностью.
Последовательность
обозначается:
![]() ,
n=1, 2,… или
,
n=1, 2,… или
![]() .
.
Числа
![]() ,
,
![]() ,…
называются членами последовательности
или ее элементами,
,…
называются членами последовательности
или ее элементами,
![]() –
общим членом последовательности, n
– номером
члена
–
общим членом последовательности, n
– номером
члена
![]() .
.
По определению любая последовательность содержит бесконечное множество элементов.
Часто
последовательность задается при помощи
формулы:
![]() ,
,
![]() .
В этом случае эта формула называется
формулой общего члена последовательности
{
.
В этом случае эта формула называется
формулой общего члена последовательности
{![]() }.
Например,
}.
Например,
![]() =
=![]() ,
,![]() ;
;
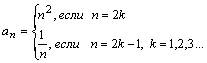
Последовательность
может быть задана и другими способами.
Например, если
![]() –
число всех различных делителей числа
n,
то
–
число всех различных делителей числа
n,
то
![]() ,
,
![]() -
последовательность, для которой
-
последовательность, для которой
![]() =1,
=1,
![]() =2,
=2,
![]() =2,
=2,
![]() =3,
=3,
![]() =2,
=2,
![]() =4,
=4,
![]() =2,…
=2,…
Для задания последовательностей используют также рекуррентные соотношения. При таком способе задания последовательности указывают один или несколько первых ее членов и формулу, которая позволяет найти ее n-й член через предшествующие члены. Например,
a![]() =1,
a
=1,
a![]() =
=
![]() +1
при n=1,
2,…;
+1
при n=1,
2,…;
b![]() =1,
b
=1,
b![]() =2,
b
=2,
b![]() =2b
=2b![]() +b
+b![]() при n
при n![]() 3.
3.![]()
Определение.
Пусть даны
две числовые последовательности {a![]() }
и {b
}
и {b![]() }.
Суммой, разностью, произведением и
частным этих последовательностей
называются соответственно последовательности
{
}.
Суммой, разностью, произведением и
частным этих последовательностей
называются соответственно последовательности
{![]() }, {
}, {![]() }, {
}, {![]() },
{
},
{![]() };
последнее при условии, b
};
последнее при условии, b![]()
![]() 0,
n=1, 2,….
Произведением последовательности {a
0,
n=1, 2,….
Произведением последовательности {a![]() }
на число k,
называется последовательность {ka
}
на число k,
называется последовательность {ka![]() }.
}.
Определение.
Последовательность
{a![]() }
называется возрастающей (убывающей),
если для любого n
}
называется возрастающей (убывающей),
если для любого n![]() N
справедливо неравенство a
N
справедливо неравенство a![]() >a
>a![]() (a
(a![]() <a
<a![]() ).
Последовательность {a
).
Последовательность {a![]() }
называется неубывающей (невозрастающей),
если для любого n
}
называется неубывающей (невозрастающей),
если для любого n![]() N
справедливо неравенство a
N
справедливо неравенство a![]()
![]() a
a![]() (a
(a![]()
![]() a
a![]() ).
).
Определение.
Последовательности
убывающие, возрастающие, неубывающие,
невозрастающие называются монотонными
последовательностями. Например, а)
последовательность a![]() =n!,
n
=n!,
n![]() N
– возрастающая;
б) последовательность 1, 2, 3, 3, 4, 5, 6, 6, 7,
8, 9, 9,…- неубывающая; в) последовательность
1,
N
– возрастающая;
б) последовательность 1, 2, 3, 3, 4, 5, 6, 6, 7,
8, 9, 9,…- неубывающая; в) последовательность
1,
![]() ,
3,
,
3,
![]() ,
5,
,
5,
![]() ,
7,
,
7,
![]() ,…
– немонотонная.
,…
– немонотонная.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
