
UMK11
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Государственное образовательное учреждение высшего профессионального образования
"УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ" (УГНТУ)
Кафедра математики
УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС
дисциплины «Математика»
________________________________________________________________________________
РАЗДЕЛ 11 «ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ»
Теоретические основы Методические указания для студентов Материалы для самостоятельной работы студентов
Уфа 2010

ИНФОРМАЦИЯ ОБ АВТОРАХ ИНФОРМАЦИЯ О РЕЦЕНЗЕНТАХ АННОТАЦИЯ
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
1.1. Комплексные числа и действия над ними 1.2. Модуль и аргумент комплексного числа. Свойства
1.3. Свойства модулей и аргумента. Деление комплексных чисел. Степень комплексного числа. Извлечение корня из комплексного числа
1.4. Комплексная переменная и ее предел
1.5. Дифференцируемость ФКП. Понятие аналитической функции в точке и в области
1.6. Интегрирование ФКП. Теорема Коши. Основные формулы теории интегрирования аналитических функций
1.7. Интегральная формула Коши. Следствия. Примеры 1.8. Комплексные числовые ряды. Комплексные функциональные
ряды 1.9. Степенные комплексные ряды
1.10. Понятие ряда Лорана. Теорема Лорана 1.11. Нули аналитической функции и их связь с полюсами
1.12. Применение вычетов к вычислению определенных и несобственных интегралов 2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ
2.1. Комплексные числа и действия над ними 2.2. Множество точек, линии, области на комплексной
плоскости 2.3. Функция комплексного переменного. Предел и
непрерывность функции. Основные элементарные функции 2.4. Производная функции комплексного переменного. Условия
дифференцируемости. Аналитические функции. Понятие о конформном отображении
2.5. Интегрирование функции комплексного переменного
2.6. Ряды в комплексной области
2.7. Изолированные особые точки функции комплексного переменного
2.8. Вычеты и их применение к вычислению контурных интегралов
3. МАТЕРИАЛЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

3.1. Контрольные вопросы 3.2. Задачи и упражнения для самостоятельной работы 3.3. Расчетные задания
ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
1.1. Преобразование Лапласа. Оригинал и изображение 1.2. Простейшие свойства и теоремы об изображениях.
Иллюстративные примеры 2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ
2.1. Примеры нахождения изображения по оригиналу
2.2. Примеры нахождения оригинала по изображению 2.3. Операторный метод интегрирования линейных
дифференциальных уравнений (ЛДУ) с постоянными коэффициентами
3. МАТЕРИАЛЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
3.1. Контрольные вопросы 3.2. Задачи и упражнения для самостоятельной работы 3.3. Расчетные задания
Список литературы
АВТОРЫ:
Бахтизин Р.Н., Степанова М.Ф., Яфаров Ш.А., Шамшович В.Ф., АкмадиеваТ.Р., Аносова Е.П., Байрамгулова Р.С., Галиуллин М.М., Галиева Л.М., Галиакбарова Э.В., Гимаев Р.Г., Гудкова Е.В., Егорова Р.А., Жданова Т.Г., Зарипов Э.М., Зарипов Р.М., Исламгулова Г.Ф., Ковалева Э.А., Майский Р.А., Мухаметзянов И.З., Нагаева З.М., Савлучинская Н.М.,
Сахарова |
Л.А., |
Сокова И.А., |
Сулейманов |
И.Н., |
Умергалина Т.В., |
Фаткуллин |
Н.Ю., |
Хайбуллин |
Р.Я., Хакимов |
Д.К., |
Хакимова З.Р., |
Чернятьева М.Р., Юлдыбаев Л.Х., Якубова Д.Ф., Якупов В.М., Янчушка А.П. 8 – (347)2428715
E-mail: kafedra-matematiki@rambler.ru
РЕЦЕНЗЕНТЫ:
Кафедра программирования и вычислительной математики Башкирского государственного педагогического университета.
Заведующий кафедрой д. ф.-м. наук, профессор Р.М. Асадуллин.
Кафедра вычислительной математики Башкирского государственного университета.
Заведующий кафедрой д. ф.-м. наук, профессор Н.Д. Морозкин.
АННОТАЦИЯ
Учебно-методический комплекс дисциплины «Математика». Раздел 11 «Теория функций комплексного переменного. Элементы операционного исчисления». Теоретические основы. Методические указания для студентов. Материалы для самостоятельной работы студентов.
В разделе «Теоретические основы» и «Методические указания для студентов» содержатся необходимые для изучения дисциплины «Математика», в объеме, предусмотренном ГОС для технических вузов, теоретический материал, способы и методы решения практических задач.
Раздел «Материалы для самостоятельной работы студентов» включает в себя: контрольные вопросы, задачи и упражнения для самостоятельной работы, расчетные задания, лабораторные работы, литературу.
Представлен перечень контрольных вопросов для контроля знаний, полученных студентами при изучении теоретических и методических основ дисциплины. Задачи и упражнения для самостоятельной работы студентов позволяют учащимся индивидуально во внеурочное время контролировать уровень усвоения материала по данной дисциплине.
Расчетные задания содержат задания для студентов, позволяющих отработать навыки решения задач практического содержания.
В разделе «Лабораторная работа» представлен теоретический материал, последовательность проведения лабораторной работы и данные для проведения лабораторной работы по вариантам.
При изучении дисциплины обеспечивается фундаментальная подготовка студента в области применения математики, происходит знакомство со стержневыми проблемами прикладной математики, базовыми приложениями, навыками и понятиями, обязательными для прочного усвоения последующих дисциплин и практического использования полученных знаний в решении конкретных задач, которые ставятся перед инженером.
Учебно-методический комплекс разработан для студентов, обучающихся по всем формам обучения по направлениям подготовки и специальностям, реализуемым в ГОУ ВПО УГНТУ.
© Уфимский государственный нефтяной технический университет, 2010
УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС
РАЗДЕЛ 11 «ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ»
1. Теоретические основы
1.1. КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
ОПРЕДЕЛЕНИЕ 1.1. Комплексным числом (КЧ) называется упорядоченная пара вещественных (действительных) чисел. Множество КЧ обозначается через С:
С = {(x, y) |
|
x, y R}. |
(1.1) |
|
В этом множестве сразу же определим равенство КЧ, а именно:
x |
|
= x |
|
|
|
|
(x1 , y1 ) = (x2 , y 2 ) |
1 |
|
2 |
|
|
(1.2) |
y1 |
= y 2 . |
|
|
|
||
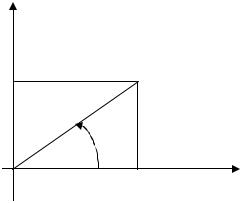
На плоскости введем декартову пря- |
|
y |
|
|
||
моугольную систему координат и каждому |
|
|
|
|||
КЧ (x, y) поставим в соответствие точку с |
|
|
|
|
||
координатами (x, y) (рис.1.1). Это соот- |
|
y |
∙ z(x, y) |
|||
ветствие биективно (взаимнооднозначно) и |
|
|
||||
|
|
|
|
|||
дает изображение КЧ. |
, |
|
|
|
|
|
Из (1.2) следует: два КЧ равны |
|
|
ϕ |
|
||
когда их изображения совпадают. |
|
|
|
|
|
|
ОПРЕДЕЛЕНИЕ 1.2. Плоскость, на |
|
0 |
x |
x |
||
|
|
|
|
|||
которой введена декартова прямоугольная |
|
|
Рис. 1.1 |
|
||
система координат для изображения ком- |
|
|
|
|||
|
|
|
|
|||
плексных чисел, называется комплексной |
|
|
|
|
||
плоскостью.
Обратим внимание на то, что это есть обычная плоскость с введенной на ней прямоугольной декартовой системой координат. Термин «комплексная» возникает из-за того, что на ней изображаются комплексные числа.
На множестве С введем две (алгебраические) операции: сумма и произведение.
Сумма определяется так: С× С → С, то есть каждой упорядоченной паре (x1 , y1 ) и (x 2 , y2 ) элементов из C поставим в соответствие новый элемент из C по правилу:
(x1 , y1 )± (x2 , y 2 ) = (x1 ± x2 ;y1 ± y 2 ), |
(1.3) |
то есть имеет место покоординатное суммирование. Например, (1,0) + (0,1) = = (1,1); (3,7) − (7,4) = (− 4,3). КЧ (x, y) обозначим через z , полагая
z = (x, y ), |
(1.4) |
при этом первая составляющая x называется вещественной частью КЧ z и
обозначается |
Re z ; вторая составляющая y называется мнимой частью z и |
|
обозначается |
Jm z . Таким образом, x = Re z, |
y = Jm z . |
Сразу обратим внимание читателя на то, что Re z и Jm z есть вещественные (действительные) числа.
И через z же будем обозначать изображение КЧ z , чтобы не вводить новых букв и не загромождать текст (см. рис. 1.1).
Непосредственно проверяется, что операция «+» обладает свойствами: 1.10. Коммутативность (переместительность). z1 , z 2 C
z1 + z 2 = z 2 + z1 .
1.20. Ассоциативность. z1 , z 2 , z3 C z1 + (z 2 + z3 )= (z 2 + z1 )+ z3 .
Легко проверяется, что пара (0,0) играет роль нуля.
Вторая из операций – умножение КЧ: C ×C = C2 → C . Предметно это
выглядит так: если z1 = (x1 , y1 ), z 2 = (x 2 , y2 ), то |
|
z1 = (x1 , y1 )× (x2 , y 2 )= (x1x2 - y1 y 2 ;x1 y 2 + x2 y1 ) |
(1.5) |
Если наряду с суммой на некотором множестве M определяется операция умножения: M × M → M ( упорядоченной паре элементов из M ставится в соответствие вполне определенный элемент из M ), то говорят, что имеет место алгебра. (На M введена алгебраическая структура.) Если операция умножения обладает еще распределительными свойствами, то говорят, что имеет место линейная алгебра.
Примером линейной алгебраической структуры (антикоммутативная линейная алгебра) является трехмерное векторное пространство, где операция умножения есть векторное произведение двух векторов. Обратим внимание читателя на то, что об алгебраической структуре на M можно говорить тогда и только тогда, когда на M введена операция суммы.
Убедимся, что в нашем случае алгебра КЧ коммутативна, то есть
1.30. z1 z 2 = z 2 z1 . |
(1.6) |
Всамом деле, z 2 z1 = (x 2 , y2 )(x1 , y1 )= (x 2 x1 − y2 y1 ; x 2 y1 + x1 y2 )=
=(x1x 2 − y1 y2 ; x1 y2 + x 2 y1 )= z1z 2 согласно (1.5). Аналогично проверяется,
что произведение КЧ удовлетворяет еще следующим условиям.
(z1z 2 )z3 = z1 (z 2 z3 )− ассоциативное свойство умножения.
1.50. (z1 + z 2 )z3 = z1z3 + z 2 z3 − распределительное свойство относи-
тельно первого множителя.
(z 2 + z3 )z1 = z1z 2 + z1z3 − распределительное свойство относительно второго множителя.
1.60. Роль единицы выполняет упорядоченная пара (1,0), так как для
z C
z (1,0)= (1, 0)z = (1,0)(x, y)= (x, y).
Таким образом, операция умножения КЧ приводит к линейной алгебре.

1.2. МОДУЛЬ И АРГУМЕНТ КОМПЛЕКСНОГО ЧИСЛА.
СВОЙСТВА |
|
Введем стандартные обозначения (рис. 1.1): |
|
arg z = ϕ − угол, который образует вектор 0z ( z − изображение КЧ |
|
z = (x, y)) с осью (0x), если ϕ (− π; π], |
|
z = 0z = x 2 + y2 - модуль КЧ z . Отсюда видно, |
что z определяет |
расстояние от точки z до начала координат. В силу этого |
z ³ 0 , при этом |
z = 0 Û z = (0,0), аргумент последнего не определяется. Вместо требования j Î (- p; p] можно взять j Î[- p; p) либо j Î (0, 2p] в зависимости от класса
решаемых задач. |
|
|
||||||||||||||||
Согласно рис.1.1 из п.1.1 |
|
|
||||||||||||||||
x = |
|
z |
|
× cos j, y = |
|
z |
|
× sin j |
|
(1.7) |
||||||||
|
|
|
|
|
||||||||||||||
Но равенство (1.1) справедливо, если вместо ϕ взять |
ϕ + 2kπ, k Z . |
|||||||||||||||||
Множество {j + 2kp |
|
k Î Z} обозначим через Arg z . |
В записи это выглядит |
|||||||||||||||
|
||||||||||||||||||
так: |
|
|
||||||||||||||||
Arg z = {j + 2kp |
|
k Î Z} Û Arg z = j + 2kp, |
k Î Z . |
(1.8) |
||||||||||||||
|
||||||||||||||||||
Имея это в виду, вместо (1.7) можно написать |
|
|
||||||||||||||||
x = |
|
z |
|
× cos Arg z, y = |
|
z |
|
× sin Arg z , |
|
(1.9) |
||||||||
|
|
|
|
|
||||||||||||||
если под Arg z понимать произвольный фиксированный элемент из совокуп-
ности (1.8).
Представление КЧ в виде (1.9) принято называть тригонометрической формой комплексного числа.
Алгебраическая форма КЧ
Множество {(x,0) x Î R} отождествим с множеством действительных
чисел R , полагая
x = (x, 0).
Последнее с геометрической точки зрения вполне объяснимо, так как (x, 0)изображаются точками координатной оси 0x . Но существенным здесь является то, что операция умножения (как и операция суммы) не выводит числа из этого множества. Действительно,
(x1 ,0)× (x 2 ,0) = (x1x 2 - 0 × 0, x1 0 + x 2 0) = (x1x 2 , 0) = x1x 2 ,
тогда как множество {(0, y) y Î R} не отождествляется с R , так как операция
умножения выводит элементы из |
этого |
множества. |
Например, |
(0,1)(0,1) = (0 -1, 0 + 0) = (-1,0) = -1Î R , |
но не |
принадлежит |
исходному |
множеству. Полагая i = (0,1), полученный результат можно записать так:
i 2 = i × i = (0,1)(0,1) = -1 = (- 1,0). |
(1.10) |
ОПРЕДЕЛЕНИЕ 1.3. КЧ i = (0,1) (i 2 = −1) принято называть мнимой
единицей.
Замечание. В этом определении мнимого ничего нет, а речь идет об упорядоченной паре (0,1), для которой выполняется равенство (1.10).
Согласно (1.3) и (1.4)
z = (x, y) = (x,0)+ (0, y ) = (x,0)+ (0,1)(y,0) = x + i y . |
(1.11) |
ОПРЕДЕЛЕНИЕ 1.4. Если КЧ представлено в виде (1.11), то говорят,
что это есть алгебраическая форма КЧ z .
Еще раз обратим внимание читателя на то, что x = Re z, y = Jm z − вещественные числа, а Jm z − коэффициент при мнимой единице.
Замечание. (1.10) и (1.11) позволяют легко перемножать комплексные числа по правилу: умножаем двучлен на двучлен с использованием (1.4) и при-
водим подобные по i . Действительно, z1z 2 = (x1 + i y1 )(x 2 + i y2 ) = x1x 2 +
+ i y1x 2 + i x1 y2 + i 2 y1 y2 = x1x 2 − y1 y2 + i (x1 y2 + x 2 y1 ). Теперь остается сравнить с результатом (1.5) и убедиться в справедливости упомянутого правила.
Перейдем к иллюстративным примерам
ПРИМЕР 1.1. Найти z1z 2 , Re z1z 2 , Jm z1z 2 , если z1 = 1 − 3i , z 2 = −2 + 4 i .
Решение. Согласно только что сформулированному правилу имеем (ум-
ножаем двучлен на двучлен) z1z 2 |
= (1 − 3i)(− 2 + 4 i) = −2 + 6 i + 4 i − 12 i 2 = |
||||||||||||||
= 10 + 10 i, Re z1z 2 |
= 10, Jm z1z 2 |
= 10. |
|
|
|
Ответ: 10 + 10 i, |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Re z1z 2 = 10, Jm z1z 2 = 10. |
||||||
|
|
z 2 |
|
|
|
|
|
|
|
||||||
|
|
1.4 |
|
|
|
|
|
|
ПРИМЕР 1.2. Найти модуль и |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
arg z 2 |
|
аргумент КЧ из ПРИМЕРА 1.1. |
|||||||||
|
|
|
|
|
|
|
|
|
|
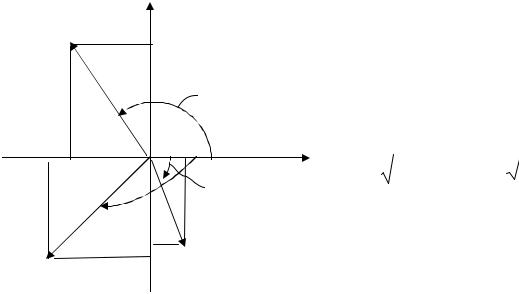
Решение. Построим изображе- |
|||||
|
|
x |
1. |
|
ние z1 |
= (1,−3) (см. рис. 1.2) |
|||||||||
|
|
x |
|
|
|
|
= |
|
= |
|
|
||||
|
|
- - |
|
|
|
|
z1 |
|
12 + (− 3)2 |
|
, |
||||
|
|
|
arg z1 |
|
|
10 |
|||||||||
|
|
|
|
|
arg z1 = −arctg 3, |
||||||||||
|
|
|
|
|
|
||||||||||
|
z |
- |
|
z1 |
|
|
|
Arg z1 = −arctg3 + 2kπ, k Z. |
|||||||
|
|
y |
|
arg z 2 |
= π − arctg 2 , |
||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Arg z 2 |
|
= π − arctg2 + 2kπ = |
|||||||
|
|
Рис. 1.2 |
|
= −arctg2 + (2k + 1)π, k Z. |
|||||||||||
