5. Теорема Куна-Таккера для задачи нелинейной оптимизации. Простейшая интерпретация и способ применения

Теорема Куна-Таккера – основная теорема, дающая возможность решить аналитически задачи нелинейного программирования (оптимизации). Общая математическая формулировка теоремы достаточно сложна. Здесь мы приведем ее упрощенный вариант, позволяющий решать конкретные задачи оптимизации, возникающие в экономике и управлении.

Для задачи нелинейного программирования:

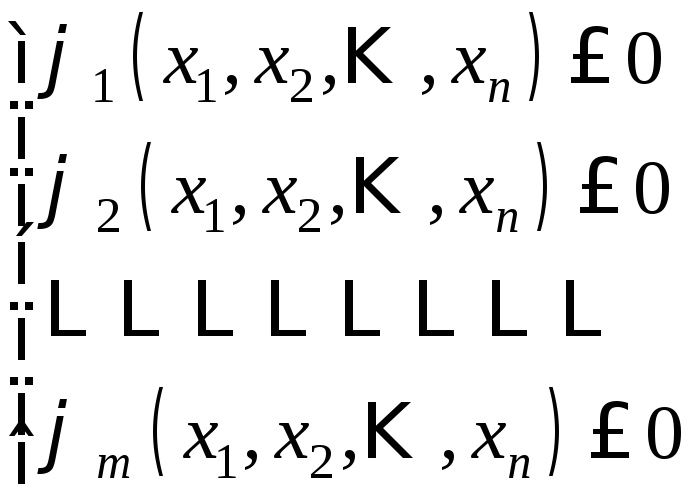(2)

необходимым для точки экстремума является выполнение одного из условий:

1. равенство нулю градиента функции в этой точке;

2. отсутствие градиента функции в точке;

3. равенство нулю хотя бы одного из ограничений (2);

4. бесконечная точка.

Заметим, что равенство нулю ограничений (2) достигается на границе области.

Тогда для отыскания наилучшего значения функции и переменных , при которых оно достигается необходимо выполнить следующийалгоритм поиска глобального экстремума:

1. найти градиент функции;

2. определить все точки, где градиент равен нулю; в тех из них, которые удовлетворяют ограничениям, вычислить значение функции;

3. определить все точки, где градиент не существует; в тех из них, которые удовлетворяют ограничениям, вычислить значение функции (если возможно); для точек разрыва функции определить значения функции при стремлении к точке разрыва со всех сторон;

4. определить максимальные и минимальные значения функции на границах области;

5. исследовать функцию на бесконечности, найти там максимальное и минимальное значение функции;

6. из определенных значений функции во всех потенциально возможных местах экстремума выбрать самое большое (при поиске максимума) или самое маленькое (при поиске минимума); точка, в которой достигается это значение, будет решением задачи оптимизации.

В общем случае проделать эти операции очень непросто. В п.п. 2) и 3) градиент может быть равен нулю или не существовать в бесконечном количестве точек – например на линии или на поверхности в многомерном пространстве. Пункт 4) вообще приводит к самостоятельной задаче поиска условного экстремума. Исследование функции на бесконечности – тоже нетривиальная задача.

Специфика задач экономики и управления заметно упрощает применение этих операций.

Во-первых, в экономических постановках на бесконечности никогда не бывает интересующего нас варианта. Бесконечность или недостижима из-за ограничений, или там реализуется обратный случай. Например, можно достигнуть бесконечных убытков, однако это не представляет интереса. Таким образом, пункт 5) в задачах экономики как правило не исследуется.

Во-вторых, точки, где градиент не существует, в детерминированных экономических постановках бывают известны заранее. Такие точки, соответствующие изломам и разрывам функции, всегда должны иметь экономическое обоснование. Примером могут служить количество товара, при котором начинает действовать скидка, величина дохода, когда меняется ставка налогообложения и т.п. В нашем примере про лесозаготовительный комбинат градиент не существует при количестве рабочих 70 (излом – начинает действовать другая величина затрат на человека) и 150 (разрыв – выплачивается субсидия).

В-третьих, используемые для описания экономических ситуаций функции достаточно просты и имеют, как правило, всего несколько точек, где градиент равен нулю или не имеют таких вообще.