
- •Федеральное агентство по образованию
- •2. Содержание и структура дисциплины (часть 1).
- •Тема 7. Основные теоремы о дифференцируемых функциях и их приложения.
- •Тема 8. Исследование функций с помощью производных, построение их графиков.
- •Раздел III. Функции нескольких переменных.
- •Тема 9. Основные понятия о функции нескольких переменных.
- •Тема 10. Производные и дифференциалы функции нескольких переменных, их приложения.
- •Тема 11. Векторный анализ и элементы теории поля.
- •Дополнительная литература:
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •91. ,,.
- •Раздел II.Дифференциальное исчисление функции одной переменной.
- •Раздел III. Функции нескольких переменных.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта.
- •Часть 1.
- •А); б) ; в) .
- •6.2. Краткие теоретические сведения.
- •Тема 1. Множества. Числовые множества. Функция.
- •Тема 2. Комплексные числа и многочлены.
- •Тема 3. Предел функции. Эквивалентные функции.
- •Тема 4. Числовые последовательности. Предел последовательности.
- •Тема 5. Непрерывность функции.
- •Тема 6. Производные и дифференциалы функции одной переменной.
- •Тема 7. Основные теоремы о дифференцируемых функциях и их приложения.
- •Тема 8. Исследование функций с помощью производных, построение их графиков.
- •7.1 Возрастание, убывание функций. Экстремум.
- •7.2 Наибольшее и наименьшее значения функции.
- •7. 3 Выпуклость, вогнутость, точки перегиба. Асимптоты.
- •7.4 Построение графиков функций.
- •Тема 9. Основные понятия о функции нескольких переменных.
- •Тема 10. Производные и дифференциалы функции нескольких переменных, их приложения.
- •Тема 11. Векторный анализ и элементы теории поля.
- •Тема 12. Неявные и выпуклые функции.
- •Тема 13. Экстремумы функций нескольких переменных.
- •Тема 14. Приложения к общей экономической теории.
- •6.3 Основные математические формулы.
- •С о д е р ж а н и е
Тема 3. Предел функции. Эквивалентные функции.
Число
![]() называетсяпределом
функции
называетсяпределом
функции
![]() при
при
![]() (или в точке
(или в точке
![]() ),
и пишут
),
и пишут![]() ,
если для любого числа
,
если для любого числа![]() найдётся число
найдётся число![]() такое, что при всех
такое, что при всех![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Число
![]() называетсяпределом
функции
называетсяпределом
функции
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если для любого числа
,
если для любого числа![]() найдётся число
найдётся число![]() такое, что при всех
такое, что при всех![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Рассматривают
также односторонние пределы функций:
![]() ,
,![]() ,
,![]() ,
,![]() ,
где
,
где![]() стремится к
стремится к![]() ,
,![]() ,
,![]() или только с левой стороны или только
с правой стороны.
или только с левой стороны или только
с правой стороны.
Основные
утверждения, используемые для вычисления
пределов функций при
![]() (в дальнейшем
(в дальнейшем![]() -
или число
-
или число![]() или символ
или символ![]() ):
):
1)
Если
![]() - постоянная величина, то
- постоянная величина, то![]() .
.
2)
Если существуют конечные пределы
![]() ,
,![]() ,
то:
,
то:
а)
![]() ;б)
;б)
![]() ;
;
в)
![]()
![]() ;г)
;г)
![]() ,
если
,
если![]() .
.
При
вычислении пределов постоянно пользуются
и тем, что для любой основной элементарной
функции
![]() и точки
и точки![]() из её области определения справедливо
соотношение
из её области определения справедливо
соотношение![]() .
.
Функция
![]() называетсябесконечно
большой
при
называетсябесконечно
большой
при
![]() ,
если
,
если![]() .
Функция
.
Функция![]() называетсябесконечно
малой при
называетсябесконечно
малой при
![]() ,
если
,
если![]() .
.
Основные
утверждения для бесконечно больших
функций, используемые для вычисления
пределов при
![]() :
:
1)
Если![]() ,
то
,
то![]() ,если
,если![]() ,
то
,
то![]()
2)
Если
![]() и
и![]() ,
то
,
то![]() .
.
3)
Если
![]() и
и![]() ,
то
,
то![]() .
.
4)
Если
![]() и
и![]() ,
то
,
то![]() .
.
5)
Если
![]() и
и![]() ,
то
,
то![]() .
.
6)
Если
![]() и
и![]() ,
то
,
то![]() .
.
Если
непосредственное применение свойств
конечных пределов и бесконечно больших
функций приводит к неопределённым
выражениям, символически обозначаемым:
![]() ,
то для вычисления предела – «раскрытия
неопределённости» - преобразовывают
выражение так, чтобы получить возможность
его вычислить.
,
то для вычисления предела – «раскрытия
неопределённости» - преобразовывают
выражение так, чтобы получить возможность
его вычислить.
Первым
замечательным пределом
называется предел:
![]() .
Следствиями из него являются пределы:
.
Следствиями из него являются пределы:
![]() ,
,
![]() ,
,![]()
Вторым замечательным пределом называются пределы:
![]()
![]() ,
,
где
![]() -основание
натуральных логарифмов (число Непера).
Он используется для вычисления предела
степенно-показательной функции
-основание
натуральных логарифмов (число Непера).
Он используется для вычисления предела
степенно-показательной функции![]() ,
где
,
где![]() и
и![]() .
.
При
нахождении пределов
![]() следует иметь в виду:
следует иметь в виду:
1)
Если
![]() ,
,![]() ,
то
,
то![]() .
.
2)
Если
![]() ,
,![]() ,
то
,
то![]() вычисляют, учитывая, что:
вычисляют, учитывая, что: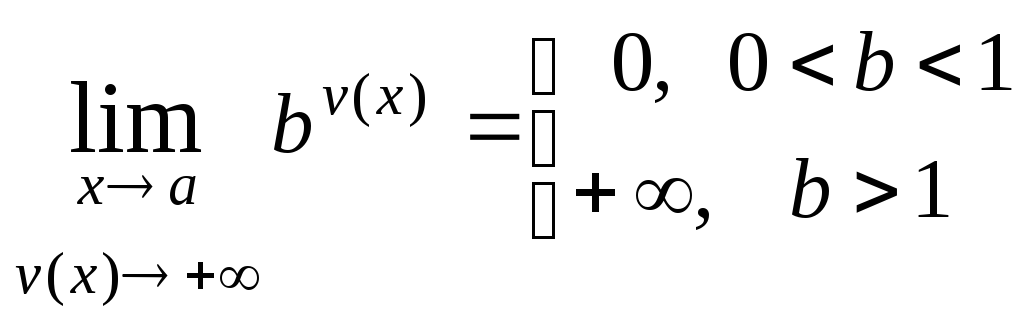 ,
,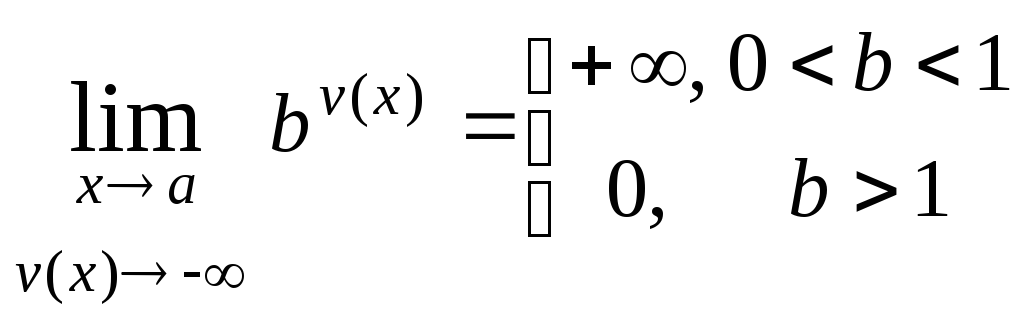 .
.
Бесконечно
малые функции
![]() и
и![]() при
при![]() называютсяэквивалентными,
и пишут
называютсяэквивалентными,
и пишут
![]() ~
~![]() ,
если
,
если![]() .
.
Принцип
замены эквивалентных бесконечно малых
функций, состоит в том, что при вычислении
предела частного
![]() или произведения
или произведения![]() одну из функций (или обе) в этих выражениях
можно заменить эквивалентной функцией.
Так, если
одну из функций (или обе) в этих выражениях
можно заменить эквивалентной функцией.
Так, если![]() ~
~![]() ,
,![]() ~
~![]() при
при![]() ,
то:
,
то:
![]() ;
;
![]()
|
Основные
эквивалентности при
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Тема 4. Числовые последовательности. Предел последовательности.
Если
каждому натуральному числу
![]() по некоторому правилу
по некоторому правилу![]() поставлено в соответствие одно вполне
определённое действительное число
поставлено в соответствие одно вполне
определённое действительное число![]() ,
то говорят, что заданачисловая
последовательность
,
то говорят, что заданачисловая
последовательность
![]() .
Кратко обозначают
.
Кратко обозначают![]() .
Число
.
Число![]() называется
общим
членом последовательности.
Последовательность называют также
функцией натурального аргумента.
Последовательность всегда содержит
бесконечно много элементов, среди
которых могут быть равные.
называется
общим
членом последовательности.
Последовательность называют также
функцией натурального аргумента.
Последовательность всегда содержит
бесконечно много элементов, среди
которых могут быть равные.
Число
![]() называетсяпределом
последовательности
называетсяпределом
последовательности
![]() ,
и пишут
,
и пишут![]() ,
если для любого числа
,
если для любого числа![]() найдётся номер
найдётся номер![]() такой, что при всех
такой, что при всех![]() выполняется неравенство
выполняется неравенство![]() .
.
Последовательность
![]() ,
имеющая конечный предел, называетсясходящейся,
в противном случае – расходящейся.
,
имеющая конечный предел, называетсясходящейся,
в противном случае – расходящейся.
Последовательность
![]() называется:1)
убывающей,
если
называется:1)
убывающей,
если
![]() ;2)
возрастающей,
если
;2)
возрастающей,
если
![]() ;3)
неубывающей,
если
;3)
неубывающей,
если
![]() ;4)
невозрастающей,
если
;4)
невозрастающей,
если
![]() . Все вышеперечисленные последовательности
называютсямонотонными.
. Все вышеперечисленные последовательности
называютсямонотонными.
Последовательность
![]() называетсяограниченной,
если существует число
называетсяограниченной,
если существует число
![]() такое, что для всех
такое, что для всех![]() выполняется условие:
выполняется условие:![]() .
В противном случае последовательность
-неограниченная.
.
В противном случае последовательность
-неограниченная.
Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.
Последовательность
![]() называетсябесконечно
малой,
если
называетсябесконечно
малой,
если
![]() .
Последовательность
.
Последовательность![]() называетсябесконечно
большой
(сходящейся к бесконечности) и пишут
называетсябесконечно
большой
(сходящейся к бесконечности) и пишут
![]() ,
если для любого числа
,
если для любого числа![]() найдётся номер
найдётся номер![]() такой, что при всех
такой, что при всех![]() выполняется неравенство
выполняется неравенство![]() .
.
Числом![]() называется
предел последовательности
называется
предел последовательности![]() ,
где
,
где![]()
Постоянную
![]() называют неперовым числом. Логарифм
числа
называют неперовым числом. Логарифм
числа![]() по основанию
по основанию![]() называется натуральным логарифмом
числа
называется натуральным логарифмом
числа![]() и обозначается
и обозначается![]() .
.
