Методические указания к выполнению контрольных работ

Задача К1. Кинематика точки

Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. Все искомые величины определяются для момента времени t₁, указанного в задании. При решении задачи в некоторых случаях следует учесть известные из тригонометрии формулы:

sin²a + cos²a = 1; sin2a = 2 sina× cosa;

cos2a = 1 – 2sin²a = 2cos²a – 1.

Пример решения задачи К1

Движение точки в плоскости xy задано уравнениями

x=2sin pt/3, y= 2 – cos²pt/3 (x, y – в сантиметрах, t – в секундах).

Определить уравнение траектории точки; для момента времени t₁ = 0,5 с, найти скорость и ускорение точки, а также касательное, нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Р е ш е н и е. 1. Для определения траектории точки исключим из уравнений движения время t. Запишем

y=2 – cos²pt/3 = 2 – (1 – sin²pt/3), (57)

x/2 = sin pt/3. (58)

Подставив уравнение (58) в равенство (57), после преобразований, получим уравнение траектории точки в виде

y = 1 + x²/4, (59)

то есть траекторией точки является парабола, показанная на рис. 14.

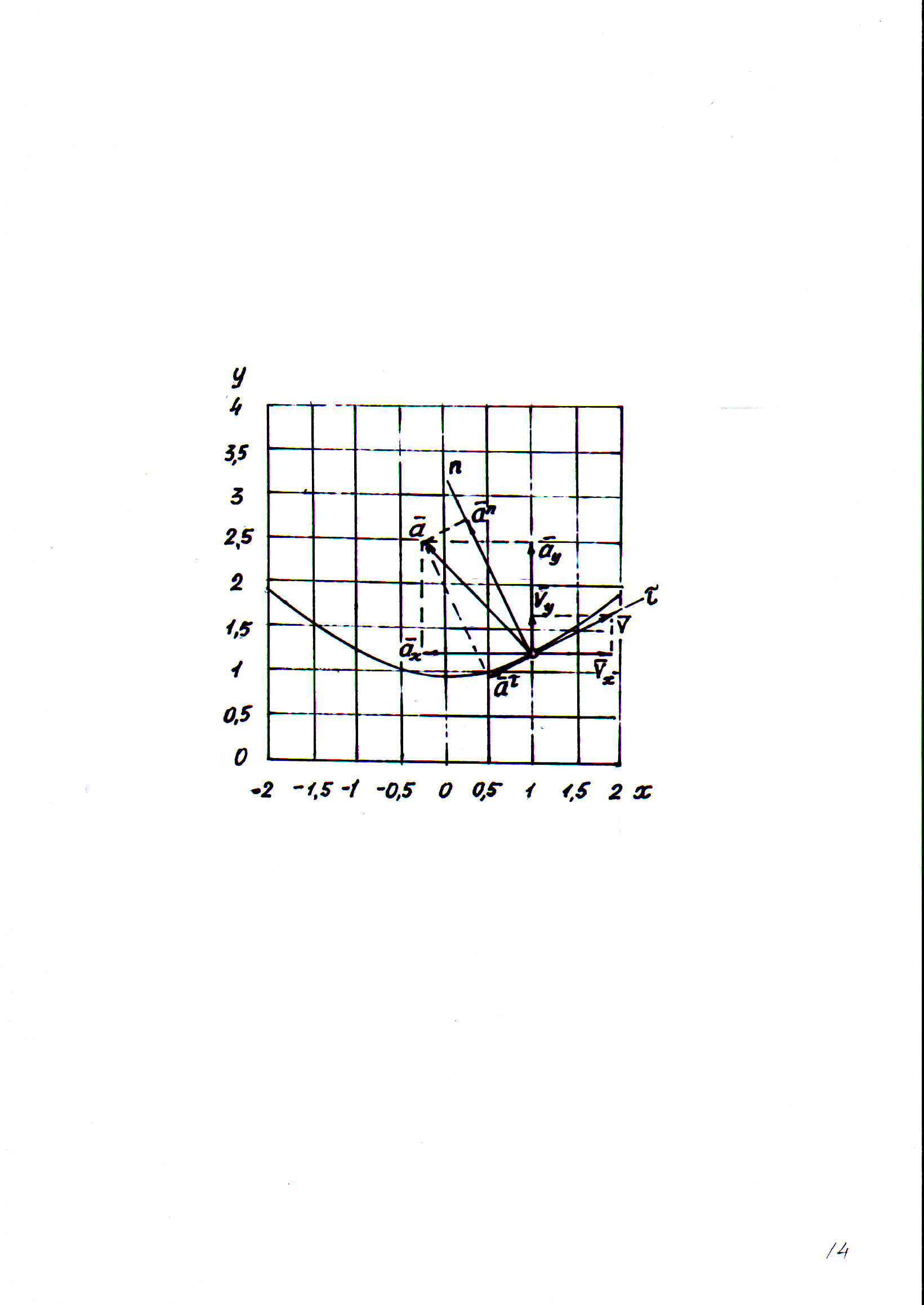
Рис. 14

2. Скорость точки определим по ее проекциям на оси координат:

.

При этом ; .

При t₁ = 0,5 с ν_x = 1,81 см/c, ν_y = 0,906 cм/c, ν = 2,02 см/c.

2. Аналогично определим ускорение точки:

; ; (60)

.

При t₁ = 0,5 с a_x = – 1, 095 см/c², a_y = 1,095 см/c², a = 1,55 см/c².

2. Касательное ускорение

. (61)

2. Нормальное ускорение

. (62)

Подставляя значения величин, входящих в уравнения (61) и (62) при t₁ = 0,5 c, получим числовые значения

a_t = 0,49 см/c², a_n = 1,47 см/c².

2. Радиус кривизны траектории

.

Подставляя численные значения v и a_n при t₁ = 0,5 c, получим значение r = 2,8 см.

На рис. 14 показано положение точки в заданный момент времени, т. е. при t₁ = 0,5 c с координатами x = 1 см, y = 1,25 см. Здесь же показаны векторы скорости и ускоренияи их составляющие.

О т в е т: v = 2,02 см/c; a = 1,55 см/c²; a_t = 0,49 см/c²; a_n = 1,47 см/c²; r = 2,8 см.

Задача К2. Кинематика простейших движений твердого тела

Задача К2 является комбинированной. Она охватывает вопросы кинематики точки, поступательного, вращательного и плоского движения твердого тела. Приступая к решению задачи, необходимо изучить теоретический материал, примеры и задачи по темам, указанным выше. Особо обратить внимание на естественный способ задания движения точки и определение ее скорости в этом способе; на способы определения положения мгновенного центра скоростей при плоском движении тела и применение его для определения скоростей других точек этого тела; на применение теоремы о проекциях скоростей двух точек тела на прямую, их соединяющую. Кроме того, следует при решении задач обратить внимание на то, что скорости контактирующих точек тел будут равны (считаем, что проскальзывание отсутствует). Порядок расчета приводится в примере.

Пример решения задачи К2

Схема механизма приведена на рис. 15.

Исходные данные: r₁ = 0,5 м; r₂ = 0,3 м; r₃ = 0,6 м; L₁ = 0,4 м; L₂ = 1,0 м; CM = 0,2 м; φ = 30 ^o; β = 90 ^o.

Требуется определить в заданном положении механизма:

1. Угловые скорости колес ω₁ и ω₂;

2. Уравнения вращения кривошипа φ = f(t) и время t₁, соответствующее заданному положению кривошипа;

3. Скорость ν_B и ускорение а_B точки В колеса;

4. Скорость и ускорение точек D и M шатуна;

5. Угловую скорость ω_DC и угловое ускорение шатуна.

Закон движения точки А рукоятки: S = (π / 3) t ².

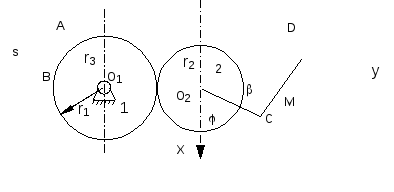
Рис. 15

Р е ш е н и е.

1. Рукоятка О₁А жестко связана с колесом 1, поэтому ее угловая скорость равна ω₁, а линейная скорость точки А равна 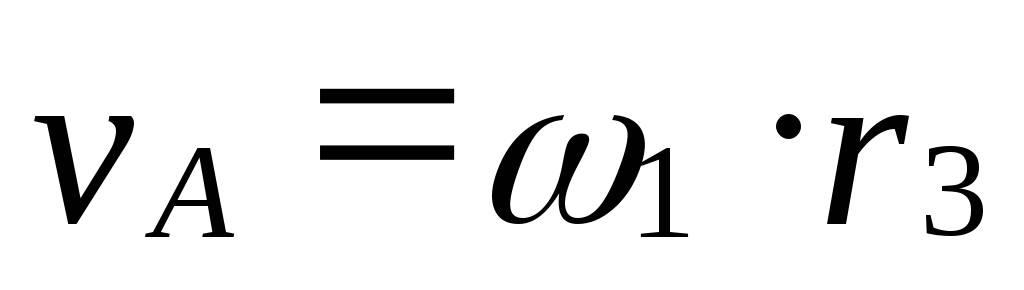, откуда (рис. 16)

. (63)

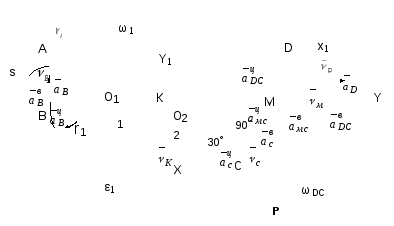
Рис. 16

С другой стороны, уравнение движения точки А задано естественным способом:

, (64)

поэтому скорость точки А

. (65)

Из (63) и (65) находим

. (66)

Для определения ω₂ запишем выражение скорости точки касания колес К (рис. 16), рассматривая ее принадлежащей каждому из колес:

, .

Приравнивая скорости, находим

(67)

или с учетом (66)

. (68)

Так как время движения механизма в заданное положение нам пока неизвестно, то, подставив значения радиусов, получим выражение угловых скоростей в общем виде. С учетом общепринятого правила знаков, вращение против хода часовой стрелки считается положительным:

; . (69)

Найдем уравнение движения кривошипа. Учитывая, что он жестко связан с колесом 2, запишем:

,

откуда находим

. (70)

Постоянную С₁ определяем по начальным условиям: при t = 0 кривошип совпадал с направлением оси Х, поэтому φ₀ = 0. Подставляя в (70), получим С₁ = 0, и уравнение вращения кривошипа имеет вид

φ = 0,915πt² . (71)

Определим t₁ – время движения механизма в заданное положение, положив значение угла φ равным заданному, т. е. φ = 30^o или φ = π/6. Из уравнения (8) находим, что t₁ = 0,43 с, т. к. время считается положительным. Подставляя t₁ в (69), получим значения угловых скоростей в заданном положении:

ω₁ = –1,48 рад/с; ω₂ = 2,47 рад/с.

Направление вращения колес показано стрелками на рис. 16.

2. Определим скорость и ускорение точки В колеса 1. По модулю скорость точки В колеса определяется выражением

. (72)

В момент времени t = t₁ получим = 0,74 м /с.

Вектор скорости направлен в сторону вращения колеса перпендикулярно радиусу (рис. 16).

Ускорение точки В равно векторной сумме вращательного и центростремительного ускорений

.

Величины вращательной и центростремительной составляющих вектора вычисляются по формулам

, . (73)

3. Угловое ускорение 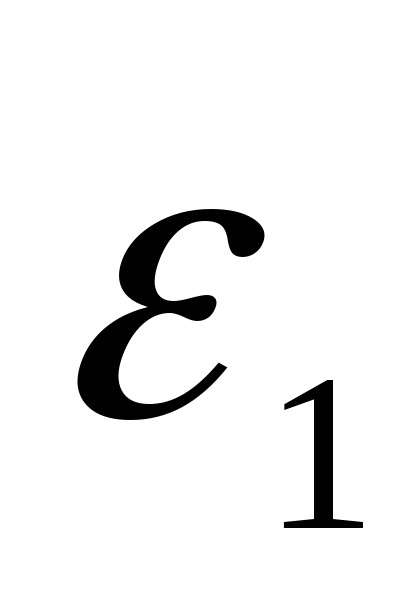определим, дифференцируя по времени первое выражение в (69):

.

Т. к. знаки ω₁ и совпадают, то вращение колеса будет ускоренным и направление вращательной составляющей ускорениясовпадает с направлением скоростиν_B. Центростремительная составляющая ускорения всегда направлена к оси вращения (рис. 16).

Подставляя в (73) численные значения ,ω₁, r₁ находим

, .

Тогда модуль полного ускорения

.

4. Переходим к определению скорости и ускорения точек D и M шатуна DC.

а) Определение скорости точек D и М.

Для определения скорости точки D воспользуемся теоремой о равенстве проекций скоростей двух точек плоской фигуры на прямую, соединяющую точки. Действительно, направление скоростей точек D и С шатуна известны, кроме того, может быть найден и модуль скорости точки С. Если рассматривать точку С как точку, принадлежащую кривошипу О₂С, жестко связанному с колесом 2, то по модулю величина

= ω₂ O₂C

или для t = t₁

= 2,47× 0,4 » 0,99 (м/с).

Так как вектор скорости направлен перпендикулярно кривошипу О₂С в сторону его поворота, то вектор направлен вдоль шатуна СD. Вектор скороститочки D направлен вдоль направляющих ползуна (рис. 16). Проецируя векторы скоростей на прямую CD, получим:

= × cos30^o.

Отсюда находим

= / cos30^o =1,14 м/с.

Скорость точки М определим с помощью мгновенного центра скоростей. Если за полюс в теореме о сложении скоростей принять мгновенный центр скоростей, то скорость любой точки плоской фигуры можно рассматривать как вращательную при мгновенном повороте плоской фигуры вокруг мгновенного центра скоростей. Положение мгновенного центра скоростей определим как точку Р пересечения перпендикуляров, проведенных в точках С и D к направлению скоростей этих точек. Запишем выражения, определяющие модули скоростей точек D и M

= ω_DC ×PD, =ω_DC× PM . (74)

Из первого равенства найдем угловую скорость ω_DC шатуна при t = t₁

ω_DC = / PD = 1,14 / 2 =0,57 рад/с,

а из второго – скорость точки М

.

Скорость направлена по нормали к прямой МР в сторону поворота шатуна CD.

б) Определение ускорений точек D и М.

Выберем за полюс точку С, ускорение которой можно определить. Согласно теореме сложения ускорений, ускорение любой точки плоской фигуры, например точки D, теперь определится по формуле

, (75)

где а_С – ускорение полюса;

–ускорение точки D во вращательном движении плоской фигуры вокруг полюса.

Модули составляющих ускорения а_DС вычисляются по формулам:

, . (76)

Ускорение полюса С, если рассматривать его как точку, принадлежащую кривошипу, совершающего вращательное движение, также определяется двумя составляющими

, (77)

модули которых равны

, . (78)

Величину найдем, дифференцируя по времени выражениеω₂ в (69)

.

Так как знаки ω₂ и совпадают, то вращение второго колеса, а следовательно, и кривошипа, ускоренное, т. е. направление векторабудет совпадать с направлением вектораν_C. Вектор направлен к оси вращения кривошипа. Подставляя в (78) числовые значения приt = t₁ получим

, .

В уравнениях (76) можно определить только величину , так какпока неизвестно. Подставляя числовые значенияω_DC и L₂, получим

.

Вектор направлен от точки D к полюсу С. Таким образом, в уравнение (75) входят две неизвестные по модулю величиныи; линии, по которым эти векторы направлены, известны. Зададим направление этих векторов, как указано на рис. 16. Теперь спроецируем уравнение (75) на выбранные направления координатных осей Х иY, получим два уравнения, в которые войдут два неизвестных. Проецируя на ось Х, получим

, (79)

на ось Y

. (80)

Из уравнения (79) находим , из уравнения (80). Так как знаки положительны, то направления векторовиа_D выбраны правильно.

Теперь из формулы (76) найдем угловое ускорение и запишем для определения ускорения точки М формулу

. (81)

Модули составляющих иопределены по формулам, аналогичным (76):

,

.

Введем оси Х₁ и Y₁, направленные вдоль шатуна и перпендикулярно ему, и спроецируем на них уравнение (81):

на Х₁: ,

на Y₁: .

Модуль ускорения точки М равен

.

в) Аналитический метод определения скорости и ускорения точки тела при плоском движении (рис. 16).

Приведем пример аналитического метода расчета скорости и ускорения точки М.

Запишем радиус-вектор точки М: .

Проецируя эту формулу на оси координат, обозначив угол между осью X и прямой СD через γ, получим координаты точки М:

; .

Взяв производные по времени, найдем проекции вектора скорости точки М на оси координат

; .

Здесь – угловые скорости звеньев О₂С и CD. Взяв производные по времени от проекций вектора скорости, получим проекции на оси координат вектора ускорения:

;

.

Здесь – угловые ускорения звеньев О₂С и CD.

Используя эти проекции, можно найти скорость и ускорение точки М:

. Запишем координату_:

=const.

Дифференцируя по времени это выражение, получим

.

Определим угловые скорости и угловые ускорения звеньев О₂С и СD, для чего

.

Отсюда находим

.

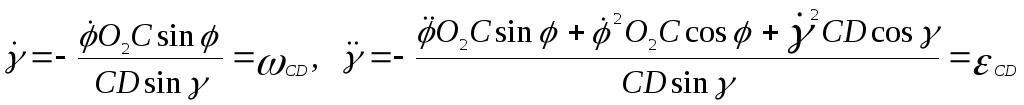Подставляя для заданного положения механизма:

, О₂С = 0,4 м, CD = 1 м, ,получаем .

Находим при СМ = 0,2 м,

.

Задача К3. Сложное движение точки

По заданному уравнению вращения φ = f₁(t) тела А и уравнению движения S = OM = f₂(t) точки М относительно тела А определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = t₁. Точка М на рисунках 17 и 18 показана в направлении положительного отсчета координаты S. Положительное направление отсчета угла φ указано стрелкой.

Пример решения задачи К3

При решении задачи К3 необходимо определить, какое движение точки будет относительным, а какое переносным. Скорость и ускорение точки в относительном движении в этой задаче определяются методами кинематики точки, а в переносном – кинематики твердого тела.

Схема к задаче приведена на рис. 17.

Исходные данные: уравнение вращения тела А задано в виде φ = 4t – 5t³, а уравнение движения точки М относительно тела А

S = 12sin см;

R = см.

Определить абсолютную скорость и абсолютное ускорение точки М при t = t₁ = 1 с.

Р е ш е н и е.

Точка М совершает сложное движение. Относительным движением точки М является движение относительно тела А, переносным – вращение тела А вокруг оси ВС. Свяжем с телом А подвижную систему координат, направив ось Х перпендикулярно плоскости рисунка на нас (рис. 18).

Положение точки М в момент времени t = t₁ = 1 с определим углом α, на который повернется радиус, проведенный из центра О₁ в точку М, за время движения.

= =.

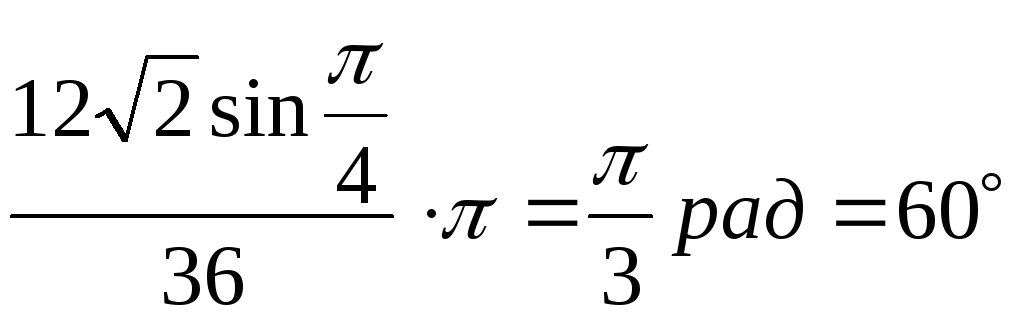Абсолютная скорость точки М равна геометрической сумме относительной и переносной скоростей:

. (82)

Движение точки М относительно тела А задано естественным способом, поэтому относительную скорость определяем из формулы

,

при t₁=1 c = 3= 9,4 см/с.

Так как знак скорости положителен, то вектор направлен в сторону возрастания координатыS (положительное направление отсчета) по касательной к траектории, т. е. перпендикулярно радиусу R в точке М.

Переносная скорость точки М равна скорости той точки тела А, с которой она совпадает в данный момент. Тело А совершает вращательное движение вокруг оси ВС, поэтому по модулю

= ω MK,

где МK – расстояние от точки М до оси ВС;

ω – угловая скорость переносного вращательного движения.

Так как уравнение вращательного движения φ = f₁(t) задано, то находим

,

при t₁=1 c ω = 4 – 15 ^. 1² = –11 рад/с.

Знак минус указывает на то, что в момент времени t₁=1 c тело А вращается в направлении, противоположном положительному отсчету угла φ (рис. 18).

При t₁=1 с расстояние МK равно

МK = R – R cos 60^o = 0,5 R = 5,7 см.

Величина переносной скорости при t₁=1 c

= 11 ^. 5,7 = 62,7 см/с.

Вектор направлен перпендикулярно МК в сторону вращения тела, т. е. параллельно оси Х от нас. Так как в данном случае векторы и взаимно перпендикулярны, то модуль абсолютной скорости точки М

,

при t₁=1 c

Переходим к определению абсолютного ускорения точки М.

Согласно теореме сложения ускорений (теорема Кориолиса) абсолютное ускорение точки в случае переносного вращательного движения равно геометрической сумме относительного, переносного и кориолисова ускорений

. (83)

При естественном способе задания относительного движения относительное ускорение точки определяется выражением

.

Величины касательной и нормальнойсоставляющих равны:

,

.

При t₁ = 1 с, ,.

Так как знаки величин иразличны, то относительное движение является замедленным и векторпротивоположен вектору. Векторнаправлен к центру кривизны траектории в относительном движении, т. е. по радиусу к точке О₁ (рис. 18).

Переносное ускорение точки М также складывается из двух составляющих:

,

т. к. переносное движение является вращательным. По модулю вращательная составляющая и центростремительная составляющаяпереносного ускорения определяются выражениями

, , (84)

где – угловое ускорение тела А.

По определению

.

При t₁ = 1 с

Знаки исовпадают, поэтому совпадают направления векторови, а такжеи. Векторнаправлен к оси вращения, т. е. по линии МK к точке K (рис. 18). Подставляя в (84) численные значения входящих величин, при t₁ = 1с имеем

,

Вектор кориолисова ускорения определяется по формуле

. (85)

Его модуль

.

Из рис. 18 видно, что угол между векторами иравен = 60^о, поэтому при t₁ = 1 с

.

В соответствии с правилом векторного умножения вектор направлен перпендикулярно плоскости рисунка от нас, т. е. совпадает с направлением(рис. 18). Перепишем уравнение (83) в виде

(86)

и определим модуль абсолютного ускорения точки М, используя способ проекций. Проецируя уравнение (86) на оси координат OXYZ, находим

.

Отсюда находим