1. Кинематика точки

Непрерывную кривую, которую описывает точка при своем движении в пространстве, называют траекторией точки. Если траектория – кривая линия, то движение точки называется криволинейным, частным случаем которого является движение точки по прямой линии, то есть прямолинейное движение. В дальнейшем будет рассматриваться общий случай движения точки.

Исходя из того, что основными пространственно-временными (кинематическими) характеристиками движения точки являются ее положение, скорость и ускорение, то задачами кинематики являются:

- нахождение способа задания движения точки;

- исходя из этих способов разработка методов определения ее траектории, скорости и ускорения.

Движение точки по отношению к выбранной системе отсчета считается заданным, если известен способ, позволяющий определить положение точки в любой момент времени. Следовательно, задать движение точки – это значит указать способ, позволяющий в любой момент времени определить ее положение по отношению к выбранной системе отсчета. Известны три способа задания движения точки: векторный; координатный; естественный.

1.1. Векторный способ задания движения

Проведем из некоторой точки тела отсчета (рис. 1) в движущуюся точку М радиус-вектор . Тогда положение точки М будет вполне определено, если ее радиус-вектор известен как функция времени t. Зависимость

(1)

называется законом (уравнением) движения точки в векторной форме.

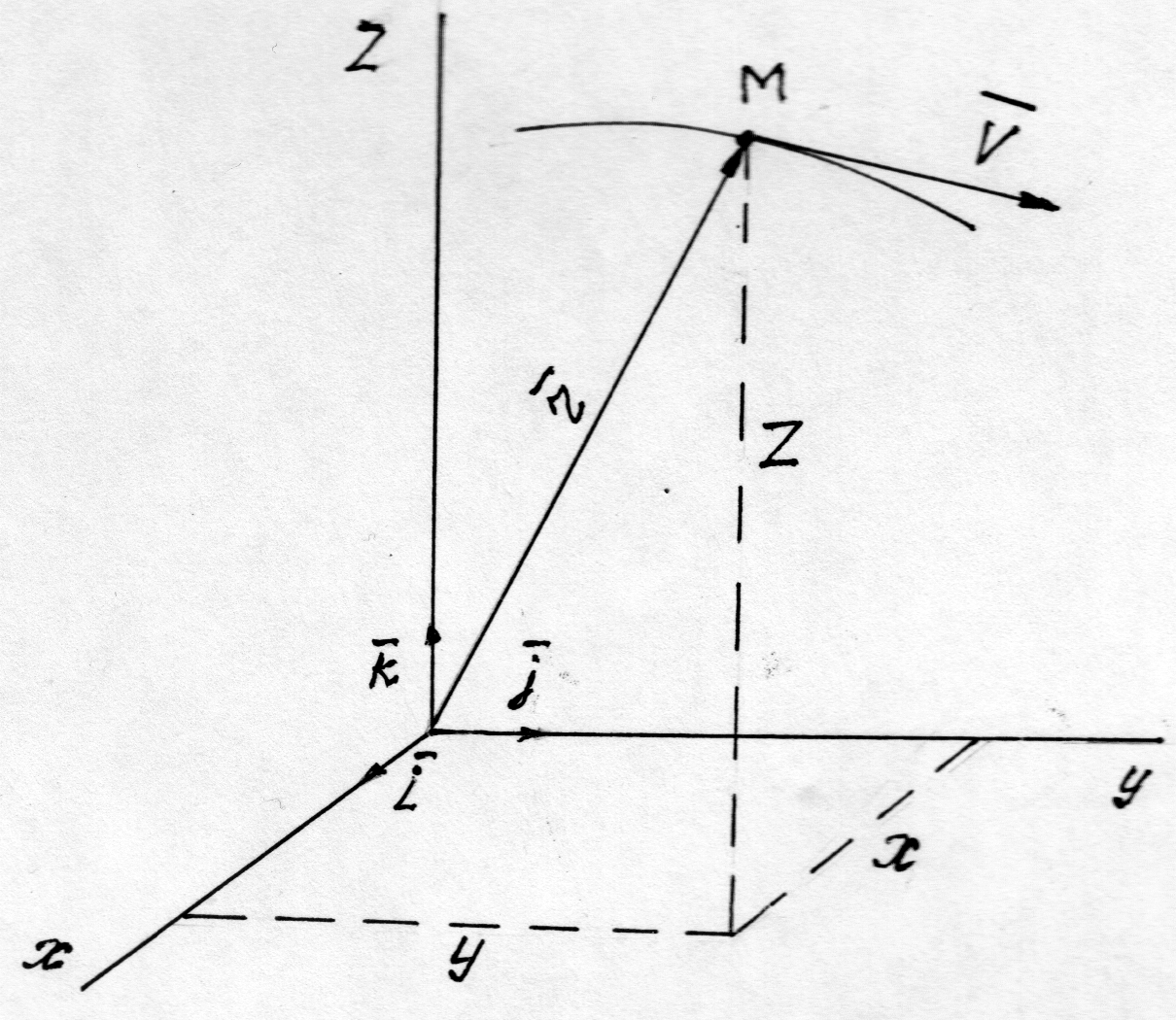
Рис. 1

Скорость точки в данный момент времени, которую обозначим , равна первой производной по времени от ее радиуса-вектора

, (2)

а вектор скорости направлен по касательной к траектории в данной точке.

Ускорение точки, которое обозначим , характеризует быстроту изменения вектора скорости по модулю и направлению, тоже является векторной величиной и равно первой производной по времени от вектора скорости точки или второй производной по времени от ее радиуса-вектора

. (3)

Вектор ускорения точки лежит в соприкасающейся плоскости и направлен в сторону вогнутости ее траектории.

1.2. КООРДИНАТНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ

Свяжем с телом отсчета некоторую систему координат. Наиболее часто используют прямоугольную декартову систему координат, в которой положение точки задается ее линейными параметрами – координатами x, y ,z (рис. 1). Способ задания движения, заключающийся в задании координат точки как известной функции времени t, называется координатным способом задания движения. Зависимость координат от времени, то есть

x = f (t), y = y(t), z = z(t) (4)

называется уравнениями или законом движения точки в координатной форме. Из уравнений (4) можно получить уравнение траектории точки, если исключить из них время.

При этом способе задания движения модуль скорости точки определяется через ее проекции на оси декартовых координат в виде

. (5)

Здесь проекции вектора скорости на оси координат определяются как первые производные по времени от соответствующих координат, то есть по формулам:

. (6)

Направление вектора скорости задается направляющими косинусами:

. (7)

Аналогично определяется и модуль ускорения точки:

, (8)

где проекции ускорения точки на оси координат определяются первыми производными по времени от соответствующих проекций скорости или вторыми производными по времени от соответствующих координат:

. (9)

Направление вектора ускорения также определяется направляющими косинусами

. (10)

1.3. естественный способ задания движения

Этот способ применяют, когда траектория точки известна. Траекторию точки выбирают за криволинейную ось s, отметив на ней неподвижную точку О, которую принимают за начало отсчета, а также положительное и отрицательное направление отсчета (рис. 2). Положение движущейся точки М на траектории однозначно определяется криволинейной координатой s, равной длине дуги ОМ, взятой с соответствующим знаком.

Зависимость координаты s от времени t, то есть

s=s(t), (11)

называется уравнением или законом движения точки М в естественной форме. В случае прямолинейного движения точки вдоль оси Ox, координата s = x и законом прямолинейного движения будет

x= f(t). (12)

Алгебраическая величина скорости точки в данный момент времени равна первой производной от координаты s по времени t:

. (13)

Направлен вектор скорости по касательной к траектории. Если знак v положителен, то вектор направлен в положительном направлении отсчета координатыs, в противном случае – в противоположном.

Ускорение точки при естественном способе задания движения определяют по его проекциям на ортогональные естественные оси координат , имеющие начало в точке М и движущиеся вмести с нею (рис. 2).

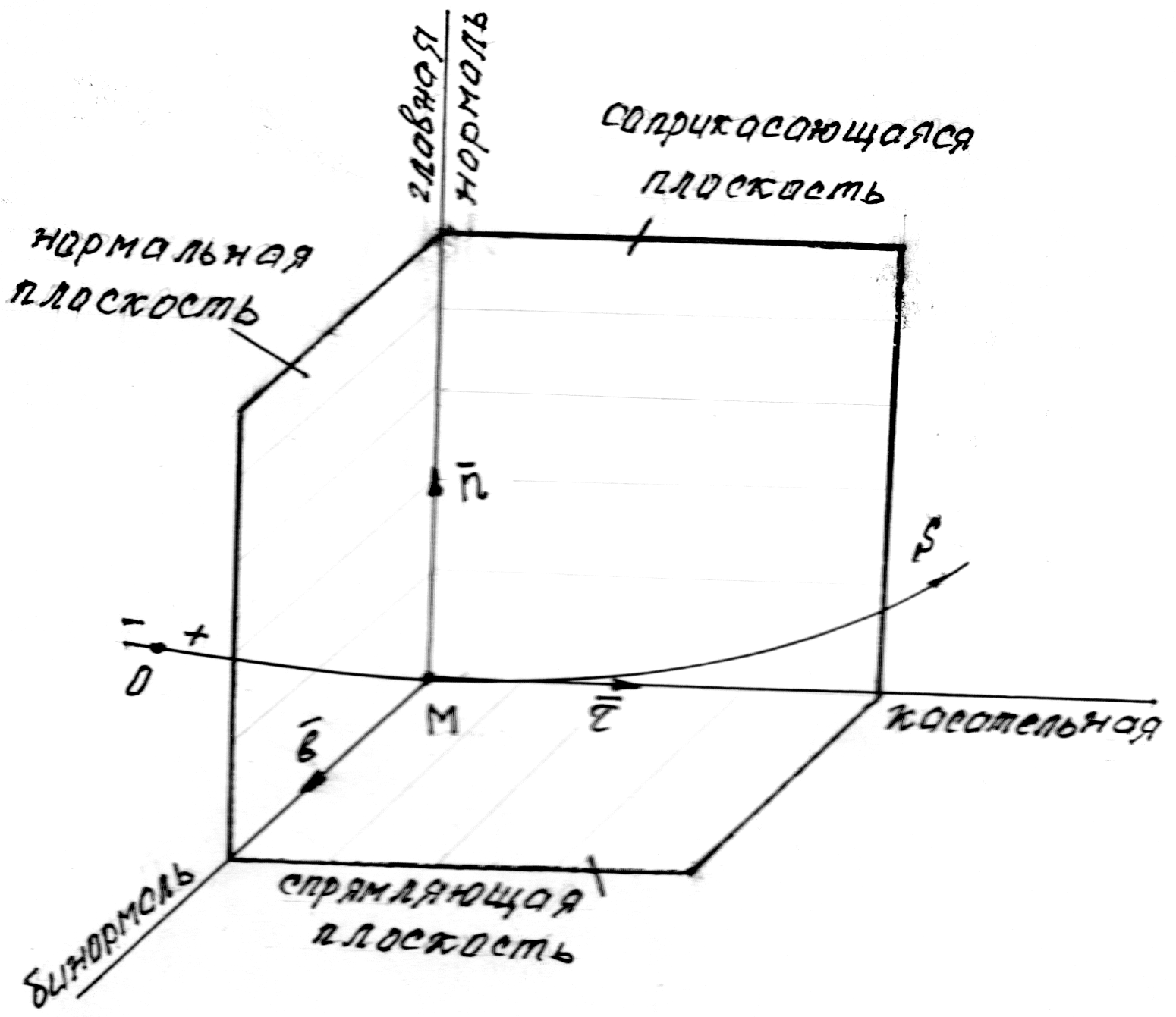
Рис. 2

Ось M направлена вдоль касательной к траектории в сторону положительного отсчета координаты s и называется касательной осью; ось Mn – по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось Mb перпендикулярна двум первым и образует с ними правую систему координат. Ось Mn называется главной нормалью, ось Mb называется бинормалью; – единичные векторы соответствующих осей.

Так как ускорение лежит в соприкасающейся плоскости, то проекция вектора ускорения на бинормаль равна нулю, т. е. а_b = 0. Проекция вектора ускорения на касательную ось равна первой производной по времени от алгебраического значения скорости или второй производной по времени от дуговой координаты:

. (14)

Это ускорение называют касательным или тангенциальным ускорением.

Вектор касательного ускорения . Еслиположительно, то векторсовпадает с направлением вектора, т. е. направлен в сторону возрастания дуговой координатыs.

Проекция вектора ускорения на главную нормаль называется нормальным ускорением и определяется выражением

, (15)

где  – радиус кривизны траектории в данной точке кривой. Если траектория – окружность радиуса R, то  = R; если траектория – прямая линия, то  равно бесконечности. Вектор нормального ускорения всегда направлен в сторону вогнутости траектории. Ускорение точки равно и изображается диагональю параллелограмма, построенного на составляющихи. Так как эти составляющие взаимно перпендикулярны, то модуль ускорения определяется формулой

. (16)