2. Кинематика простейших движений твердого тела

В теоретической механике тела считают абсолютно твердыми, то есть расстояния между точками тела остаются во время движения неизменными.

Основными задачами кинематики твердого тела являются:

1. Задание движения и изучение кинематических характеристик движения всего тела в целом.

2. Изучение движения каждой из точек тела в отдельности.

2.1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ

Движение тела называют поступательным, если любая прямая, проведенная в нем, остается во все время его движения параллельной самой себе.

При этом виде движения все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Пусть точки А и В принадлежат телу, совершающему поступательное движение. Тогда

, .

Таким образом, для задания поступательного движения тела достаточно задать движение одной его точки. Это можно сделать одним из методов кинематики точки.

2.2. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ

Движение тела называют вращательным, если две его (или неизменно с ним связанные) точки остаются во все время движения неподвижными.

Прямая, проходящая через эти неподвижные точки, называется осью вращения. Все точки оси вращения также неподвижны. Остальные точки тела описывают траектории в виде окружностей с центрами на оси вращения в перпендикулярных ей плоскостях.

Положение тела можно задать углом  между некоторой неподвижной полуплоскостью и подвижной, жестко связанной с телом, проведенными через ось вращения. Этот угол называют углом поворота тела и измеряют в радианах. Зависимость угла поворота тела от времени, т. е. зависимость

=f(t) (17)

называется уравнением или законом вращательного движения тела. Выберем положительное направление оси вращения, тогда угол поворота считается положительным, если при наблюдении с положительного направления оси вращения, поворот тела представляется происходящим против хода часовой стрелки.

Основными кинематическими характеристиками вращательного движения тела являются его угловая скорость  и угловое ускорение .

Угловая скорость тела в данный момент времени равна первой производной по времени от угла поворота

(18)

и имеет размерность рад/сек. Угловую скорость удобно представить в виде вектора , который направлен по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки и равный по модулю угловой скорости (рис. 3,а). Тогда при  > 0 вращение тела совпадает с направлением положительного отсчета угла .

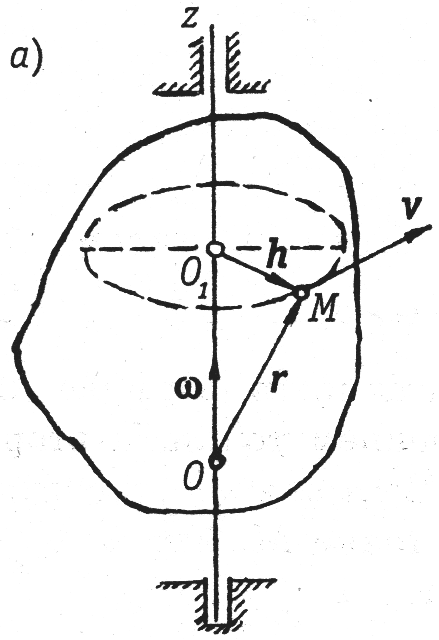
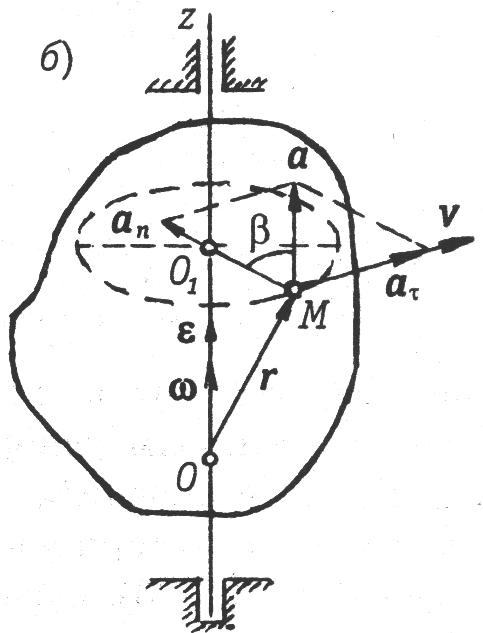
Рис. 3

В технике угловую скорость часто определяют числом оборотов в минуту (n об/мин). Связь между этими единицами измерения дается формулой

. (18 а)

Угловое ускорение тела ε в данный момент времени равно первой производной по времени от угловой скорости или второй производной по времени от угла поворота,

(19)

и измеряется в рад/сек². Если знаки  и  одинаковы, то вращение тела ускоренное, в противном случае – замедленное. Угловое ускорение тела можно также изобразить в виде вектора , направленного по оси вращения и совпадающего с направлением вектора , если вращение тела ускоренное (рис. 3, б), и противоположно направленного, если замедленное.

В случае равномерного вращения, то есть когда угловая скорость ω постоянна, закон вращательного движения имеет вид:

, (20)

где – начальный угол отсчета угла поворота.

При равнопеременном вращении, то есть когда постоянно угловое ускорение ε, угловая скорость ω и угол поворота φ (закон движения) определяются формулами

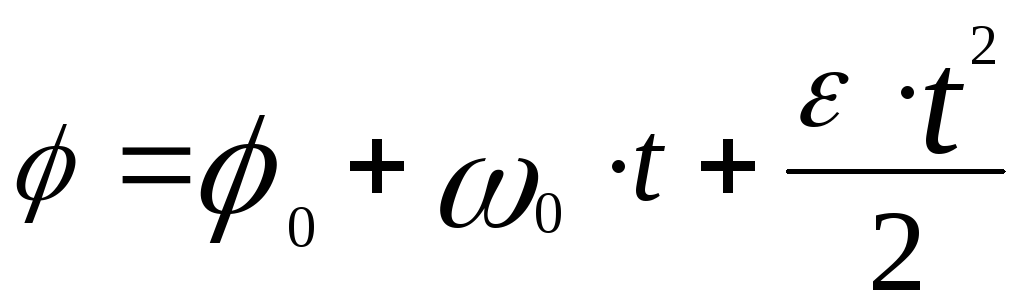, , (21)

где – угловая скорость и угол поворота в момент времени начала отсчета (начальные условия). Обычно момент времени начала отсчета принимают равным нулю.

Скорость и ускорение точки тела при вращательном движении определяют исходя из естественного способа задания движения, используя кинематические характеристики вращательного движения. Так как длина дуги окружности равна , гдеh – расстояние от точки до оси вращения (радиус окружности), то из формулы (13) следует:

,

или

. (20)

Вектор скорости перпендикулярен радиусу окружности, которую описывает точка при своем движении, и направлен в сторону вращения тела (рис. 3, а).

Ускорение точки определим через его составляющие, применяя формулы (14), (15), (16):

а) составляющая

, (21)

касательное или тангенциальное ускорение (вектор этого ускорения совпадает по направлению с направлением вектора скорости, если знаки угловой скорости и углового ускорения одинаковы);

б) составляющая

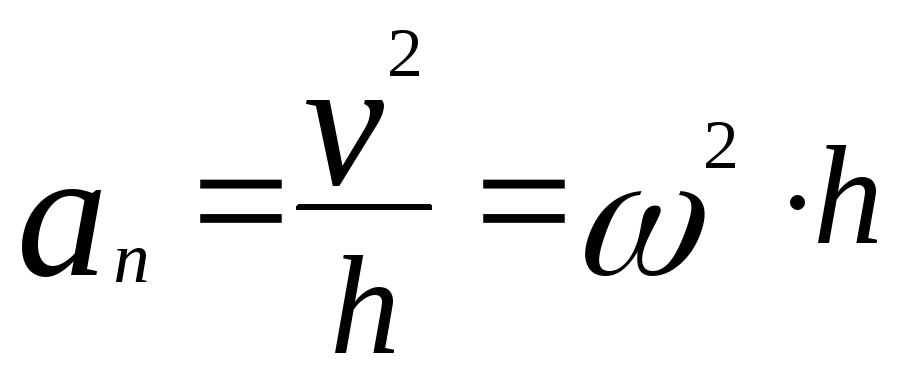, (22)

нормальное или центростремительное ускорение (направлено по радиусу к оси вращения).

Полное ускорение точки определяется по модулю выражением (рис. 3, б):

. (23)

Скорость точки можно записать в векторной форме, которую называют формулой Эйлера

, (24)

где – радиус-вектор точки, проведенный из любой точки на оси вращения. Эта формула определяет скорость точки тела как по модулю, так и по направлению. Используя эту формулу, можно получить векторные формулы для определения составляющих ускорения точки тела:

а) касательное, или тангенциальное ускорение

; (25)

б) нормальное, или центростремительное ускорение

. (26)

В векторной форме полное ускорение точки записывают в виде:

. (27)

2.3. Плоское (плоскопараллельное) движение тела

Движение тела называют плоским, если все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Так как любая прямая, проведенная в теле перпендикулярно неподвижной плоскости движется поступательно, то есть все ее точки движутся одинаково, то для изучения движения тела достаточно изучить движение плоской фигуры, полученной от пересечения тела любой плоскостью Q, параллельной неподвижной плоскости.

Закон плоского движения записывают как зависимость от времени t координат некоторой его точки, называемой полюсом, например точки А, т. е. и угла поворота вокруг полюса, который отсчитывают от направления некоторой прямой АВ, проведенной в сечении плоской фигуры и одной из координатных осей, например с осьюx. Уравнения

, (28)

позволяют найти закон движения произвольной точки сечения плоской фигуры (рис. 4).

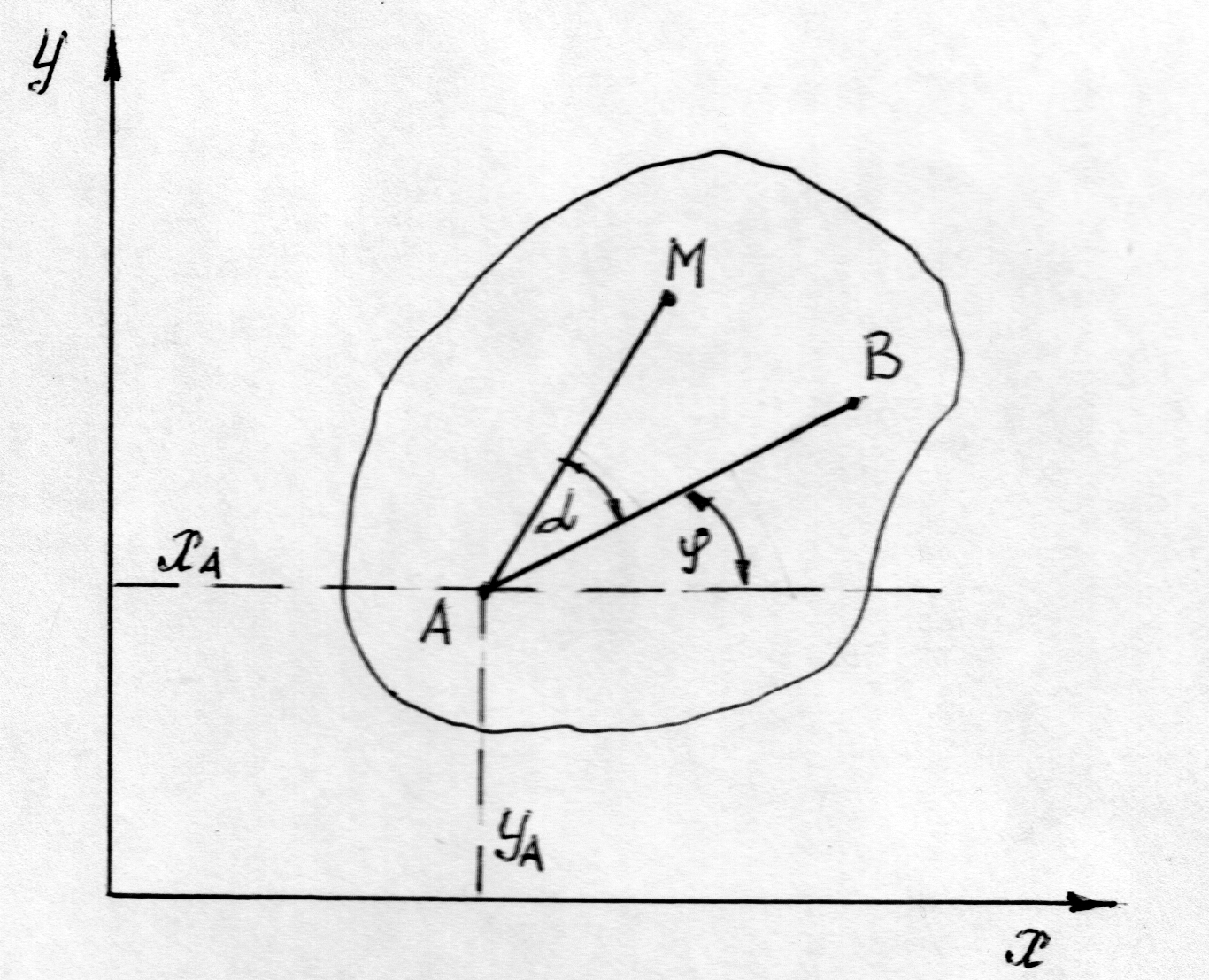
Рис. 4

Пусть длина отрезка АВ = b, тогда закон движения точки В запишется в виде

, . (29)

Для произвольной точки М плоской фигуры, у которой прямая АМ = d составляет с прямой АВ угол α, закон движения этой точки запишется в виде

. (30)

Так как угол α величина постоянная, то здесь только те же три величины зависят от времени.

Плоское движение можно рассматривать как совокупность поступательного движения вместе с полюсом и вращательного вокруг полюса. Необходимо отметить, что поступательная часть движения зависит от выбора полюса, а вращательная часть не зависит, то есть вращение вокруг любого полюса происходит с одним и тем же значением угловой скорости ω и углового ускорения ε. Векторы угловой скорости и углового ускорения считают направленными перпендикулярно к плоскости движения.

Определение скорости точки при плоском движении тела

За полюс выбирают точку, у которой линейные скорость и ускорение известны либо могут быть определены по данным задачи. В векторной форме выражение скорости произвольной точки В имеет вид:

, (31)

где – скорость полюса,скорость точки В при вращении тела вокруг полюса А.

В векторной форме эта скорость определяется формулой

. (32)

По модулю эта скорость равна

(33)

и направлена перпендикулярно отрезку АВ в сторону поворота тела.

Таким образом, выражение скорости точки может быть записано в виде

. (34)

Формула (34) выражает теорему о распределении скоростей: «Скорость точки плоской фигуры складывается из скорости точки, принятой за полюс, и скорости при вращательном движении вокруг полюса».

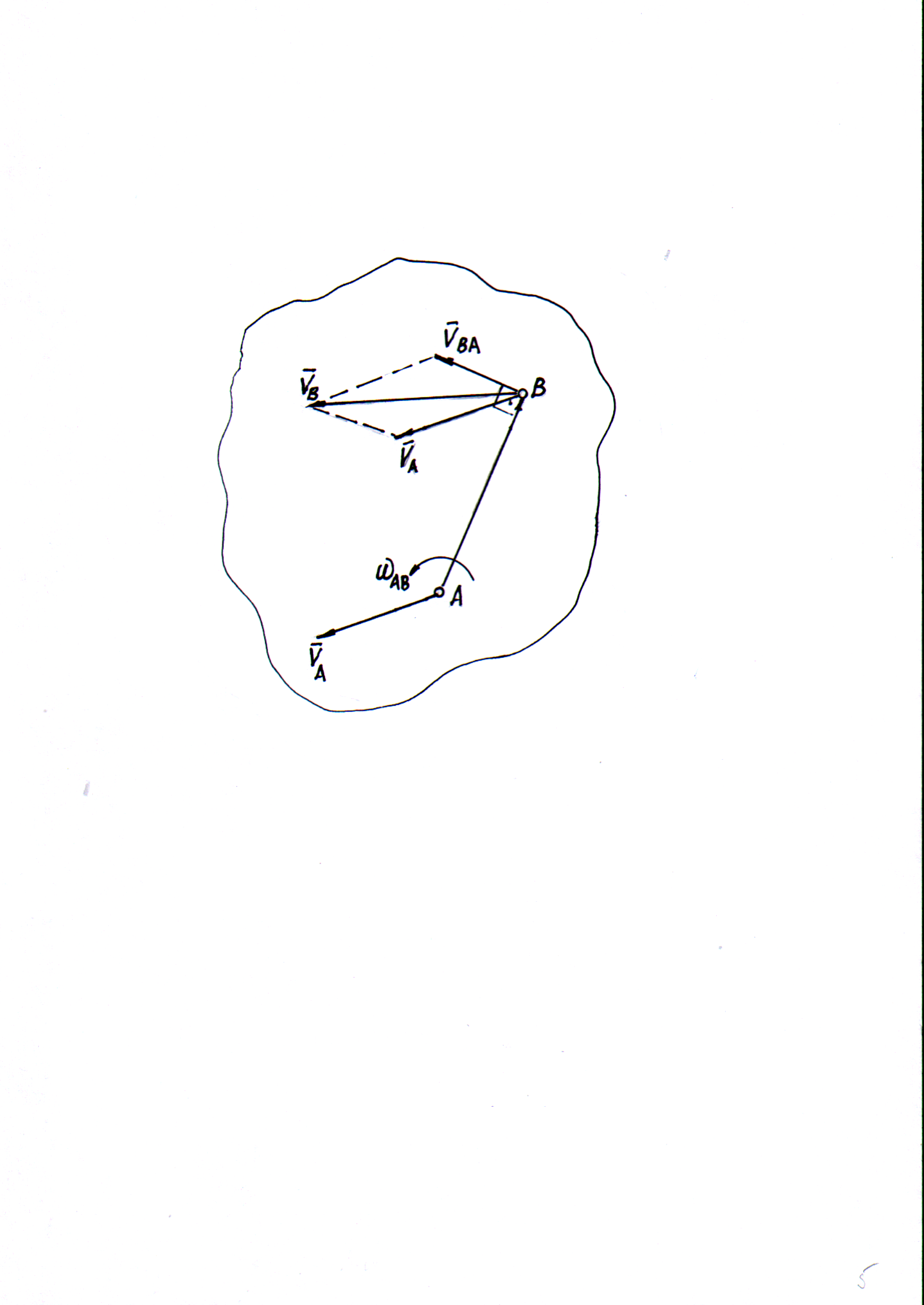
Рис. 5

Так как вектор перпендикулярен отрезку АВ (рис. 5), то из формулы (34) следует теорема: «Проекции скоростей двух точек сечения тела (плоской фигуры) на прямую, соединяющую их, равны». Если обозначить угол с направлением вектора скорости и прямойчерез, а с направлениемчерез, то получим выражение этой теоремы в виде

. (35)

Из формулы (31) следует, что если за полюс выбрать точку, скорость которой в данный момент времени равна нулю, то формула (31) упростится. Если тело не совершает поступательного движения, то такая точка существует, и притом одна. Ее называют мгновенным центром скоростей (МЦС) и часто обозначают через Р (рис. 6). Тогда для произвольной точки М сечения тела можно записать выражение ее скорости в виде

(36)

и по модулю она равна

. (37)

МР – расстояние точки М до мгновенного центра скоростей. Вектор скорости направлен перпендикулярно отрезкув сторону поворота плоской фигуры.

В общем случае мгновенный центр скоростей находится в точке пересечения перпендикуляров, проведенных через две точки сечения тела к направлению их скоростей.

ν_M

ν_N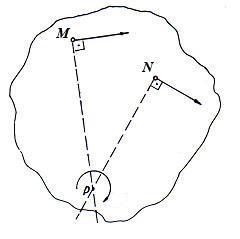



Рис. 6

Имеются частные случаи определения положения мгновенного центра скоростей (МЦС).

1. При качении без скольжения плоской фигуры по неподвижной поверхности, МЦС (точка P, рис. 7) находится в точке контакта поверхностей.

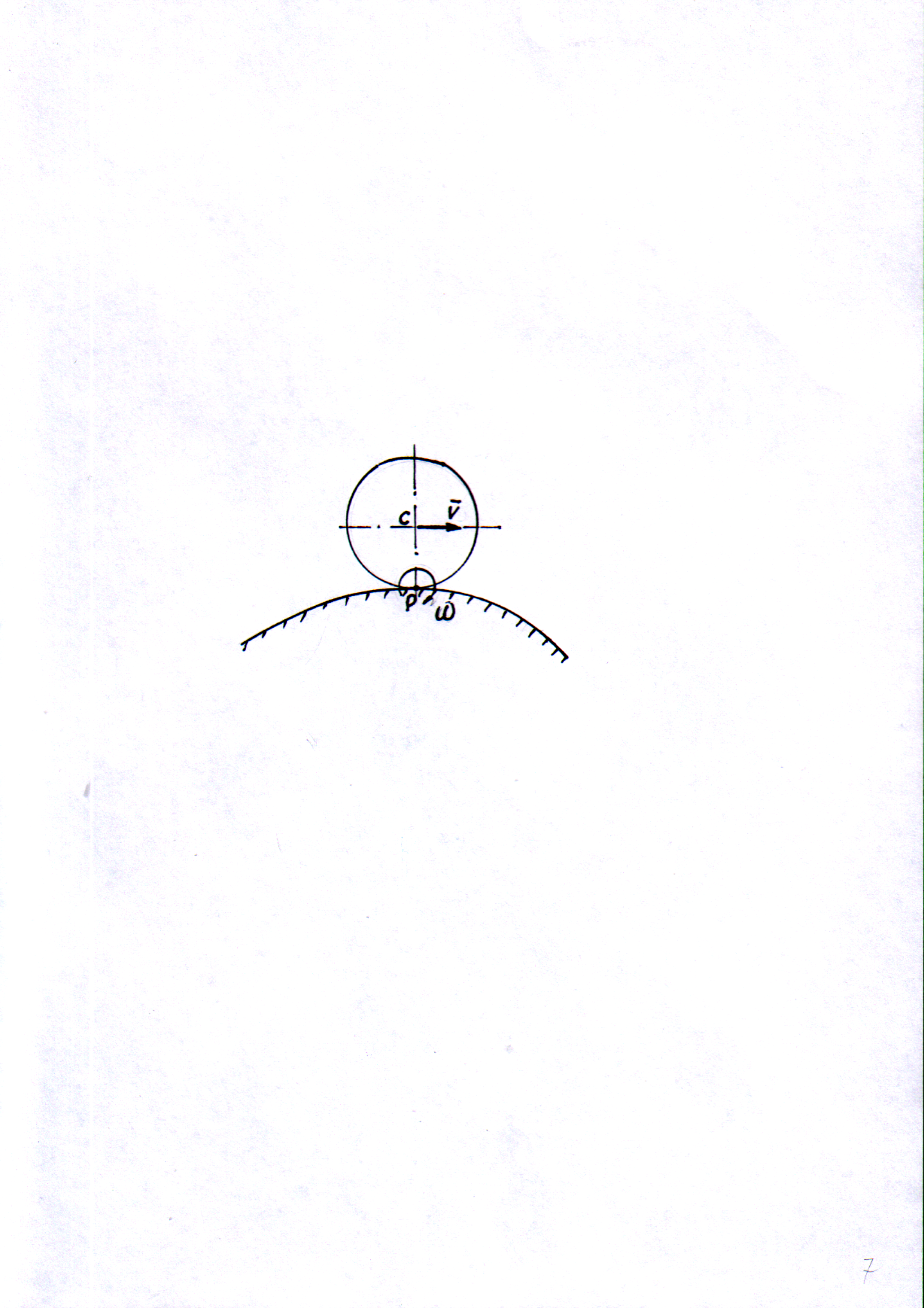
Рис. 7

2. Направление скоростей двух точек сечения тела имеют к ним общий перпендикуляр (рис. 8).

а)

б)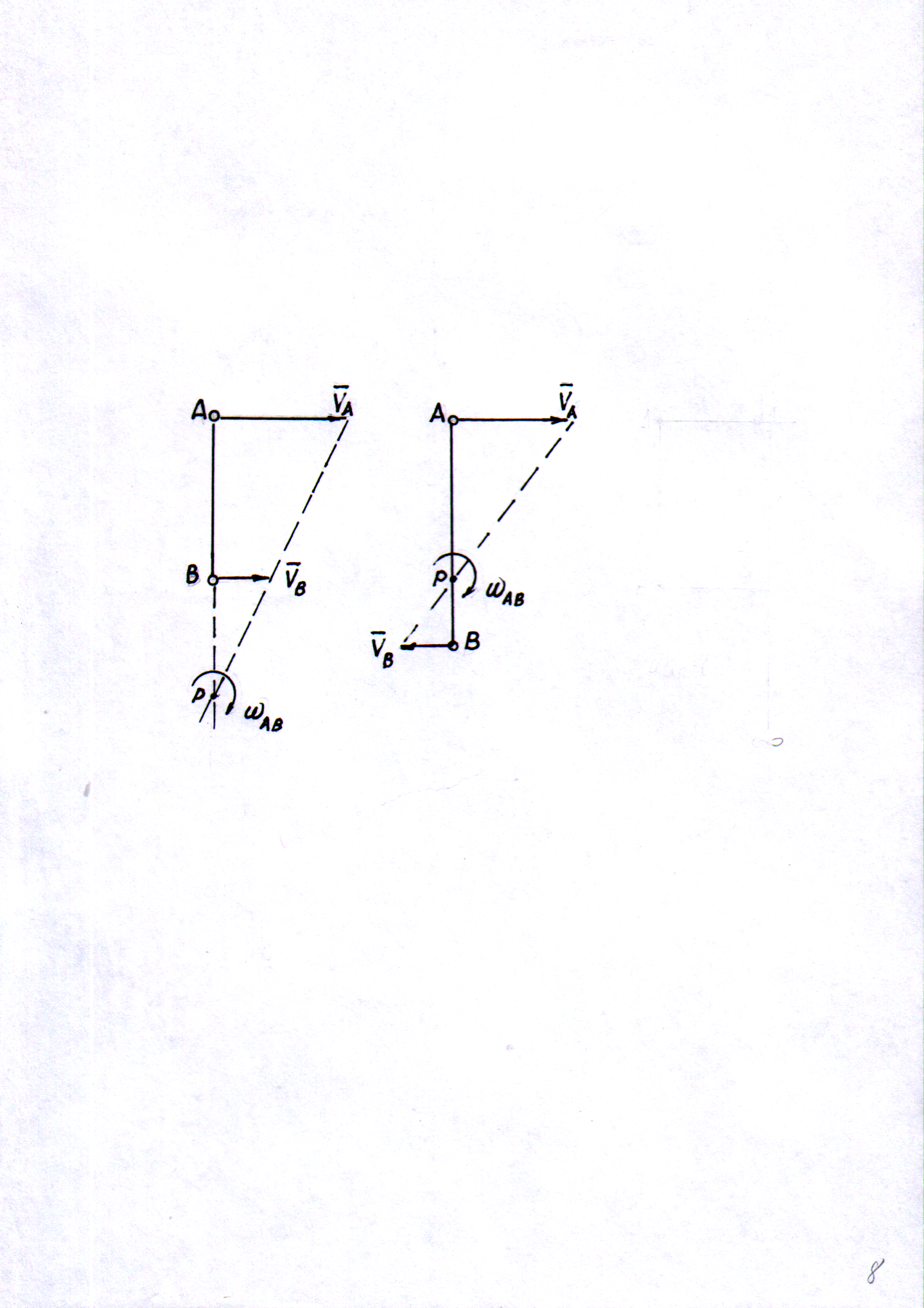

Рис. 8

В этом случае используют пропорциональность модуля скорости точек сечения тела их расстоянию до МЦС. Обозначим модуль скорости точки А через , точки В черези расстояние между точками равным АВ, тогда можно определить угловую скорость телаω:

- в случае одинакового направления скоростей и >(рис. 8,а)

, (38)

- в случае противоположного направления скоростей (рис. 8, б)

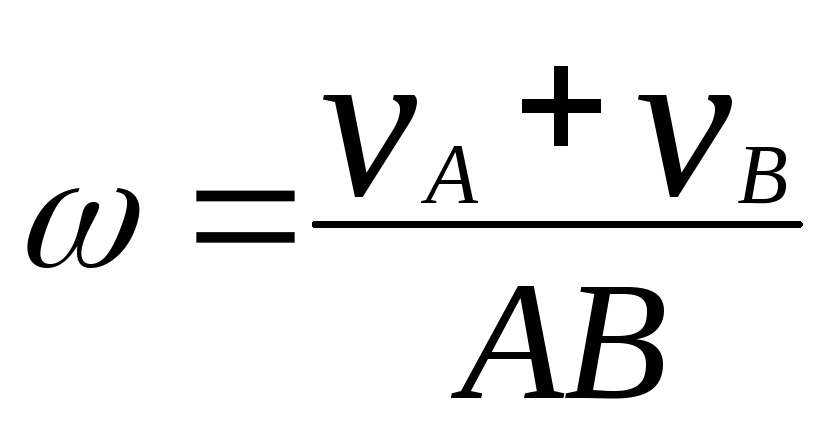. (39)

Тогда расстояние от этих точек до МЦС, то есть его положение на общем перпендикуляре к скоростям, определяется формулами

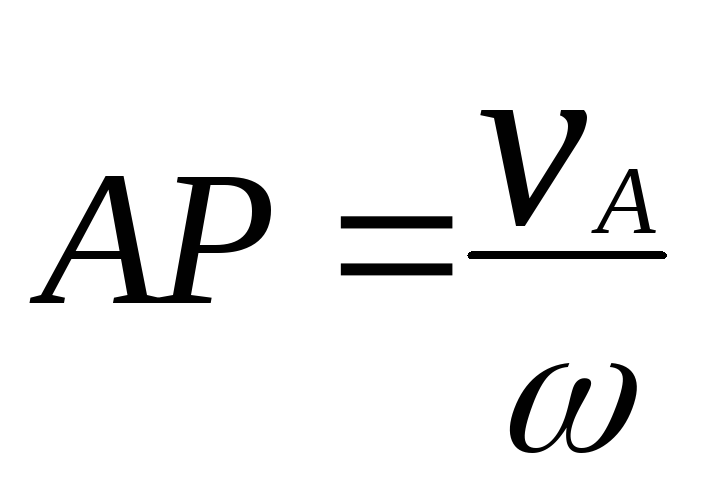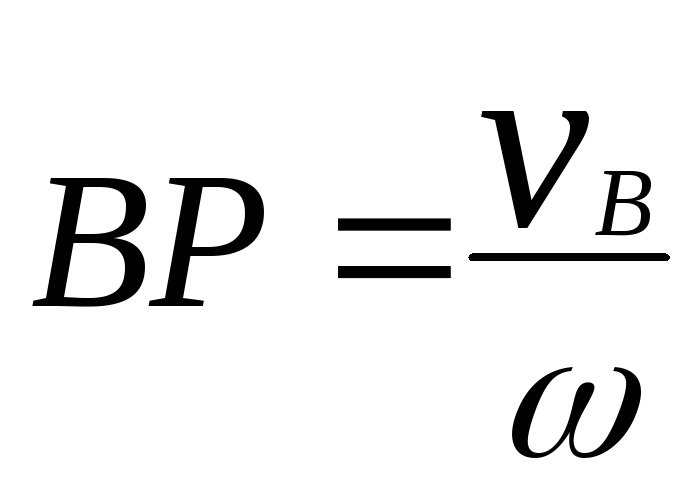,. (40)

3. Если перпендикуляры к скоростям двух точек сечения тела пересекаются в бесконечности или скорости точек равны, то тело совершает мгновенно поступательное движение, его угловая скорость ω равна нулю, и все точки тела имеют одинаковые скорости (рис. 9).

Рис. 9

Скорость точки можно определить и в аналитической форме на основании формул (30), то есть через проекции вектора скорости точки на неподвижные оси координат:

, (41)

. (42)

В этих формулах – искомые скорости точки М в проекциях на неподвижные оси координат;– проекции скорости полюса на неподвижные оси;– угловая скорость плоской фигуры;координаты полюса А и точки М в неподвижной системе координат соответственно. Модуль скорости точки М по известным проекциям определяется формулой

. (43)

Определение ускорения точки при плоском движении тела

Взяв от уравнения (34) производную по времени, получим теорему о распределении ускорений точек при плоском движении тела:

. (44)

Из формулы (44) следует: «Ускорение точки плоской фигуры складывается из ускорения полюса и ускорения при вращательном движении вокруг полюса».

В этой формуле полное ускорение произвольной точки В плоской фигуры;ускорение полюса;центростремительное ускорение при вращении фигуры вокруг полюса и направлено к полюсу;вращательное ускорение вокруг полюса и направлено перпендикулярно прямой АВ в сторону направления углового ускорения ;ускорение точки В при вращении плоской фигуры вокруг полюса А (рис. 10). При этом

, . (45)

, . (46)

В векторной форме ускорение

, (47)

а по модулю оно равно

. (48)

Это ускорение из точки В направлено под углом к лучу ВА, тангенс угларавен

. (49)

Из уравнений (41),(42) можно получить ускорения точки в аналитической форме, то есть через проекции на неподвижные оси координат:

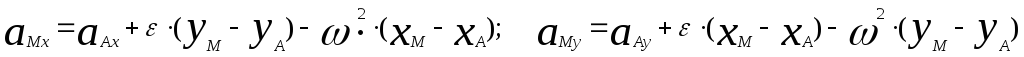; (50)

.

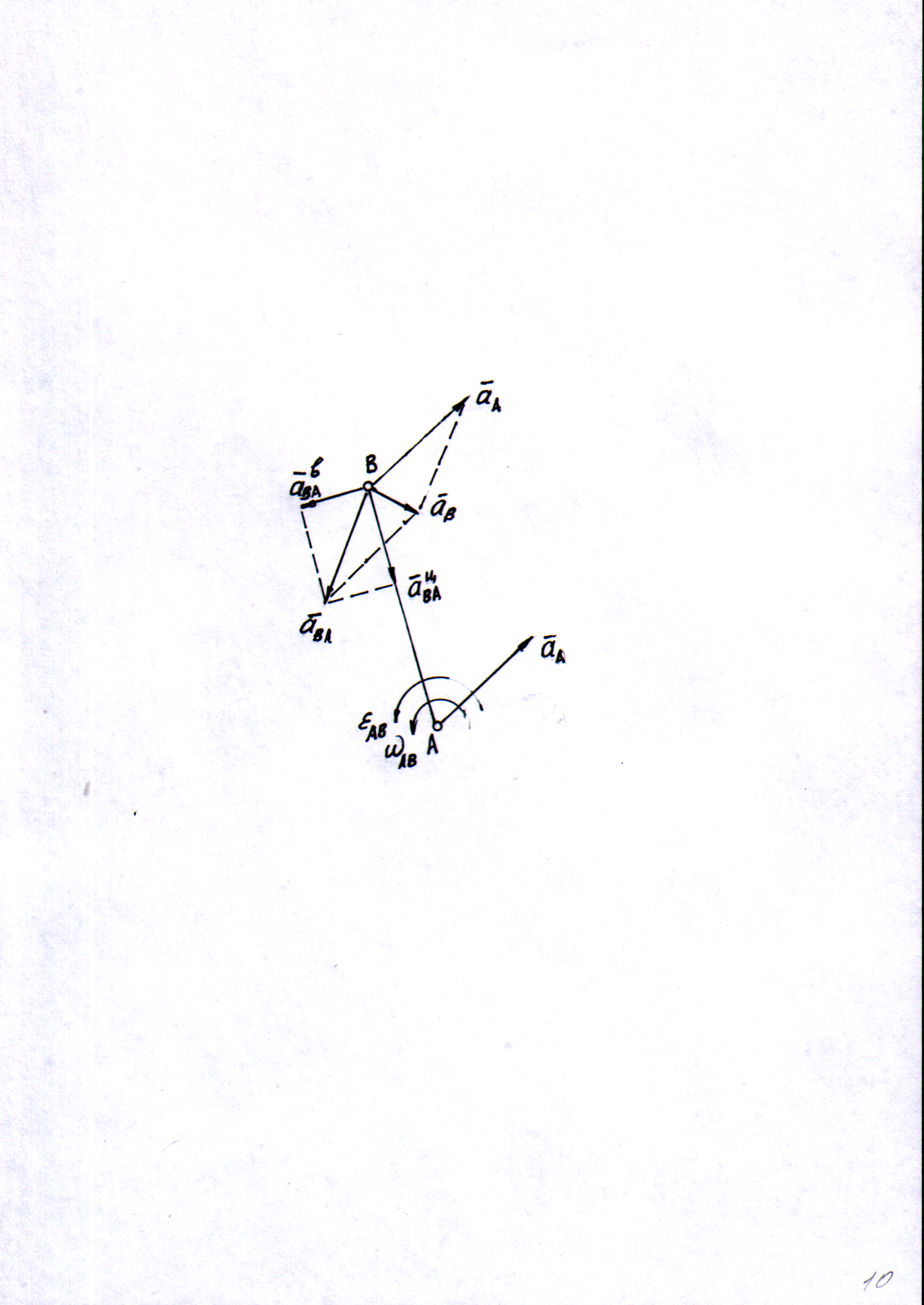
Рис. 10