
21869_4f7d312f91bac43d4530a115cb0453bf
.pdf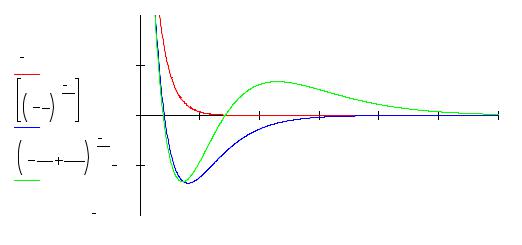
g = a1 ρ + a2 ρ2 + a3 ρ3 = ρ − 2 ρ2 / 3 + 2 ρ3 / 27, |
|
|
|
|||||||||
ϕ = (1 - 2ρ/3 |
|
+ 2 ρ2/27) e - ρ / 3. |
|
|
|
|
|
|||||
График зависимости |
ϕn (ρ) имеет вид для трех значений |
n = 1,2,3 такой, что с |
||||||||||
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
e ρ |
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
1 |
|
ρ |
. 2 |
|
|
|
|
|
|
|
|
|
|
2 |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
|
|
|
|
ρ |
|||||||
|
|
. |
. 2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
||
1 |
ρ |
2 ρ . |
|
|
|
|
|
|
|
|
||
3 |
e |
|
0.1 |
|
|
|
|
|
|
|||
|
27 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
ρ |
|
|
30 |
ростом ρ возрастает количество корней и экстремумов |
|
|||||||||||
Напомним, что при ρ = 1 расстояние соответствует Боровскому радиусу. |
||||||||||||
§ 6 Смысл ψ - функции и соотношение неопределенностей |
|
|||||||||||
6.1 О смысле ψ - функции |
|
|
|
|
|
|||||||
Итак, электрон в атоме частица-волна. Опыты по интерференции Дэвиссона и Джермера (1927) показали, что даже при пропускании по одному электрону при достаточной экспозиции (а не только сколько-нибудь существенного пучка) через кристалл никеля возникала интерференционная (или дифракционная) картина. Это доказывает, что и отдельные частицы обладают волновыми свойствами.
При прохождении соответствующей электронной волны через кристалл, она разбивается на несколько дифракционных пучков. Трудно допустить, что в каждом из пучков находится какая-то доля электрона. При этом счетчик электронов срабатывает по предположению при попадании в него целого электрона.
410
x |
x |
x |
датчик |
|
|
источник |
|
|
экран |
|
|
(1) |
(2) |
(3) |
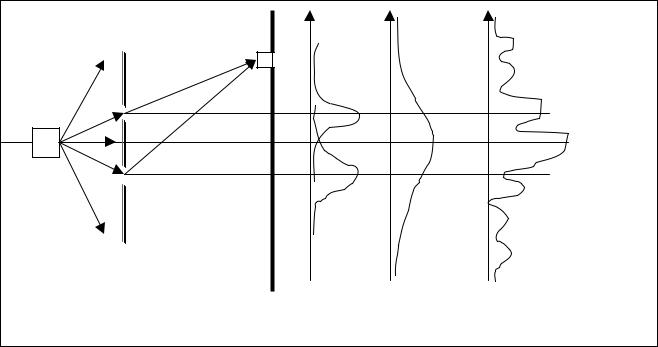
Результат взаимодействия пуль (частиц) и волн |
||
Пусть из источника вначале стреляют пулями (1) и (2) , а затем, по мере надобности источник можно заменить на источник волн (или электронов, так как экспериментально доказаны их волновые свойства). График (1) – результат поочередного открывания щелей. Он одинаков для пуль, волн и электронов. График (2) описывает поведение интенсивности на экране, если открыть обе щели. Для пуль интенсивности просто сложатся. График (3) иллюстрирует поведение результирующей интенсивности. Если открыть обе щели для волн (и электронов) получится интерференционная картина. (Заметим, забегая вперед, что суть противоречивости явления описываемого соотношениями неопределенностей Гейзенберга (о невозможности одновременно точного знания координаты и импульса объекта) скрыты именно в этом противоречии поведения волн и пуль).
Для волн мы имели
I1 ~ E12, I2 ~ E22, E2 = E12 + E22 + 2E1E2 Cos δ, Ι = Ι1 + Ι2 + √Ι1Ι2 Cosδ.
тогда
I |ψ|2 ψψ , действительно |ψ|2 = | e iωt + α |2 = | e iωt|2 e 2α = e 2α.
ψψ* = e iωt + α e - iωt + α = e 2α.
Дифракционная (так же как и интерференционная) картина для микрочастиц является проявлением статистической (вероятностной) закономерности,
412


Глава 4 Атомная физика твердых тел
§ 1 Типы связей атомов в твердых телах
Рассмотрим процессы объединения отдельных атомов в твердые тела, когда в один см3, например, объединяются несметные количества атомов. Рост кристаллов как известно возможен из растворов и расплавов веществ. Отвердевание расплава происходит при его охлаждении. При этом от расплава отбираются, откачиваются горячие молекулы. Проследим процесс объединения атомов с энергетической точки зрения.
1. Атомы разведены достаточно далеко. Они свободны
Eсвоб = Σ Ei своб.
Их суммарная энергия складывается из энергии каждого атома.
2.Атомы сведены в твердое тело. Это им оказывается энергетически более выгодно и тогда
Eсвяз < Eсвоб.
Сравнительно не плотно упакованы атомы цезия в твердом теле n = 0,91 1022 см – 3. Довольно плотно упакованы атомы бериллия n = 24,7 1022 см – 3. Что удерживает атомы вместе ? Эти силы – электрические. Перечислим типы связей атомов в твердых телах.
416
1.Ионная связь (гетерополярная) – притяжение положительных и отрицательных ионов друг к другу. NaCl, Li F, K J и др. Энергию связи называют еще когезионной энергией.
Таблица когезионных энергий ионных кристаллов
|
|
|
|
|
|
|
|
Ec, 10 – 18 |
Li |
|
Na |
k |
Rb |
Cs |
|
Дж/молекулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
1,68 |
1,49 |
|
1,32 |
1,26 |
1,20 |
|
|
|
|
|
|
|
|
|
Cl |
1,38 |
|
1,27 |
|
1,15 |
1,11 |
|
|
|
|
|
|
|
||
Br |
1,32 |
1,21 |
1,10 |
1,06 |
|
||
|
|
|
|
|
|
|
|
I |
1,23 |
1,13 |
|
1,04 |
|
|
|
|
|
|
|
|
|
|
|
Рассчитаем когезионную энергию, приходящуюся на 1 моль NaCl: E = Ec NA = 1,27 10 – 18 6,02 10 23 = 750 кДж.
2.Ковалентная или атомная связь (гомеополярная) – строение решетки, при котором число атомов ближайших к рассматриваемому атому равно валент-
ности элемента. Валентные электроны атомов обобществлены (происходит насыщение валентности). Когезионная энергия составляет 700-1200 кДж/моль.
3.Молекулярная связь (связь сцепления – слабая связь без насыщения валентности) – обусловлена силами Ван-дер-Ваальса. Почти все органические кри-
сталлы, кристаллы из инертных газов, например Hg2, Ar, CH4 . Когезионная энергия – 8 кДж/моль.
4.Металлическая связь – обобществлены 1-2 внешних электрона недостроенных оболочек. Эти электроны слабо связаны со своим элементом, обобществлены и ведут себя в кристалле подобно электронному газу. Между положительными ионами действуют силы отталкивания, а электроны уравновешивают эти силы и удерживают ионы в равновесии. Эти подвижные электроны обусловливают очень высокую электро- и теплопроводность металлов. (За-
417
метим, что сжиженные инертные газы также образуют металлическую связь и при сверхнизких температурах становятся металлоподобными. Так как они сферически высоко симметричны, то пришлось предположить при Т=0°К наличие так называемых нулевых колебаний (чтобы объяснить их способность объединяться в металлоподобную молекулу)).
5.Отметим отдельно водородную связь. Устройство атома водорода сходно с
устройством атомов металлов, но имеет следующие особенности:
Ионный остаток Н – голый протон размером 10 – 13 см (1 F), в 105 раз меньше любого ионного остатка Водороду не хватает одного электрона для заполнения до устойчивой двух
электронной оболочки (как у Не)
Первый потенциал ионизации относительно очень высок: 13,59 эВ != 2 10 – 18
Дж / атом = 1200 кДж/моль. Связь в Н2 похожа на ковалентную, но образует лишь одну ковалентную связь.
§ 2 Дифракция рентгеновских лучей
По Брэггам У.Г. и У.Л. (1913г.) – кристаллы дают характерную картину рентгеновского излучения: для некоторых длин волн и направлений падения лучей наблюдаются интенсивные максимумы рассеянного излучения.
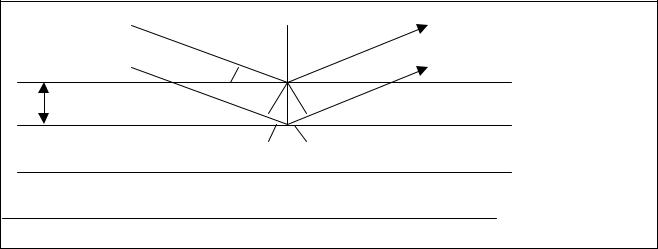
Представим себе кристалл, состоящим из симметрично расположенных образований (атомов)
• |
• |
• |
θ |
• |
• |
• |
d |
|
|
|
θ |
|
|
• |
• |
• |
|
• |
• |
• |
|
|
|
|
d Sin θ |
|
|
• |
• |
• |
|
• |
• |
• |
• |
• |
• |
|
• |
• |
• |
Подсчет разности хода для двух разных лучей, отраженных от смежных плос- |
||||||
костей дает |
2 d Sinθ , тогда условие максимума интерференции запишется в |
|||||
виде |
|
|
|
|
418 |
|
|
|
|
|
|
|
|

2d Sinθ = n λ.
Это равенство называется формулой Вульфа - Брэггов.
По Лауэ кристалл состоит из тождественных объектов (атомов, групп атомов), размещенных в узлах решетки и каждый объект может рассеивать падающее на него излучение. Надо искать точки, в которых ощутим результат интерференции. Для удобства описания кристаллических структур были введены понятия прямой и обратной решетки, решетки Бравэ. Можно также говорить о примитивной решетке – ячейке Вигнера-Зейтца. Эти понятия справедливы как в обычном трехмерном пространстве, так и в пространстве обратном линейному трехмерному. Элементарную ячейку Вигнера-Зейтца для обратной решетки называют зоной Бриллюэна. Пусть G – вектор трансляции обратной решетки
G = k1b1 + k2b2 + k3b3.
Согласно Лауэ расчеты интерференции максимумов производятся в к – пространстве (пространстве волновых векторов)
k |
|
k′ |
|
k′ |
|
|
|
|
|
|
|
• |
||
d Cosθ = d n |
|
θ d |
k |
|
• |
θ′ |
|||
|
|
d Cosθ′ = - d n |
|
|
Для конструктивной интерференции (образования максимума) необходимо, чтобы изменение волнового вектора K = k - k′ было равно одному из векторов обратной решетки. Разность хода двух лучей, смещенных друг относительно друга на постоянную решетки, равна
d Cosθ + d Cosθ′ = d (n - n′).
n, n′ - орты волновых векторов k, k′. Тогда условие конструктивной интерференции в прямом пространстве имеет вид
d(n-n′) = mλ.
419
