Критерий Сэвиджа

В соответствии с (4) добавим к исходной матрице выигрышей строку столбцовых максимумов ^j (таблица 6.8).

Таблица 6.8 – Матрица выигрышей
	B1	B2	B3	B4
A1	7	5	1	10
A2	5	2	8	4
A3	1	3	4	12
A4	8	5	1	10
j	8	5	8	12

Преобразуем матрицу выигрышей в матрицу рисков (таблица 6.9).

Таблица 6.9 – Матрица рисков
	B1	B2	B3	B4	max
A1	1	0	7	2	7
A2	3	3	0	8	8
A3	7	2	4	0	7
A4	0	0	7	2	7

В столбце max содержатся строчные масимумы, которые характеризуют наибольший риск при выборе соответствующей альтернативы.

Выбираем альтернативу, минимизирующую максимальный риск:

min (7, 8, 7, 7) = 7. Оптимальными являются альтернативы A₁, A₃, A₄.

7. Принятие решений в условиях риска

Дано: X — множество допустимых альтернатив, X  = n;

Y — множество состояний среды, Y  = m;

A — множество исходов, A  = n  m;

F: X  Y  A — функция реализации;

На множестве состояний среды Y, Y= m задана вероятностная мера. Она задана вероятностным вектором y = (y₁, y₂, …, y_m), y_i ≥ 0,

где y_j, — вероятность наступления состояния j.

Матрица выигрышей имеет вид (таблица 7.1):

Таблица 7.1 – Матрица выигрышей
	Состояние среды
Альтернатива	y1 1	…	yj j	…	ym m
1	a11	…	a1j	…	a1m
…	…	…	…	…	…
i	ai1	…	aij	…	aim
…	…	…	…	…	…
n	an1	…	anj	…	anm

Выбирая альтернативу i, игрок знает, что получит один из выигрышей a_i¹, …, a_i^m с вероятностями y₁, …, y_m соответственно.

Таким образом, исходом для ЛПР при выборе им альтернативы i является случайная величина

	ai1, …, aim
i =
	y1, …, ym

Поэтому сравнение двух альтернатив i₁ и i₂ сводится к сравнению случайных величин ₁ и ₂.

7.1. Построение обобщённого критерия

Случайная величина _i может быть охарактеризована парой показателей (M_i, _i), где M_i = M_i — математическое ожидание случайной величины _i, а _i = — среднеквадратическое отклонение.

В теории вероятностей в качестве «меры разброса» берётся дисперсия D или среднеквадратическое отклонение _i = .

D = M( - M)²= M² – (M)².

Получили задачу двухкритериальной оптимизации, где в качестве критериев имеем M и .

Единый критерий имеет вид: q(M, ) = M - λ, где λ – некоторая константа.

При этом, критерий M — позитивный, а критерий  — негативный.

При λ > 0 оценка случайной величины : q < M, что характерно для осторожного человека, не склонного к риску.

При λ < 0: q > M, что характеризует человека, склонного к риску.

При λ = 0: q = M, что характеризует человека, безразличного к риску.

Таким образом, λ — это субъективный показатель меры несклонности к риску ЛПР.

Как сравнивать альтернативы по обобщённому критерию q?

Пусть имеются две альтернативы:

Рассмотрим два случая:

а) Альтернативы и сравнимы по Парето, например  . Тогда ≥ и ≤ .

б) Альтернативы и не сравнимы по Парето. Например, при

> , > – больший ожидаемый выигрыш связан с большим риском. Условие - > - равносильно тому, что .

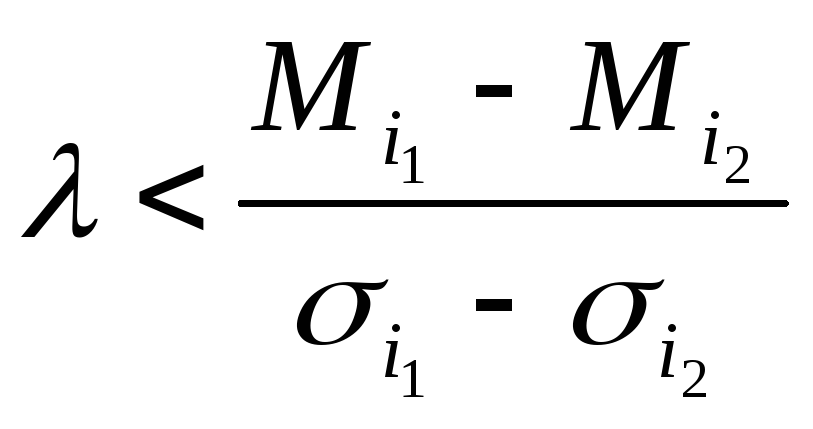Таким образом: , если

Обозначим: ,

,

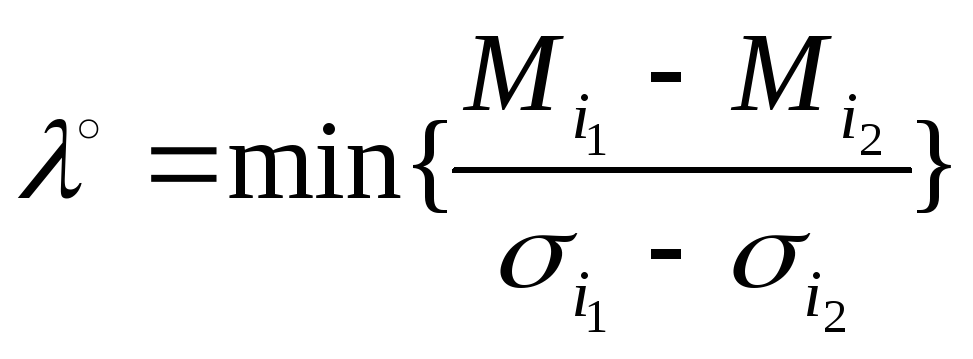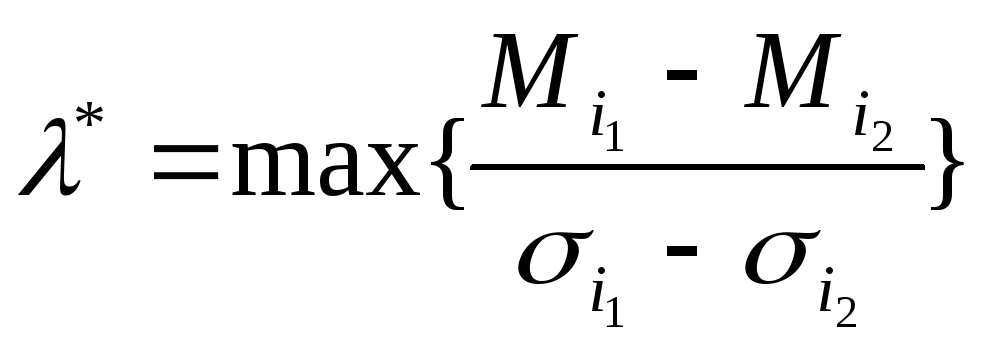где - нижняя граница несклонности к риску;

- верхняя граница несклонности к риску.

Таким образом, для ЗПР в условиях риска применение обобщённого критерия q сводит проблему нахождения оптимального решения к проблеме установления для ЛПР его меры несклонности к риску λ.