01 КАСЮК С. Т. ПЕРВИЧНЫЙ, КЛАСТЕРНЫЙ, РЕГРЕССИОННЫЙ И ДИСКРИМИНАНТНЫЙ АНАЛИЗ ДАННЫХ СПОРТИВНОЙ МЕДИЦИНЫ НА КОМПЬЮТЕРЕ

будет простое среднее значение yср = 16. Рассмотрим рисунок 3.2, на котором оценка пройденного расстояния, не учитывающая информацию о времени в пути, представлена горизонтальной линией yср = 16.

Отсутствие информации о времени приводит к оценке пройденного расстояния 16 км как для участников, которые идут только 2-3 часа, так и для тех, кто идет уже 8–9 часов. Очевидно, что корректность такой оценки сомнительна.

Рисунок 3.2 – Геометрическая интерпретация линии регрессии

Точки на рисунке 3.2 сосредоточены вдоль линии регрессии, а не вдоль линии уср = 16. Суммарная ошибка оценивания здесь будет меньше, если использовать информацию о времени. Например, рассмотрим участника под номером 10, который прошел дистанцию у = 25 км за 9 часов. Если игнорировать информацию о времени и предположить, что он, как и все остальные, прошел только 16 км, то ошибка оценивания составит E 10 = y – y c p = 25 – 16 = 9 км.

Мы можем сравнить стандартную ошибку ˆ = 1,1 и ошибку, полученную

Ест

при использовании в качестве оценки среднего значения ус р = 16, когда информация о предсказывающей переменной игнорируется:

Таким образом, типичной ошибкой предсказания для случая, когда информация о значениях предсказывающей переменной не используется, будет 4,74 км. Следовательно, применение регрессии вместо оценки на основе простого среднего значения позволяет уменьшить ошибку с 4,74 до 1,1 км, то есть более чем в 4 раза. Это позволяет сделать вывод о значимости полученной регрессионной модели. Если бы значения стандартной ошибки, полученные для оценок регрессии и простого среднего значения, были примерно одинаковы, это говорило бы о том, что регрессия практически не дает выигрыша в точности оценки по сравнению с обычным средним наблюдаемых значений, то есть о низкой значимости регрессионной модели [8].

Изменчивость выходной переменной. Для оценки степени соответствия регрессии реальным данным используются три квадратичные суммы: общая ЕT, регрессионная ER и ошибки ЕE [8].

Квадратичные суммы вычисляются по следующим формулам (32):

Квадратичные суммы связаны между собой следующим отношением (33):

ЕT = ER + ЕE. (33)

Полная изменчивость выходной переменной складывается из части, объясненной регрессией, и ошибки, то есть части, не объясненной регрессией.

Коэффициент детерминации – статистический показатель, отражающий объясняющую способность уравнения регрессии и являющийся статистической мерой согласия, с помощью которой можно определить, насколько уравнение регрессии соответствует реальным данным [8].

Коэффициент детерминации r2 показывает степень согласия регрессии как приближения линейного отношения между входной и выходной переменными с реальными данными (34):

Значение коэффициента детерминации максимально, когда имеет место идеальное соответствие: все точки данных лежат точно на прямой регрессии. В этом случае ошибка ЕЕ оценки, полученной с помощью регрессии, равна 0. Тогда ЕТ = ЕR и r 2 = 1. Максимальное значение коэффициента детерминации, равное 1, имеет место только тогда, когда уравнение регрессии идеально описывает связь между входной и выходной переменными [8].

Чтобы определить минимальное значение коэффициента детерминации, предположим, что регрессия совсем не улучшает точность оценки по сравнению с использованием среднего значения, то есть не объясняет изменчивость выходной переменной. В этом случае ЕR = 0, а значит, и r 2 = 0. Таким образом, коэффициент детерминации может изменяться от 0 до 1 включительно. При этом чем выше значение r 2 , тем больше регрессионная модель соответствует реальным данным.

72

Значения r 2 , близкие к 1, означают очень хорошее соответствие регрессионной модели реальным данным, а значения, близкие к 0, – очень плохое.

Значение коэффициента детерминации для рассмотренного примера из табицы 3.2 будет равно 0,95. Поэтому можно сделать вывод, что регрессионная модель работает хорошо.

Коэффициент корреляции является ещѐ одной мерой, используемой для количественного описания линейной зависимости между двумя числовыми переменными. Он определяется следующим образом (35):

где x и y – стандартные отклонения соответствующих переменных.

Значение коэффициента корреляции всегда расположено в диапазоне от –1 до 1 включительно и может быть интерпретировано следующим образом:

1 Если коэффициент корреляции близок к 1, то между переменными наблюдается сильная положительная корреляция. Иными словами, наблюдается высокая степень зависимости входной и выходной переменных (если значения входной переменной х возрастают, то и значения выходной переменной у также будут увеличиваться).

2 Если коэффициент корреляции близок к –1, это означает, что между переменными наблюдается отрицательная корреляция: поведение выходной переменной будет противоположным поведению входной (когда значение х возрастает, у уменьшается, и наоборот).

3 Промежуточные значения указывают на слабую корреляцию между переменными и, соответственно, на низкую зависимость между ними: поведение входной переменной х совсем (или почти совсем) не будет влиять на поведение у.

Для приближенной оценки коэффициента корреляции можно воспользо-

Для вычисления коэффициента корреляции можно использовать коэффици-

ент детерминации r 2 , то есть r 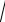r2 . Если коэффициент уравнения регрессии b1 > 0 (линия регрессии возрастает), то и коэффициент корреляции также будет

положительным, то есть r r2 . В противном случае коэффициент корреляции

будет отрицательным, то есть r r2 .

Для рассмотренного примера b1 = 2, коэффициент корреляции будет положительным и равным 0,97.

73

где tT – табличное значение критерия Стьюдента при уровне значимости α и числе степеней свободы v = n – p.

Таким образом, для оценки значимости коэффициента уравнения регрессии

рассчитанное значение критерия Стьюдента tˆ сравнивают с его табличным значением tT при выбранной доверительной вероятности 1 – α, где α – уровень

значимости, и числе степеней свободы v = n – р. Если вычисленное значение tˆ выше, чем табличное, то коэффициент регрессии является значимым с заданной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной xj из регрессионной модели.

Доверительную вероятность выбирают, как правило, 0,95. Критические точки распределения Стьюдента для различных уровней значимости α приведены в приложении Е.

3.5 Значение остатков при изучении результатов регрессионного анализа

Остатки представляют собой разницу между наблюдаемым значением функции отклика yi в точках, в которых измеряется значение функции, и предсказывае-

Остатки используют в первую очередь для вычисления остаточной дисперсии, но в них содержится и другая информация. Остатки – это то, что нельзя объяснить уравнением регрессии, их можно квалифицировать как «шум», помехи или погрешности, если само уравнение получено правильно [9].

При проведении регрессионного анализа считают, что остатки независимы,

имеют нулевые средние, одинаковую (постоянную) дисперсию и подчиняются за-

кону нормального распределения. Подтверждение перечисленных свойств остатков служит доказательством того, что модель построена правильно.

Следовательно, прежде всего проверяют условие (42)

и затем проверяют нормальность распределения остатков.

Нарушение закона нормального распределения остатков может означать следующее [9]:

1)дисперсия остатков не является постоянной – необходимо учесть неодно-

родность наблюдений или преобразовать исходные данные до начала обработки;

2)анализ ошибочен – отклонения от уравнения регрессии носят систематический характер: большим значениям yˆi соответствуют большие отклонения εi , и

наоборот; 3) модель неадекватна – необходимо внести дополнительные члены или

преобразовать исходные данные до начала анализа.

75

3.6 Пример проведения регрессионного анализа в пакетe STATISTICA 10

Проведем регрессионный анализ данных примера о спортивном соревновании (таблица 3.2). Рассчитаем коэффициенты уравнения регрессии, определим статистические показатели модели, проверим остатки.

Алгоритм решения:

1 Создадим новую таблицу: вкладка Home (Главная) – группа File (Файл) –

команда New (Создать). В окне Create New Document (Создать новый документ)

во вкладке Spreadsheed (Рабочий лист) введем следующие параметры:

–в поле Number of variables (Количество переменных) – 2;

–в поле Number of cases (Количество наблюдений) – 10. Нажимаем кноп-

ку ОК.

2 Введем исходные данные из таблицы 3.2 в отдельные столбцы, соответствующие переменным.

3 На вкладке Statistics (Анализ) в группе Base (Базовая статистика) выберем команду Multiple Regression (Множественная регрессия).

4 В появившемся стартовом окне модуля Multiple Regression (Множест-

венная регрессия) (рисунок 3.3) нажимаем кнопку Variables (Переменные).

Рисунок 3.3 – Стартовое окно модуля

Multiple Regression (Множественная регрессия)

76

5 Откроется диалоговое окно Select dependent and independent variable lists

(Список зависимых и независимых переменных) (рисунок 3.4). Выберем Рас-

стояние y в качестве зависимой переменной (Dependent var.), а Время х в качестве независимой переменной (Independent variable). Нажимаем ОК, чтобы вер-

нуться в окно Multiple Regression (Множественная регрессия).

Рисунок 3.4 – Диалоговое окно

Select dependent and independent variable lists

(Список зависимых и независимых переменных)

6 Переменные выбраны, запустим вычислительную процедуру, нажав кнопку ОК.

7 На экране появится окно Multiple Regression Results (Результаты множе-

ственной регрессии), содержащее информационную часть и вкладки, представляющие способ отображения результатов (рисунок 3.5).

8 В информационной части этого окна содержится следующие описание модели и краткие сведения о результатах (рисунок 3.5):

–Dependent (Зав. перем.) – зависимая переменная.

–No. of cases (Число набл.) – число наблюдений в таблице.

–Multiple R (Множеств. R) – коэффициент множественной корреляции.

–R2 – квадрат коэффициента множественной корреляции, называемый также коэффициентом детерминации. Коэффициент детерминации является одной из основных статистик в данном окне, он показывает долю общего разброса, которая объясняется построенной регрессией.

–Adjusted R2 (Скоррект. R2) – скорректированный коэффициент детерминации, определяемый как (43):

77

где n – число наблюдений в модели; p – число параметров модели (p = k + 1).

–Standard error of estimate (Стандартная ошибка оценки) – мера рассея-

ния наблюдаемых значений относительно регрессионной прямой.

–Intercept (Св. член) – оценка свободного члена, значение коэффициента b0 в уравнении регрессии.

–Std.Error (Ст. ошибка) – стандартная ошибка оценки свободного члена – стандартная ошибка коэффициента b0 в уравнении регрессии.

–t и p – значение t-критерия и уровень p, t-критерий используется для проверки гипотезы о равенстве 0 свободного члена регрессии.

–F – значение F-критерия.

–df – число степеней свободы F-критерия.

– p – уровень значимости.

Рисунок 3.5 – Окно Multiple Regression Results

(Результаты множественной регрессии)

78

9 В информационной части окна рассмотрим прежде всего значение коэффициента детерминации R2, лежащее в пределах от 0 до 1. В рассматриваемом примере коэффициент детерминации высокий R2 = 0,94… Это значение показывает, что построенная регрессия объясняет более 94% разброса значений переменной Время х относительно среднего.

10 Рассмотрим значение F-критерия Фишера и уровень значимости p, которые используются для проверки значимости регрессии.

В окне приведено расчетное значение F-критерия ˆ = 144 при уровне зна-

F

чимости p = 0,000002 и степенях свободы v1 = 1 и v2 = 8. Табличное значение, взятое при уровне значимости α = 0,05 и степенях свободы v1 = 1 и v2 = 8 , равно

ляется значимой по F-критерию Фишера.

11 Рассмотрим вторую часть информационного окна. В этой части пакет STATISTICA 10 сам говорит о значимых регрессионных коэффициентах, высвечивая строку Bpемя x, ч b*=,973 красным цветом. Надпись significant b* are highlighted in red говорит о том, что значимый по критерию Стьюдента коэффициент выведен красным цветом.

12 Выберем представление результатов в виде таблицы, нажав кнопку

Summary: Regression results (Итоговая таблица регрессии). На экране появится итоговая таблица вывода, в которой представлены результаты регрессионного анализа (рисунок 3.6).

Впервом столбце таблицы даны значения коэффициентов b* (БЕТА) – стандартизированные коэффициенты регрессионного уравнения; во втором – стандартные ошибки Std. Err. of b* (Ст. Ош. БЕТА); в третьем – точные оценки параметров модели.

Оценка свободного члена b0 = 6,000000; коэффициент b1 = 2,000000. Основываясь на пролеченных расчетах получаем регрессионную модель:

Расстояние y = 6,000000 – 4,000000 · Время x.

Втаблице итогов регрессии также содержатся стандартные ошибки для коэффициентов регрессии b, значения статистик t-критерия и p-уровень. Значимые коэффициенты высвечены красным цветом.

Расчетное значение критерия Стьюдента tˆ = 12,000000 для коэффициента b1 сравниваем с его табличным значением tT = 2,31 при уровне значимости α = 0,05 и

числе степеней свободы v = N – p =8. Получили, что расчетное tˆ > tT , и следовательно коэффициент регрессии b1 является значимым с доверительной вероятностью 95%.

79

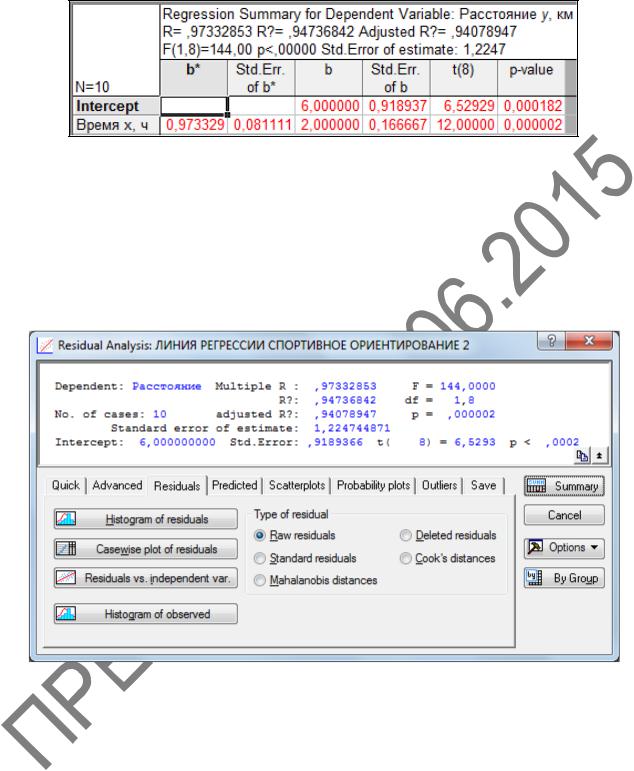
Рисунок 3.6 – Таблица итогов регрессии

13 Проанализируем остатки. Вернемся в окно результатов и выберем вклад-

ку Residuals/assumptions/prediction (Остатки/предсказанные/наблюдаемые значения) (рисунок 3.7) и нажмем на кнопку Perform residual analysis (Анализ остатков). В окне Residual analysis (Анализ остатков) можно просмотреть значение остатков и построить различные варианты диаграмм рассеяния.

Рисунок 3.7 – Окно Residual analysis (Анализ остатков)

14 Нажав на кнопку Casewise plot of residuals (Построчн. графики остат-

ков) выведем на экран таблицу с остатками регрессионной модели (рисунок 3.8). В этой таблице выделим столбец с остатками Residual (Остатки) и скопируем данные в буфер обмена, нажав сочетание клавиш Ctrl + C. Создадим новую таблицу: вкладка New (Главная) – группа File (Файл) – команда New (Создать) – вкладка Spreadsheed (Таблица). Вставим скопированные данные в столбец, соответствующий переменной Var 1, нажав сочетание клавиш Ctrl + V. Запускаем мо-

дуль Descriptive statistics (Описательные статистики): вкладка Statistics (Ана-

80