01 КАСЮК С. Т. ПЕРВИЧНЫЙ, КЛАСТЕРНЫЙ, РЕГРЕССИОННЫЙ И ДИСКРИМИНАНТНЫЙ АНАЛИЗ ДАННЫХ СПОРТИВНОЙ МЕДИЦИНЫ НА КОМПЬЮТЕРЕ

Критерий Хи-квадрат Пирсона используется для проверки гипотезы о нормальности закона распределения исследуемой случайной величины.

Для проверки гипотезы о том, что исследуемая случайная величина x подчиняется нормальному закону распределения F(x), необходимо произвести выборку из n независимых наблюдений и по ней построить эмпирический закон распределения F (x) . Для сравнения эмпирического F (x) и гипотетического F(x) законов

используется правило, называемое критерием согласия Пирсона, для которого вычисляется статистика Хи-квадрат (11):

где N – число интервалов, по которому строился эмпирический закон распределения; i – номер интервала; pit – вероятность попадания значения случайной величины в i-й интервал для теоретического закона распределения; pie – вероятность попадания значения случайной величины в i-й интервал для эмпирического закона распределения.

Если вычисленное значение статистики 2 превосходит квантиль распределения Хи-квадрат с k = n – p – 1 степенями свободы для заданного уровня значимости α, то гипотеза нормальности распределения отвергается. В противном случае эта гипотеза принимается на заданном уровне значимости α. Здесь n –

число наблюдений; p – число оцениваемых параметров закона распределения.

В приложении Г представлена таблица, содержащая значения χ2 распределения Пирсона для уровней значимости α =0,01 и α = 0,05.

Пример. Проверить нормальность распределения показателей из предыдущего примера (таблица 1.2). Поскольку выборка имеет объем n > 30 (n = 90), то в этой ситуации можно использовать критерий Хи-квадрат Пирсона.

Алгоритм решения [6]:

1Выдвигаем статистические гипотезы:

– нулевую – об отсутствии отличий;

– альтернативную – о наличии отличий.

2Создадим новую таблицу вкладка New (Главная) – группа File (Файл) – команда New (Создать) – вкладка Spreadsheed (Таблица). Введем данные в столбец, соответствующий переменной Var 1 (таблица 1.2).

3Запускаем модуль Distribution Fitting (Подгонка распределения): вкладка Statistics (Анализ) – группа Base (Базовая статистика) – Distribution Fitting

(Подгонка распределений). В окне модуля Distribution Fitting (Подгонка рас-

пределений) во вкладке Quick (Быстрый) (рисунок 1.21) выберем группу Continuous Distributions (Непрерывное распределение) и нажмем на кнопку OK. Да-

лее в появившемся окне Fitting Continuous Distributions (Подгонка непрерыв-

ного распределения) (рисунок 1.22) выберем переменную Var 1, нажимая на кнопку Variable (Переменная), и нажмем кнопку Plot of observed and expected distribution (График наблюдаемого и ожидаемого распределения).

31

Рисунок 1.21 – Окно Distribution Fitting

Рисунок 1.22 – Окно Fitting Continuous Distributions

4 Получаем гистограмму (рисунок 1.23), в еѐ окне значение статистики критерия χ2 = 6,111 при р < 0,190 и степени свободы k = 4. Расчетное значение критерия χ2расч меньше табличного значения χ2табл = 9,488 для k = 4 и α = 0,05. Следовательно нулевая гипотеза о нормальном распределении принимается при уровне значимости α = 0,05.

32

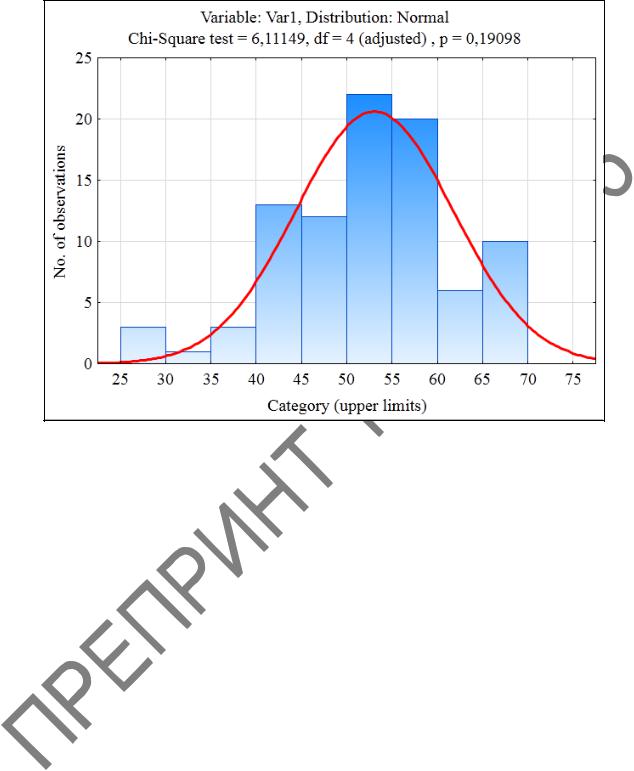
Рисунок 1.23 – Гистограмма для переменной Var 1

Замечание. При проверке гипотезы нужно внимательно проанализировать данные на наличие выбросов, иначе нулевая гипотеза может быть отвергнута ошибочно [3].

1.7 Варианты заданий по вычислению описательных статистик выбо-

рок в пакете STATISTICA 10

Для вариантов заданий провести следующий анализ:

1 Рассчитать следующие основные описательные статистики выборок: среднее значение, размах, выборочную дисперсию, выборочное стандартное отклонение, стандартную ошибку среднего, выборочный коэффициент асимметрии, выборочный коэффициент эксцесса, доверительный интервал для среднего с вероятностью 95 и 99%. Сделать выводы о выборке.

2 Построить гистограмму.

3 Проверить гипотезы нормальности распределения выборки по критериям Шапиро–Уилка, Колмогорова–Смирнова и Хи-квадрат Пирсона.

Вариант 1. Результаты бега на 100 м спринтера в соревновательном перио-

де, с: 10,8; 10,7; 10,7; 10,9; 10,6; 10,8; 10,7; 10,9; 10,8; 10,6 [7].

33

Вариант 2. Результаты измерения простой двигательной реакции у боксе-

ров, с: 0,16; 0,19; 0,13; 0,21; 0,18; 0,19; 0,10; 0,15; 0,20; 0,17 [7].

Вариант 3. Результаты прыжка на лыжах с трамплина квалифицированного лыжника, м: 91,5; 93; 89,5; 93; 90; 92; 95; 90,5; 92; 93,5; 93 [7].

Вариант 4. Результаты соревнований в прыжках в длину одного спортсме-

на, м: 8,07; 7,83; 7,77; 7,92; 7,75; 7,89; 7,95; 7,71; 8,00; 7,86 [7].

Вариант 5. Результаты выступления на соревнованиях пловца на 25 м кро-

лем, с: 25,3; 24,5; 24,3; 24,7; 24,0; 25,1; 24,6; 23,9; 24,1; 24,5 [7].

Вариант 6. Результаты прыжка в длину с места одного испытуемого, см: 257; 262; 245; 253; 267; 258; 253; 246; 260; 256; 261; 249 [7].

Вариант 7. Продолжительность кардиоинтервалов (то есть времени между сокращениями сердца) у спортсмена в покое составила, с: 0,97; 1,03; 1,07; 1,01; 0,95; 0,94; 0,99; 1,00; 1,12; 1,03 [7].

Вариант 8. Результаты бега на коньках на 500 м у спортсмена в соревнова-

тельном периоде, с: 41,4; 41,9; 41,0; 40,9; 41,6; 40,7; 40,3; 41,2; 42,1; 40,8 [7].

Вариант 9. Результаты выступления на соревнованиях по толканию ядра одного спортсмена, м: 15,00; 15,48; 14,93; 15,36; 15,00; 15,12; 15,24; 14,64; 14,88 [7].

Вариант 10. Результаты выступления пловца в плавании на 100 м брас-

сом, с: 69,7; 70,3; 68,9; 69,4; 68,8; 68,5; 69,0; 68,8; 70,4; 69,5 [7].

Вариант 11. Результаты измерения времени простой двигательной реакции бегуна-спринтера, с: 0,17; 0,13; 0,14; 0,11; 0,16; 0,15; 0,13; 0,14; 0,18; 0,15 [7].

Вариант 12. Результаты повторных измерений концентрации гемоглобина в крови пловца, мг %: 13,0; 13,9; 15,0; 15,1; 14,6; 14,7; 14,3; 14,6; 14,4; 14,5 [7].

Вариант 13. Результаты повторных измерений кистевой динамометрии бор-

ца, кг: 65; 67; 63; 64; 69; 70; 64; 63; 68; 64; 68; 61; 62 [7].

Вариант 14. Результаты повторных измерений результатов бега на 30 м с хода у бегуна-спринтера, с: 2,74; 2,86; 2,75; 2,77; 2,69; 2,73; 2,78; 2,83; 2,80 [7].

Вариант 15. Результаты повторных измерений времени реакции на движу-

щийся объект у вратаря, с: 0,38; 0,45; 0,59; 0,43; 0,49; 0,48; 0,42; 0,51; 0,50; 0,46 [7].

Вариант 16. Результаты повторного метания мяча школьником, м: 33,5; 35; 34,5; 36; 34,5; 34; 34,5; 33 [7].

Вариант 17. Результаты выступления в серии соревнований бегуна на 400 м,

с: 47,3; 47,8; 47,5; 47,1; 47,9; 48,4; 47,5; 46,9; 47,7; 48,3 [7].

Вариант 18. Результаты измерения повторных прыжков вверх с места во-

лейболиста, см: 92; 97; 95; 90; 99; 96; 103; 94; 96; 97; 93; 98; 91; 89 [7].

Вариант 19. Результаты выступления в серии соревнований прыгуна в вы-

соту, см: 219; 216; 232; 223; 225; 219; 214; 220; 222; 214; 216 [7].

Вариант 20. Результаты повторных измерений частоты сердечных сокращений у спортсмена в состоянии покоя, уд/мин: 53; 57; 58; 54; 52; 51; 53; 56; 55; 54; 54; 53; 52; 50; 54; 55 [7].

34

Вариант 21. Результаты выступления в серии соревнований прыгуна с шес-

том, м: 5,20; 5,35; 5,15; 5,40; 5,25; 5,30; 5,35; 5,45; 5,25; 5,20 [7].

Вариант 22. Результаты повторных измерений частоты беговых шагов спринтера: 4,87; 4,92; 6,07; 4,91; 4,88; 4,93; 4,92; 5,00; 4,93; 4,85 [7].

Вариант 23. Результаты повторных измерений времени одиночного удара боксера: 0,23; 0,19; 0,20; 0,24; 0,19; 0,22; 0,18; 0,23; 0,25; 0,22 [7].

Вариант 24. Результаты повторных измерений силы мышц разгибателей стопы, кг: 103,8; 105,3; 100,4; 107,3; 106,7; 104,9; 103,8; 105,0; 104,7 [7].

Вариант 25. Результаты повторных измерений становой динамометрии штангиста, кг: 209; 220; 215; 207; 212; 218; 226; 223; 215; 219; 206; 216 [7].

35

2 КЛАСТЕРНЫЙ АНАЛИЗ ДАННЫХ

2.1 Постановка задачи кластерного анализа

Кластеризация – это группировка наблюдений на основе данных, описывающих свойства наблюдений. Наблюдения внутри кластера должны быть похожими друг на друга и отличаться от других, которые вошли в другие кластеры.

Термин «кластер» переводится как гроздь, пучок. Все наблюдения, входящие в данный кластер, более схожи между собой, чем с элементами других кластеров. Таким образом, кластеризация помогает провести классификацию объектов (наблюдений). Этот метод анализа не использует априорных предположений о характере распределения и опирается только на сами данные [3].

Например, тренеры ставят задачу выявления и отбора талантливых спортсменов; медики проводят кластеризацию заболеваний, лечения заболеваний или симптомов заболеваний; биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними.

Кластеризацию используют, когда отсутствуют априорные сведения относительно классов, к которым можно отнести объекты исследуемого набора данных, либо когда число объектов велико, что затрудняет их ручной анализ [8].

Постановка задачи кластеризации сложна и неоднозначна, поскольку [8]:

1)оптимальное количество кластеров в общем случае неизвестно;

2)выбор меры «похожести» или близости свойств объектов между собой, как и критерия качества кластеризации, часто носит субъективный характер.

Цели кластеризации зависят от конкретной решаемой задачи и могут быть следующими [8]:

1 Изучение данных. Разбиение множества наблюдений на группы помогает выявить внутренние закономерности, увеличить наглядность представления данных, выдвинуть новые гипотезы, понять, насколько информативны свойства объектов.

2 Облегчение анализа. При помощи кластеризации можно упростить дальнейшую обработку данных и построение моделей: каждый кластер обрабатывается индивидуально, и модель создается для каждого кластера в отдельности. В этом смысле кластеризация может рассматриваться в качестве подготовительного этапа перед решением задач классификации и регрессии.

3 Сжатие данных. В случае, когда данные имеют большой объем, кластеризация позволяет сократить объем хранимых данных, оставив по одному наиболее типичному представителю от каждого кластера.

4 Прогнозирование. Кластеры используются не только для компактного представления объектов, но и для распознавания новых. Каждое новое наблюдение относится к тому кластеру, присоединение к которому наилучшим образом удовлетворяет критерию качества кластеризации. Значит, можно прогнозировать

36

поведение объекта, к которому относится наблюдение, предположив, что оно будет схожим с поведением других объектов кластера.

5 Обнаружение аномалий. Кластеризация применяется для выделения нетипичных наблюдений. Эту задачу также называют обнаружением аномалий. Интерес здесь представляют кластеры, в которые попадает крайне мало, например 1–3, наблюдений.

При кластеризации в классическом виде идет одновременная кластеризация и объектов наблюдения (например, спортсменов или пациентов), и признаков (например, спортивных показателей или симптомов). Однако на практике выбирают что-то одно. Выборка эмпирических данных в многомерном пространстве представлена набором точек двумя различными способами [3]:

1)набор точек – как объекты (наблюдения);

2)набор точек – как признаки.

Исследователь решает, что ему важнее. Многомерное пространство для осуществления кластеризации нужно превратить в метрическое, указав способ оп-

ределения расстояния (метрики) между его точками.

В определениях кластеризации встречается словосочетание «похожесть свойств». Термины «похожесть», «близость» можно понимать по-разному, поэтому в зависимости от выбора варианта оценки близости между свойствами объектов получается тот или иной вариант кластеризации [8].

2.2 Меры расстояний в кластерном анализе

Метрическое пространство – набор элементов, между которыми задана функция расстояния, называемая метрикой. Наиболее популярные метрики –

Евклидово расстояние, расстояние Манхэттена, расстояние Чебышева и степенное расстояние [8].

Евклидово расстояние вычисляется следующим образом (12):

X = (x1, х2, ..., xm), Y = (у1, у2, ..., ут) – векторы значений признаков двух наблюдений. Поскольку множество точек, равноудаленных от некоторого центра, при использовании Евклидовой метрики будет образовывать сферу (или круг в двумерном случае), кластеры, полученные с использованием Евклидова расстояния, так-

же будут иметь форму, близкую к сферической [8].

37

Расстояние Манхэттена (расстояние городских кварталов) вычисляется по следующей формуле (13):

X = (x1, х2, ..., xm), Y = (у1, у2, ..., ут) – векторы значений признаков двух наблюдений. Фактически расстояние Манхеттена – это кратчайшее расстояние между двумя точками, пройденное по линиям, параллельным осям прямоугольной системы координат. Само название «расстояние Манхеттена» возникло из-за ассоциаций, возникающих с прямоугольными формами застройки, которая характерна для

современных городов [8].

Преимущество расстояния Манхэттена заключается в том, что использование прямоугольной системы координат позволяет снизить влияние аномальных значений на работу алгоритмов кластеризации. Кластеры, построенные на основе расстояния Манхэттена, стремятся к кубической форме.

Расстояние Чебышева вычисляется по следующей формуле (14):

X = (x1, х2, ..., xm), Y = (у1, у2, ..., ут) – векторы значений признаков двух наблюдений. Расстояние Чебышева является максимумом модуля разности координат соответствующих признаков объектов. Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по

какой-либо одной координате (каким-либо одним измерением) [3]. Степенное расстояние вычисляется по следующей формуле (15):

X = (x1, х2, ..., xm), Y = (у1, у2, ..., ут) – векторы значений признаков двух наблюдений. Степенное расстояние является корнем р-степени из суммы степеней модулей разности координат соответствующих признаков объектов. Обобщенное сте-

пенное расстояние представляет только математический интерес в качестве универсальной метрики, поскольку при р = 2 получаем Евклидово расстояние, а при р = 1 – расстояние Манхеттена.

2.3 Этапы и алгоритмы кластерного анализа

Согласно [6] можно выделить следующие этапы проведения кластерного анализа:

1 Получение с помощью конкретных измерительных шкал выборки эмпирических данных, представление еѐ в виде таблицы «наблюдение–признак».

2 Определение направления кластеризации: спортсмены, пациенты, респонденты, наблюдения, измеренные признаки, или и то и другое одновременно.

38

3 Распределение эмпирических данных в виде точек многомерного метрического пространства с определенными координатами; определение меры сходства или различия между его точками.

4 Выбор основного принципа разделения выборки на кластеры.

5 Выбор конкретного алгоритма кластеризации с характерным приемом определения мер сходства или различия между кластерами, то есть способа определения межкластерных расстояний, и, естественно, способа оценки качества кластеризации.

6 Выполнение кластеризации или разбиения исходной выборки на кластеры. 7 Интерпретация результатов кластеризации.

Алгоритмы кластеризации делятся на агломеративные (объединительные) и дивизивные (разделительные). В первом случае мелкие кластеры объединяются в более крупные, а во втором случае – один крупный дробится на более мелкие. Оба эти процесса проводят до тех пор, пока не получат оптимальное число кластеров. Максимальное количество кластеров не должно превосходить количества элементов в выборке [3].

В пакете STATISTICA 10 реализовано три базовых метода кластерного анализа (рисунок 2.1) [3]:

1)агломеративный – объединение, или дерево кластеризации (Joining (tree clustering));

2)дивизивный – кластеризация k-средними (K-means clustering);

3)агломеративный – двунаправленное объединение и по наблюдениям и по переменным (Two-way joining).

Рисунок 2.1 – Методы кластеризации в пакете Statistica 10

39

2.4 Алгоритм кластеризации k-средних

Одной из широко используемых методик кластеризации является дивизионная кластеризация, в соответствии с которой для выборки данных, содержащей n наблюдений (объектов), задается число кластеров k, которое должно быть сформировано. Затем алгоритм разбивает все объекты выборки на k групп (k < n), которые и представляют собой кластеры [8].

К наиболее простым и эффективным алгоритмам дивизионной кластеризации относится k-средних (в англоязычном варианте k-means). Алгоритм k-средних состоит из следующих четырех шагов [8]:

1 Задается число кластеров k, которое должно быть сформировано из наблюдений исходной выборки.

2 Случайным образом выбирается k наблюдений, которые будут служить начальными центрами кластеров. Начальные точки, из которых потом вырастает кластер, часто называют «семенами». Каждое такое наблюдение представляет собой своего рода «семя» кластера, состоящее только из одного элемента.

3 Для каждого наблюдения исходной выборки определяется ближайший к ней центр кластера.

4 Производится вычисление центроидов – центров тяжести кластеров. Это делается путем определения среднего для значений каждого признака всех записей в кластере. Например, если в кластер вошли три записи с наборами признаков (x1, y1), (x2, y2), (x3, y3), то координаты его центроида будут рассчитываться следующим образом (16):

Затем старый центр кластера смещается в его центроид. Таким образом центоиды становятся новыми центрами кластеров для следующей итерации алгоритма.

Шаги 3 и 4 повторяются до тех нор, пока выполнение алгоритма не будет прервано либо пока не будет выполнено условие в соответствии с некоторым критерием сходимости.

Остановка алгоритма производится, когда границы кластеров и расположение центроидов перестают изменяться, то есть на каждой итерации в каждом кластере остается один и тот же набор наблюдений. Алгоритм k-средних обычно находит набор стабильных кластеров за несколько десятков итераций.

В качестве критерия сходимости чаще всего используется сумма квадратов ошибок между центроидом кластера и всеми вошедшими в него наблюдениями (17):