01 КАСЮК С. Т. ПЕРВИЧНЫЙ, КЛАСТЕРНЫЙ, РЕГРЕССИОННЫЙ И ДИСКРИМИНАНТНЫЙ АНАЛИЗ ДАННЫХ СПОРТИВНОЙ МЕДИЦИНЫ НА КОМПЬЮТЕРЕ

Вариант 2. Имеются результаты измерения спортивных показателей X1, X2, X3 мужчин-спортсменов в количестве 48 человек (таблица 2.7).

Таблица 2.7 – Вариант 2

Вариант 3. Имеются результаты измерения спортивных показателей X1, X2, X3, X4 женщин-спортсменок в количестве 40 человек (таблица 2.8).

Таблица 2.8 – Вариант 3

Вариант 4. Имеются результаты измерения спортивных показателей X1, X2, 62

X3 мужчин-спортсменов в количестве 40 человек (таблица 2.9).

Таблица 2.9 – Вариант 4

Вариант 5. Имеются результаты измерения спортивных показателей X1, X2, 63

X3, X4 мужчин-спортсменов в количестве 45 человек (таблица 2.10).

Таблица 2.10 – Вариант 5

3.1 Постановка задачи регрессионного анализа

Существует большой класс задач, для которых требуется установить зависимость между признаками (атрибутами, показателями), которые описывают исследуемый процесс или объект предметной области. Для этого строятся различные модели, в которых данные признаки выступают в качестве переменных. Если модель будет корректно отражать зависимость между входными и выходными переменными, то с помощью такой модели можно будет предсказывать значения выходной переменной по заданным значениям входных [8].

Как правило, реальные процессы в спортивной медицине и спорте достаточно сложны, и для их описания требуется большое количество переменных, которое может насчитывать и несколько десятков в зависимости от сложности объекта исследования.

Рассмотрим простой пример. В таблице 3.1 представлены лучшие результаты в беге на 100 м и по прыжкам в длину спортсменов различной квалификации. Выявим зависимость в данных с помощью линейной регрессии.

Таблица 3.1 –Результаты спортсменов различной квалификации

Цель анализа – оценка ожидаемых результатов прыжка в длину, м, в зависимости от времени бега, с, на дистанции 100 м.

Если предположить, что зависимость между переменными линейная, то для построения модели достаточно провести прямую линию, проходящую через «облако» точек, соответствующих наблюдениям (рисунок 3.1). Тогда наклон линии покажет, насколько уменьшится результат при увеличении времени.

Если мы хотим смоделировать зависимость прыжка в длину в метрах от времени бега на дистанцию 100 метров, то нужно построить прямую, каждая точка которой будет представлять собой оценку прыжка в длину для заданного времени бега. Однако таких линий можно построить бесконечно много, и только одна из них обеспечит оптимальную оценку прыжка в длину. Естественным было бы провести линию таким образом, чтобы рассеяние вдоль нее точек, соответствующих реальным наблюдениям, было минимальным.

65

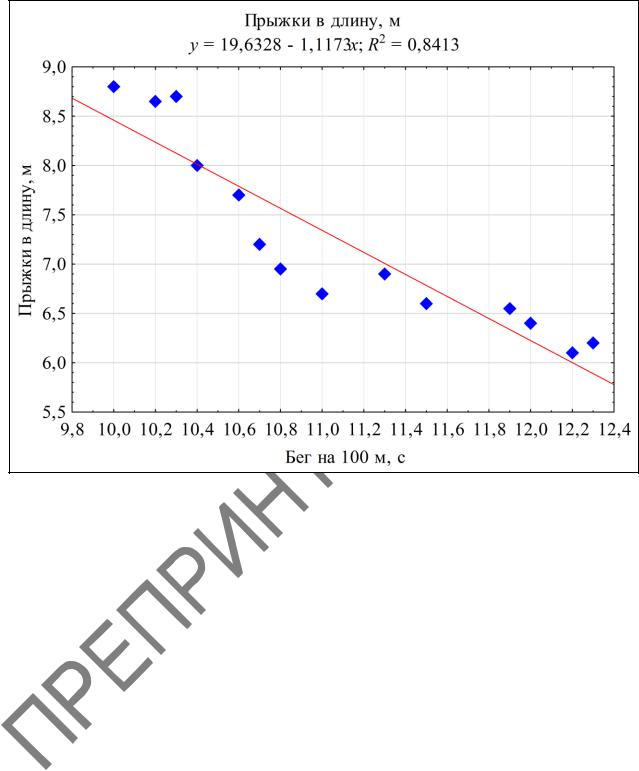
Рисунок 3.1

На практике линию строят так, чтобы сумма квадратов отклонений наблюдаемых значений от оцененных с помощью данной линейной зависимости была минимальной, то есть (22):

i 1

где n – число наблюдений; yˆi – оценка выходного значения i-го наблюдения,

полученная с помощью модели; yi – реально наблюдаемое значение в i-м наблюдении [8].

Данный метод известен как метод наименьших квадратов (МНК), а линия построенная с его помощью, называется линией регрессии.

Линия регрессии – это прямая наилучшего приближения для набора пар значений входной и выходной переменной (х, у), выбираемая таким образом, чтобы сумма квадратов расстояний от точек (хi, yi) до этой прямой, измеренных вертикально (то есть вдоль оси у), была минимальна.

66

Уравнение, описывающее линию регрессии, называется уравнением

где yˆ – оценка значения выходной переменной; b0 – точка пересечения линии с осью у, называемая также свободным членом. Это значение, которое принимает выходная переменная yˆ при х = 0. Коэффициент b1 определяет наклон линии

относительно оси х.

Коэффициенты линейного уравнения b0 и b1 называются коэффициентами регрессии.

Таким образом, задача построения модели простой линейной регрессии сводится к нахождению таких коэффициентов b0 и b1 для которых сумма квадратов ошибок, то есть разностей между реально наблюдаемыми значениями выходной

где ε – ошибка.

Тогда сумму квадратов ошибок по всем наблюдениям можно вычислить следующим образом (25):

Мы можем найти значения b0 и которые минимизируют путем дифференцирования уравнения (23) по b0 и b1. Частные производные для уравнения (25) по b0 и b1 соответственно будут (26):

Как известно, в точке, где функция минимальна, ее производная обращается в ноль. Поэтому нас интересуют значения b0 и b1 которые обращают (25) в ноль, то есть (27):

Опустив некоторые промежуточные выкладки, сразу запишем результат (28):

где n – общее число наблюдений; yср – среднее значение выходной переменной; хср – среднее значение входной переменной [8].

67

Уравнения (28) – это полученные методом МНК для значений b0 и b1 оценки, которые минимизируют сумму квадратов ошибок.

Разности между наблюдаемыми значениями выходной переменной и значениями, оцененными с помощью регрессии, называются остатками. Справедливо:

наблюдение = оценка + остаток.

Используя МНК, вычислим оценки коэффициентов регрессии для данных из таблицы 3.1: b1 = 19,63; b0 = –1,12.

Уравнение регрессии будет иметь следующий вид: yˆi = 19,63 – 1,12x.

Смысл коэффициентов уравнения регрессии следующий: b0 – это значение выходной переменной у при значении входной переменной х = 0. Значит, если бы спортсмен пробежал дистанцию 100 метров за 0 секунд, то оценка его прыжка в длину составила бы 19,63 метра. Однако данная формальная интерпретация явно противоречит здравому смыслу, поскольку спортсмен не может бежать бесконечно быстро. Отсюда вытекает одно из ограничений линейной регрессии: линию регрессии следует считать подходящей аппроксимацией некоторой реальной функции только в том диапазоне изменений входной переменной х, в котором распределены исходные наблюдения. В противном случае результаты могут оказаться непредсказуемым [8].

Значение коэффициента наклона линии регрессии b1 можно интерпретировать как среднюю величину изменения значения выходной переменной при изменении значения входной переменной на единицу. В нашем примере это означает, что при увеличении результата в беге на одну секунду можно ожидать увеличения расстояния прыжка в среднем на 1,12 метра.

Линия регрессии для найденного нами уравнения представлена на рисунке 3.1. Для линии регрессии сумма квадратов вертикальных расстояний между точками данных и линией должна быть меньше, чем аналогичная сумма квадратов для любой другой прямой.

3.2 Линейная регрессионная модель

Простая линейная регрессионная модель задается следующим образом [8]. Пусть имеется выборка данных, содержащая n наблюдений, в каждом из которых значению независимой переменной хi соответствует значение зависимой переменной yi связанных с помощью линейной зависимости:

у = b0 + b1 x + ε,

где b0 и b1 – параметры модели, определяющие точку пересечения линии регрессии с осью у и наклон линии регрессии соответственно; ε – остатки, определяющие ошибку отклонения реального наблюдения от оценки, полученной с помощью данной модели.

68

В общем случае линейные регрессионные модели с несколькими независи-

1)остатки ε является случайной величиной с нулевым средним значением;

2)дисперсия остатков ε является постоянной величиной;

3)отдельные значения остатков ε являются независимыми;

4)остатки ε является нормально распределенной случайной переменной.

3.3 Оценка соответствия простой линейной регрессии реальным данным

Линия регрессии должна аппроксимировать линейные отношения между входной и выходной переменными модели. Однако при этом возникает вопрос, насколько линейная аппроксимация соответствует наблюдаемым данным. Чтобы определить это, введем в рассмотрение два показателя – стандартную ошибку

В статистике мерой разброса случайной величины относительно среднего значения является стандартное отклонение. Аналогично в качестве меры разброса точек наблюдений относительно линии регрессии можно использовать стандартную ошибку оценивания, которая показывает среднюю величину отклонения точек исходных данных от линии регрессии вдоль оси у. Стандартная ошибка равна корню квадратному среднеквадратической ошибки (СКО) [8], которая определяется как сумма квадратов разностей между реальным и оцененным значениями, вычисленной по всем наблюдениям и отнесенной к их числу (30):

СКО можно рассматривать как меру изменчивости выходной переменной, объясняемую регрессией. Тогда стандартная ошибка оценивания определяется следующим образом (31):

рассогласования оценок, полученных с помощью регрессии, и реальных наблюдений аналогично тому, как стандартное отклонение позволяет оценить в статистическом анализе степень разброса случайной величины относительно среднего. Чем меньше стандартная ошибка оценивания, тем лучше работает модель.

69

Рассмотрим пример из литературы [8]. Имеется выборка, в которой представлены данные, описывающие результаты соревнований по спортивному ориентированию: расстояние в километрах, пройденное десятью участниками за определенное время, выраженное в часах. На основе наблюдений за участниками соревнований было получено уравнение регрессии у = 6 + 2х. Пройденное расстояние определяется как 6 км плюс удвоенное количество часов, затраченных на движение. Уравнение позволяет оценить расстояние, пройденное за произвольное количество часов. Полученные оценки представлены в таблице 3.2.

Таблица 3.2 – Расчет СКО для примера о спортивном соревновании

ния значения выходной переменной с помощью данного уравнения регрессии. Если она велика, то модель работает неудовлетворительно. Является ли значение, равное 12, большим? Достоверно сказать нельзя, поскольку на данном этапе мы не имеем других мер для сравнения.

Стандартная ошибка будет ˆ =1,1. Следовательно, при оценке

Ест 12 10

пути, пройденного участником соревнований, с помощью уравнения yˆ = 6 + 2х

ожидаемая ошибка равна 1,1 км.

Теперь предположим, что информация о количестве часов, которое каждый участник соревнований провел в пути, отсутствует, то есть использовать переменную х для оценивания переменной у невозможно. Полученные в этом случае оценки пройденного расстояния окажутся менее точными, поскольку количество исходной информации уменьшится. Тогда единственно возможной оценкой для у

70