
- •Алгебра және геометрия
- •Комплекс санның алгебралық түрі, қолданылатын амалдар мен қасиеттері. Жазықтықта кескіндеу және тригонометриялық түрі. Муавр формуласы. Комплекс саннан n-дәрежелі түбір табу формуласы.
- •1. Комплекс санның алгебралық түрі, қолданылатын амалдар мен қасиеттері. Жазықтықта кескіндеу және тригонометриялық түрі. Муавр формуласы. Комплекс саннан n-дәрежелі түбір табу формуласы.
- •2. Векторлық кеңістіктің аксиомалары. Векторлар жүйесінің сызықты тәуелділігі мен тәуелсіздігі. Сызықтық тәуелділіктің қасиеттері.
- •3. Көпмүшеліктердің бөлінгіштік қасиеттері. Көпмүшеліктердің ең үлкен ортақ бөлгіші. Ең үлкен ортақ бөлгішті табудың Евклид алгоритмі.
- •4. Кері матрица. Матрицаның керілену критерийі.
- •5. Векторлардың векторлық және аралас көбейтінділері және олардың геометриялық мағынасы.
- •3 Вектордың аралас көбейтіндісі
- •6. Жазықтықтағы түзудің теңдеулерінің түрлері. Нүктеден түзуге дейінгі арақашықтық. Жазықтықтағы екі түзудің арасындағы бұрыш.
- •7. Жазықтықтың теңдеулерінің түрлері. Нүктеден жазықтыққа дейінгі арақашықтық. Екі жазықтықтың арасындағы бұрыш.
- •8. Екінші ретті қисықтардың канондық теңдеулері. Эллипс пен гиперболаның эксцентриситеттері мен директрисалары.
7. Жазықтықтың теңдеулерінің түрлері. Нүктеден жазықтыққа дейінгі арақашықтық. Екі жазықтықтың арасындағы бұрыш.
Жазықтықтың теңдеулерінің түрлері
Жазықтықта жататын кез-келген 2 коллиниар емес вектор оның бағыттауыш векторлары деп аталады. Жазықтықтың теңдеуін жазу үшін 3 нәрсе к/к.: 1нүкте ж/е 2 бағыттауыш вектор.

![]()
![]() жазықтық
жазықтық

![]()
![]() ,
бағыттауыш вектор
,
бағыттауыш вектор
![]() ,бағыттауыш
вектор,
,бағыттауыш
вектор,
![]() ,
параллель емес векторлар
,
параллель емес векторлар
![]() -
ағымдағы нүкте
-
ағымдағы нүкте
![]() -
-![]() =
=![]()
(![]() ,
,
![]() )-
базис
)-
базис
![]() ;
;
![]()
![]() -
-![]()
![]() =
=![]() - жазықтықтың векторлық, параметрлік
теңдеуі
- жазықтықтың векторлық, параметрлік
теңдеуі
![]()
![]()
![]()
![]()
![]()
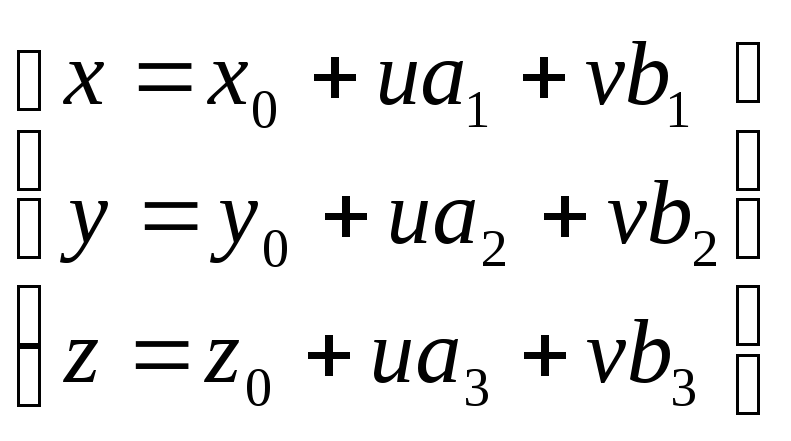 (2)
жазықтықтың
координаттық, параметр-к теңдеуі.
(2)
жазықтықтың
координаттық, параметр-к теңдеуі.
![]() компланар
векторлар болуы қажетті және жеткілікті
компланар
векторлар болуы қажетті және жеткілікті
(![]() ,
,
![]() )=0
)=0
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =0
(3)
=0
(3)
![]()
![]()
![]()
Жазықтықтың жалпы теңдеуі
Теорема: 1) Аффин координат-р жүйесінде кез-келген жазықтықтың теңдеуі кеңістікте бірнеше дәрежелі теңдеумен жазылады.
![]() (4)
(4)
2) Кез келген (4) түрдегі теңдеу кеңістікте жазықтықты анықтайды.
Д/у: 1)дәлелдеу үшін (3) пен (4) тің байланысын табу керек.
(3) =>(4) (3)ті 1-қатар бойынша жіктейміз.
![]()






![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =0
=0
=А =В =С
![]() => Ax+By+Cz+D=0;
=> Ax+By+Cz+D=0;
2)
(4)=>(3) (4)
![]() => ал (4) 1 дербес.
=> ал (4) 1 дербес.
Шешімі
![]() =>
=>
![]() (5).
(5).
(4)-(5)=
![]() (6)
(6)
![]()


![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() (7).
(7).
(6)=(7)=>(3) теорема дәлелденді.
Салдары 1. (4) түрлі теңдеу жазықтықтың жалпы теңдеуі д.а.
Салдары
2. (6) теңдеу
![]()
( 6)= (
6)= (![]() ,
,![]() )
= 0;
)
= 0;
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Декарт
координаттар жүйесінде
![]() (А,В,С)
– жазықтықтың нормаль векторы д.а.
(А,В,С)
– жазықтықтың нормаль векторы д.а.
Үш нүкте арқылы жазылған жазықтықтың теңдеуі.
![]()
![]() бір
түзудің бойында жатпайды.
бір
түзудің бойында жатпайды.

![]()


( 3)
3)
![]()
![]()
![]()
![]()
![]()
![]() = 0
(8)
= 0
(8)
![]()
![]()
![]()
Кесінділер арқылы берілген жазықтықтың теңдеуі
( 4)
4)![]() / -D
/ -D
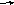

![]() (9)
(9)
![]() =
a;
=
a;
![]() =
b;
=
b;![]() =
c.
=
c.
1 )
x=0 y=0 z=c
)
x=0 y=0 z=c![]()
2 )
x=0 z=0 y=b
)
x=0 z=0 y=b![]()
3 )
y=0 z=0 x=a
)
y=0 z=0 x=a![]()

Екі жазықтықтың орналасуы және арасындағы бұрыш.
![]()
![]()
1 )
)![]()
2)
![]()
3)
![]()

Екі жазықтықтың арасындағы бұрыш –ол нормаль-р-ң арасындағы бұрыш.
![]()
 Нүктелердін
жазықтыққа дейінгі арақашықтығы.
Нүктелердін
жазықтыққа дейінгі арақашықтығы.
Ax+By+C+D=0;
 d-?
(арақашықтық)
d-?
(арақашықтық)
![]()
M(x,y,z)![]()
d=![]() =
= =
=
=
=![]()
8. Екінші ретті қисықтардың канондық теңдеулері. Эллипс пен гиперболаның эксцентриситеттері мен директрисалары.
Жоғары математикада екінші дәрежелі теңдеулермен анықталатын сызықтарды екінші pеттi қисықтар деп атайды. Олар негізінен шеңбер, эллипс, гипербола және парабола деп аталады. Бұл қисықтар техника мен ғылым саласында иі кездеседі.
1. Шеңбер. Шеңбердеп аталатын берілген нүктеден бірдей қашықтықта жататын жазықтықтағы нүктелердің геометриялық орындарын шенбер деп атайды.
С(х0,у0) - берілген нукте. Шеңбердің бойынан кез келген
жылжымалы М(х,у) нүктесін алайык. Сонда СМ(х -х0,у-у0),

мұндағы
F1
және
F2
-фокус
деп
аталатын
берілген
![]() центрі
С
нуктесінде
жаткан
радиусы
R
-ге
тең
шеңбердің
канондық
теңдеуі.
центрі
С
нуктесінде
жаткан
радиусы
R
-ге
тең
шеңбердің
канондық
теңдеуі.
Егер шеңбердің центрі С координаттардың бас нүктесінде жатса, онда х0 = у0 = 0 .
Сондықтан: х2 +у2 = R2
2. Эллипс. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы әрқашанда тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды. Анықтама бойынша F1M + F2M = 2a
нүктелер,

2а-тұрақты шама
Егер F1F2 = 2с десек, онда F1(-C;0), F2(C;0). Сонда:

Енді осы мәндерді қойсақ:
![]()
немесе
![]()

Егер а>с болса, онда а2 —с2=b2 болады. Сондықтан эллипстің канондық теңдеуі деп аталатын теңдеуге келеміз:
![]()
Мұндағы х пен у эллипстің кез келген жылжымалы нүктесінің координаттары, а – эллипстің үлкен жарты oci, b – онын кіші жарты oci.
Осьтер эллипске симметриялы, ал симметриялы осьтердің қиылысатын нүктесі эллипстің цeнтpi болады.
![]() қатынасын
эллипстің эксцентриситеті
деп атайды және оны
қатынасын
эллипстің эксцентриситеті
деп атайды және оны
![]() деп
белгілейді. Сонымен 6ipгe а
> с болғандьқтан
l
< 1
немесе
деп
белгілейді. Сонымен 6ipгe а
> с болғандьқтан
l
< 1
немесе
![]()
Эллипстің
үлкен осіне перпендикуляр түзулердің
ішінде 6ip
түзудің
эллипстің кіші осінен қашықтықты d
әрқашанда
а/l
қатынасына тең тұрақты
шама болса, онда мұндай түзуді
эллипстің
директрисасы
деп атайды. Директрисалардың тендеу
![]() .
Эллипс
үшін l
< 1
болғандьқтан
.
Эллипс
үшін l
< 1
болғандьқтан
![]() .
.
Сондықтан эллипстің директрисалары оның сыртында жатады.
Егер a=b болса, онда шеңбер эллипстің дерпбес жағдайы болады. Бұл жағдайда с=0, ендеше шеңбердің эксцентриситеті нөлге тең.
3 .
Гипербола.
Фокустар
деп аталатын берілген екі
нүктеден
қашықтықтарының
айырмасы әрқашанда тұрақты шама
болатын
жазықтықтағы нүктелердің
геометриялық орындарын гипербола деп
атайды.
.
Гипербола.
Фокустар
деп аталатын берілген екі
нүктеден
қашықтықтарының
айырмасы әрқашанда тұрақты шама
болатын
жазықтықтағы нүктелердің
геометриялық орындарын гипербола деп
атайды.
4. Парабола. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын жазықтықтарды нүктелерің геометриялык орындарын парабола дейді Берілген F нүктесінің координаталарын былай белгілейді
Координаталардың бас нүктесінен Р/2 қашықтықтағы ординат осіне параллель берілген түзуді параболаның директрисасы дейді.
М(х,у) - параболаның бойындағы кез келген жылжымалы нүкте.
Анықтама бойынша
FM=ME
Екі нүктенің ара қашықтығыньң формуласы бойынша
![]()
осы мәндерді апарып қойып, шыққан өрнекті түрлендірсек, параболаның канондық теңдеуі шығады:
у2=2рх
мұндагы р -берілген фокус пен директрисаның арасындағы қашықтық, х пен у - параболаның бойындағы кез келген жылжымалы нуктенің координатасы.
Параболаның
эксцентриситеті:
![]()
Параболаның
директрисасының теңдеуі:
![]()
