
- •3. На практике координаты векторов удобно представлять в виде матриц-столбцов (или матриц-строк), которые называются координатными столбцами (координатными строками).
- •Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора.
- •Скалярное произведение векторов и его свойства
- •7.3. Выражение векторного произведения через координаты
- •Угол между векторами
- •Смешанное произведение векторов и его свойства
- •Уравнение прямой на плоскости
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
- •Угол между двумя прямыми.
- •Угол между двумя прямыми
- •Расстояние от точки до прямой на плоскости.
- •Задача: в кубе abcd a1b1c1d1 с ребром 2 точки m — середина ребра a1d1. Найти расстояние от точки c до плоскости ab1mГеометрический способ.
- •Пусть плоскости p1 и p2 в пдск Оxyz заданы уравнениями:
- •§19. Взаимное расположение прямых и плоскостей в пространстве.
- •Гипербола: определение, свойства, построение
- •§ 121. Исследование формы параболы.
- •§ 123. Касательная к параболе.
- •§ 124. Оптическое свойство параболы.
- •§ 125. Полярное уравнение эллипса, гиперболы и параболы.
- •§ 126. Эллипс, гипербола и парабола как конические сечения.
§19. Взаимное расположение прямых и плоскостей в пространстве.
1. Взаимное расположение двух плоскостей. Возьмем две плоскости, заданные в АСК общими уравнениями:
П1: А1х + В1у + C1z + D1 = 0 (*)
П2: А2х + В2у + C2z + D2 = 0 (**)
и попытаемся, используя только данные уравнения, установить взаимное расположение этих плоскостей. Подобную задачу мы уже решали для прямых на плоскости; результаты для плоскостей в пространстве оказываются аналогичными.
(19.1) Теорема. Плоскости П1 и П2 параллельны в широком смысле тогда и только тогда, когда коэффициенты при х, у и z в их общих уравнениях пропорциональны, т.е.
(19.2) существует такое действительное число k, что А2 = kA1, В2 = kВ1, С2 = kС1.
При условии (19.2) плоскости П1 и П2 совпадают тогда и только тогда, когда
(19.3) D2 = kD1.
ð
Параллельность плоскостей в широком
смысле означает, что всякий вектор,
параллельный одной из них, параллелен
и другой.[20] Пусть
выполнено условие (19.2). Тогда по признаку
параллельности вектора и плоскости
р(а,b,c) || П1 Û
A1a
+ B1b
+ C1c
= 0 Û k(A1a
+ B1b
+ C1c)
= 0 Û A2a
+ B2b
+ C2c
= 0 Û р(а,b,c) || П2.
Значит, условие (19.2) влечет параллельность
плоскостей. Обратно, пусть П1 ||
П2.
Не умаляя общности, будем считать, что
С1 ¹
0. Векторы a(0,–C1,
B1)
и b(–C1,0,A1),
параллельные П1,
параллельны и П2.
Отсюда по признаку параллельности
вектора и плоскости имеем: a || П2 Þ
–C1В2+B1С2 =
0 Þ ![]() В1 и
b || П2 Þ
–C1A2+A1С2 =
0 Þ
В1 и
b || П2 Þ
–C1A2+A1С2 =
0 Þ ![]() A1.
Учитывая, что С2 =
A1.
Учитывая, что С2 = ![]() С1,
получаем, что равенство (19.2) выполнено
при k =
С1,
получаем, что равенство (19.2) выполнено
при k = ![]() .
Признак параллельности доказан.
.
Признак параллельности доказан.
Признак совпадения плоскостей в одну сторону очевиден: если все коэффициенты уравнения (**) пропорциональны соответствующим коэффициентам уравнения (*), то эти уравнения равносильны. Обратно, если П1 = П2, то П1 || П2 и выполнено условие (19.2). Осталось взять произвольную точку М0(х0,у0,z0)ÎП1=П2, подставить ее координаты в уравнения (*) и (**) и заметить, что D2 = –(A2x0+B2y0+C2z0) = k(–A1x0–B1y0–C1z0) = kD1. ð
2. Прямая как пересечение двух плоскостей. Возьмем две непараллельные плоскости, заданные уравнениями (*) и (**) из п.1. Они пересекаются по прямой l, заданной системой
(19.4) 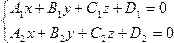 ,
,
которая называется системой общих уравнений прямой в пространстве. Очевидно, так можно задать любую прямую.
При решении задач на прямую, заданную общими уравнениями, бывает полезна
(19.5)
Теорема. Вектор р(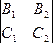 ,
,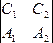 ,
, )
является направляющим для прямой,
заданной системой (19.4).
)
является направляющим для прямой,
заданной системой (19.4).
ð
Достаточно показать, что этот вектор
параллелен обеим плоскостям, заданным
уравнениями из системы (19.4). Применим
признак параллельности вектора и
плоскости: р || П1 Û
А1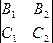 +
В1
+
В1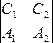 +
С1
+
С1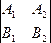 =
0 Û
=
0 Û 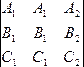 =
0. Но последнее равенство очевидно, ибо
у определителя в его левой части – два
одинаковых столбца. Аналогично проверяется
и условие р || П2.
ð
=
0. Но последнее равенство очевидно, ибо
у определителя в его левой части – два
одинаковых столбца. Аналогично проверяется
и условие р || П2.
ð
3. Взаимное расположение прямой и плоскости. Установим взаимное расположение прямой l = [М0(х0,y0,z0), р(a,b,c)] и плоскости П: Ax + By +Cz + D = 0. Признак их параллельности в широком смысле очевиден: l || П Û р || П Û
(19.6) Aa + Bb +Cc = 0
Теперь разберемся, когда прямая лежит в плоскости. Для этого необходимо и достаточно, чтобы прямая и плоскость были параллельны, и точка М0 лежала в плоскости. Задавая оба условия аналитически, получаем систему, составленную из равенства (19.6) и условия принадлежности точки М0 плоскости П:
(19.7) Ах0 + Ву0 + Сz0 + D = 0.
Наконец, прямая пересекает плоскость тогда и только тогда, когда не выполнено условие (19.6). Чтобы в этом случае найти точку пересечения, удобнее всего задать прямую l параметрическими уравнениями, подставить их в уравнение плоскости и найти соответствующее точке пересечения значение параметра.
4. Взаимное расположение двух прямых. (19.8) Лемма. Прямые l = [М0(х0,y0,z0), р(a,b,c)] и m = [M1(х1,y1,z1), q(a1,b1,c1)] лежат в одной плоскости тогда и только тогда, когда векторы M0M1, p и q компланарны, т.е.
(19.9) 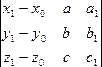 =
0 .
=
0 .
ð Пусть векторы M0M1, p и q компланарны. Это значит, что они параллельны некоторой плоскости a0. Проведем через точку М0 плоскость a || a0. Поскольку М0М1 || a, точка М1лежит в плоскости a. Кроме того, векторы p и q параллельны этой плоскости. Значит, прямые l и m лежат в ней. Обратно, пусть прямые l и m лежат в некоторой плоскости. Тогда векторы p и q параллельны ей, а точки M0 и M1 лежат в ней. Значит, вектор M0M1 тоже параллелен этой плоскости, что и завершает доказательство. ð
(19.10) Лемма. Прямые l и m совпадают тогда и только тогда, когда все три вектора M0M1, p и q коллинеарны.
ð То, что из совпадения прямых вытекает коллинеарность векторов, очевидно. Обратно, пусть векторы коллинеарны. Тогда прямая m и вектор M0M1 параллельны прямой l. Так как точка М0 лежит на этой прямой, на ней же лежит и точка М1. Значит, прямая m параллельна прямой l и имеет с ней общую точку, откуда l = m. ð
Теперь мы можем описать алгоритм выяснения взаимного расположения двух прямых. Сначала проверяем равенство (19.9). Если оно не выполнено, прямые скрещиваются. Если выполнено, проверяем коллинеарность векторов p и q. Если они не коллинеарны, прямые лежат в одной плоскости и не параллельны, т.е., они пересекаются. Если же p || q, проверяем, коллинеарны ли векторы M0M1 и p. Если да – прямые совпадают, если нет – параллельны в узком смысле.
Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми в пространстве. Расстояние между двумя срещивающимися прямыми.
Пусть прямые l1 и l2 относительно прямоугольной декартовой системы координат заданы своими каноническими уравнениями:
![]()
![]()
![]()
Возможны два случая :
1.
Прямые ![]() и
и![]() лежат
в одной плоскости.
лежат
в одной плоскости.
Прямые, находясь в одной плоскости, так же могут :
1.1. Совпадать
![]()
1.2. Быть параллельными
![]() не
параллельно
не
параллельно ![]()
1.3. Пересекаться
![]() не
параллельно
не
параллельно ![]()
![]() ,
, 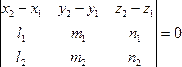 .
(1)
.
(1)
1.3.1
Условие перпендикулярности прямых: ![]()
2.
Прямые ![]() и
и![]() скрещиваются.
скрещиваются.
Если не выполняется условие 1.
Угол между двумя прямыми.
Пусть прямые l1 и l2 относительно прямоугольной декартовой системы координат заданы своими каноническими уравнениями:
![]()
![]()
![]()
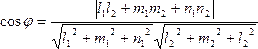
Расстояние между двумя срещивающимися прямыми.
d1 ![]() d2
d2 ![]() d1 и
d2 скрещивающиеся
прямые.
d1 и
d2 скрещивающиеся
прямые.
![]()
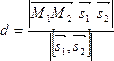
Условия параллельности и перпендикулярности двух прямых
Условие параллельности прямых заключается в равенстве их угловых коэффициентов.
tgφ1=tgφ2 или k1=k2
Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1
k1k2=-1
Пример 6. Проверить, выполняется ли условие параллельности прямых 2х-3у+1=0 и 4х-6у-5=0 ?
Решение:
Угловые коэффициенты этих прямых ![]() ,
т.е. условие параллельности выполнено.
,
т.е. условие параллельности выполнено.
Пример 7. Составить уравнение прямой линии, проходящей через точку (1;2) параллельно прямой 2х-3у+1=0.
Решение.
Угловой коэффициент k прямой линии, для
которой нужно составить уравнение,
равен угловому коэффициенту ![]() данной
прямой в силу условия параллельности
этих прямых. Таким образом,
данной
прямой в силу условия параллельности
этих прямых. Таким образом,![]() получим
искомое уравнение:
получим
искомое уравнение:![]() или,
умножая на 3: 3y-6=2(x-1), или 3y-6=2x-2, откуда
окончательно находим: 2x-3y+4=0
или,
умножая на 3: 3y-6=2(x-1), или 3y-6=2x-2, откуда
окончательно находим: 2x-3y+4=0
Пример 8. При каком значении k уравнение y=kx+1 определяет прямую, перпендикулярную к прямой у=2х-1?
Решение:
Угловой коэффициент второй прямой k2=2.
Условие перпендикулярности дает 2k=-1,
откуда ![]()
Пример 9. Составить уравнение прямой линии, проходящей через точку (-1;1) перпендикулярно к прямой 3х-у+2=0.
Решение:
Искомый угловой коэффициент обозначим
через k1,
угловой коэффициент данной прямой k2,
как видно из ее уравнения, равен 3. Условие
перпендикулярности k1k2=-1
нам дает: 3k1=-1,
откуда ![]() .
Таким образом, искомое уравнение
.
Таким образом, искомое уравнение![]() ,
или 3у-3=-х-1, и окончательно x+3y-2=0
,
или 3у-3=-х-1, и окончательно x+3y-2=0
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим
две плоскости α1 и
α2,
заданные соответственно уравнениями: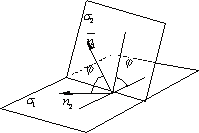
![]()
Под углом между
двумя плоскостями будем понимать один
из двугранных углов, образованных этими
плоскостями. Очевидно, что угол между
нормальными векторами ![]() и
и![]() плоскостей
α1 и
α2 равен
одному из указанных смежных двугранных
углов
плоскостей
α1 и
α2 равен
одному из указанных смежных двугранных
углов ![]() или
или![]() .
Поэтому
.
Поэтому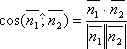 .
Т.к.
.
Т.к.![]() и
и![]() ,
то
,
то
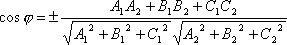 .
.
Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.
![]()
Условие параллельности двух плоскостей.
Две
плоскости α1 и
α2 параллельны
тогда и только тогда, когда их нормальные
векторы ![]() и
и![]() параллельны,
а значит
параллельны,
а значит![]() .
.
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
![]() или
или ![]()
Условие перпендикулярности плоскостей.
Ясно,
что две плоскости перпендикулярны тогда
и только тогда, когда их нормальные
векторы перпендикулярны, а
следовательно, ![]() или
или![]() .
.
Таким
образом, ![]() .
.
Примеры.
Составить уравнение плоскости, проходящей через точку
M(-2; 1; 4) параллельно плоскости 3x+2y-7z+8=0.
Уравнение
плоскости будем искать в виде Ax+By+Cz+D=0.
Из условия параллельности плоскостей
следует, что: ![]() .
Поэтому можно положитьA=3, B=2, C=-7.
Поэтому уравнение плоскости принимает
вид3x+2y-7z+D=0.
.
Поэтому можно положитьA=3, B=2, C=-7.
Поэтому уравнение плоскости принимает
вид3x+2y-7z+D=0.
Кроме того, так какMÎ α, то-6+2-28+D=0, D=32.
Итак, искомое уравнение 3x+2y-7z+32=0.
Составить уравнение плоскости, проходящей через точки M1(1; 1; 1), M2(0; 1; –1) перпендикулярно плоскости x+y+z=0.
Так как M1Î α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.
Далее, так как M2Î α, то подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.
Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.
Выразим коэффициенты Aи Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.
Окончательно получаем -2x+y+z=0.
Составить уравнение плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.
Так как MÎ α, то A(x+2)+B(x-3)+C(z-6)=0.
По
условию задачи ![]() ,
поэтому
,
поэтому
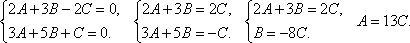
Итак уравнение плоскости принимает вид 13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.
ПРЯМАЯ В ПРОСТРАНСТВЕ.
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Положение
прямой в пространстве вполне определяется
заданием какой-либо её фиксированной
точки М1 и
вектора ![]() ,
параллельного этой прямой.
,
параллельного этой прямой.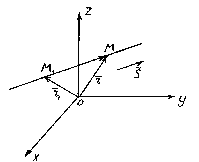
Вектор ![]() ,
параллельный прямой,
называетсянаправляющим вектором
этой прямой.
,
параллельный прямой,
называетсянаправляющим вектором
этой прямой.
Итак,
пусть прямая l проходит
через точку М1(x1, y1, z1),
лежащую на прямой параллельно вектору ![]() .
.
Рассмотрим
произвольную точку М(x,y,z) на
прямой. Из рисунка видно, что ![]() .
.
Векторы ![]() и
и![]() коллинеарны,
поэтому найдётся такое числоt,
что
коллинеарны,
поэтому найдётся такое числоt,
что ![]() ,
где множительt может
принимать любое числовое значение в
зависимости от положения точки M на
прямой. Множитель t называется
параметром. Обозначив радиус-векторы
точек М1 и М соответственно
через
,
где множительt может
принимать любое числовое значение в
зависимости от положения точки M на
прямой. Множитель t называется
параметром. Обозначив радиус-векторы
точек М1 и М соответственно
через ![]() и
и![]() ,
получаем
,
получаем![]() .
Это уравнение называетсявекторным уравнением
прямой. Оно показывает, что каждому
значению параметра t соответствует
радиус-вектор некоторой точки М,
лежащей на прямой.
.
Это уравнение называетсявекторным уравнением
прямой. Оно показывает, что каждому
значению параметра t соответствует
радиус-вектор некоторой точки М,
лежащей на прямой.
Запишем
это уравнение в координатной форме.
Заметим, что ![]() ,
,![]() и
и![]() отсюда
отсюда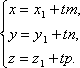
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Пусть М1(x1, y1, z1)
– точка, лежащая на прямой l,
и ![]() –
её направляющий вектор. Вновь возьмём
на прямой произвольную точкуМ(x,y,z) и
рассмотрим вектор
–
её направляющий вектор. Вновь возьмём
на прямой произвольную точкуМ(x,y,z) и
рассмотрим вектор ![]() .
.
Ясно,
что векторы ![]() и
и![]() коллинеарные,
поэтому их соответствующие координаты
должны быть пропорциональны, следовательно,
коллинеарные,
поэтому их соответствующие координаты
должны быть пропорциональны, следовательно,
![]() – канонические уравнения
прямой.
– канонические уравнения
прямой.
Замечание
1. Заметим,
что канонические уравнения прямой можно
было получить из параметрических,исключив
параметр t.
Действительно, из параметрических
уравнений получаем ![]() или
или![]() .
.
Пример. Записать
уравнение прямой ![]() в
параметрическом виде.
в
параметрическом виде.
Обозначим ![]() ,
отсюдаx =
2 + 3t, y =
–1 + 2t, z =
1 –t.
,
отсюдаx =
2 + 3t, y =
–1 + 2t, z =
1 –t.
Замечание
2. Пусть
прямая перпендикулярна одной из
координатных осей, например оси Ox.
Тогда направляющий вектор
прямой ![]() перпендикуляренOx,
следовательно, m=0.
Следовательно, параметрические уравнения
прямой примут вид
перпендикуляренOx,
следовательно, m=0.
Следовательно, параметрические уравнения
прямой примут вид 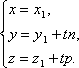
Исключая из уравнений параметр t, получим уравнения прямой в виде

Однако
и в этом случае условимся формально
записывать канонические уравнения
прямой в виде![]() .
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает,
что прямая перпендикулярна соответствующей
координатной оси.
.
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает,
что прямая перпендикулярна соответствующей
координатной оси.
Аналогично,
каноническим уравнениям ![]() соответствует
прямая перпендикулярная осямOx и Oy или
параллельная оси Oz.
соответствует
прямая перпендикулярная осямOx и Oy или
параллельная оси Oz.
Примеры.
Составить канонические и параметрические уравнения прямой, проходящей через точку М1(1;0;-2) параллельно вектору
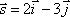 .
.
Канонические
уравнения: ![]() .
.
Параметрические
уравнения: 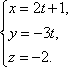
Составить уравнения прямой, проходящей через две точки М1(-2;1;3), М2(-1;3;0).
Составим
канонические уравнения прямой. Для
этого найдем направляющий вектор ![]() .
Тогдаl:
.
Тогдаl: ![]() .
.
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями
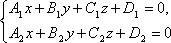
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.
Примеры.
Построить
прямую, заданную уравнениями ![]()
Для
построения прямой достаточно найти
любые две ее точки. Проще всего выбрать
точки пересечения прямой с координатными
плоскостями. Например, точку пересечения
с плоскостью xOy получим
из уравнений прямой, полагая z=
0: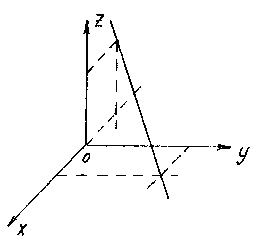
![]()
Решив эту систему, найдем точку M1(1;2;0).
Аналогично, полагая y= 0, получим точку пересечения прямой с плоскостью xOz:
![]()
От
общих уравнений прямой можно перейтик
её каноническим или параметрическим
уравнениям. Для этого нужно найти
какую-либо точку М1 на
прямой и направляющий вектор ![]() прямой.
прямой.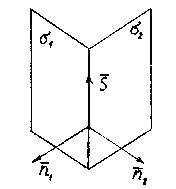
Координаты
точки М1 получим
из данной системы уравнений, придав
одной из координат произвольное значение.
Для отыскания направляющего вектора,
заметим, что этот вектор должен быть
перпендикулярен к обоим нормальным
векторам ![]() и
и![]() .
Поэтому за направляющий вектор
.
Поэтому за направляющий вектор![]() прямойl можно
взять векторное произведение нормальных
векторов:
прямойl можно
взять векторное произведение нормальных
векторов:
 .
.
Пример. Привести
общие уравнения прямой ![]() к
каноническому виду.
к
каноническому виду.
Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y= 0 и решим систему уравнений:
![]()
Нормальные
векторы плоскостей, определяющих прямую
имеют координаты ![]() Поэтому
направляющий вектор прямой будет
Поэтому
направляющий вектор прямой будет
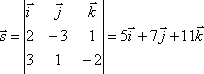 .
Следовательно, l:
.
Следовательно, l: ![]() .
.
УГОЛ МЕЖДУ ПРЯМЫМИ
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:

Очевидно,
что за угол φ между прямыми можно принять
угол между их направляющими векторами ![]() и
и![]() .
Так как
.
Так как![]() ,
то по формуле для косинуса угла между
векторами получим
,
то по формуле для косинуса угла между
векторами получим
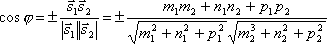 .
.
Условия
параллельности и перпендикулярности
двух прямых равносильны условиям
параллельности и перпендикулярности
их направляющих векторов ![]() и
и![]() :
:
Две
прямые параллельны тогда
и только тогда, когда их соответствующие
коэффициенты пропорциональны,
т.е. l1 параллельна l2 тогда
и только тогда, когда ![]() параллелен
параллелен![]() .
.
Две
прямые перпендикулярны тогда
и только тогда, когда сумма произведений
соответствующих коэффициентов равна
нулю: ![]() .
.
Примеры.
Найти угол между прямыми
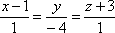 и
и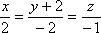 .
.
![]()
Найти уравнения прямой проходящей через точку М1(1;2;3) параллельно прямой l1:
![]()
Поскольку искомая прямая l параллельна l1, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l1.
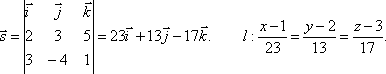
Составить уравнения прямой, проходящей через точку М1(-4;0;2) и перпендикулярной прямым:
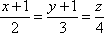 и
и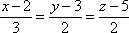 .
.
Направляющий
вектор прямой l можно
найти как векторное произведение
векторов ![]() и
и![]() :
:

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
![]()
Рассмотрим
векторы ![]() и
и![]() .
Если угол между ними острый, то он
будет
.
Если угол между ними острый, то он
будет![]() ,
где φ – угол между прямой и плоскостью.
Тогда
,
где φ – угол между прямой и плоскостью.
Тогда![]() .
.
Если
угол между векторами ![]() и
и![]() тупой,
то он равен
тупой,
то он равен![]() .
Следовательно
.
Следовательно![]() .
Поэтому в любом случае
.
Поэтому в любом случае![]() .
Вспомнив формулу вычисления косинуса
угла между векторами, получим
.
Вспомнив формулу вычисления косинуса
угла между векторами, получим .
.
Условие
перпендикулярности прямой и
плоскости. Прямая
и плоскость перпендикулярны тогда и
только тогда, когда направляющий вектор
прямой ![]() и
нормальный вектор
и
нормальный вектор![]() плоскости
коллинеарны, т.е.
плоскости
коллинеарны, т.е.![]() .
.
Условие
параллельности прямой и плоскости. Прямая
и плоскость параллельны тогда и только
тогда, когда векторы ![]() и
и![]() перпендикулярны.
перпендикулярны.
![]()
Примеры.
Написать уравнение плоскости, проходящей через точку М1(2;-3;4) параллельно прямым
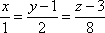 и
и .
.
Так как M1Î α, то уравнение плоскости будем искать в виде
![]() .
.
Применяя
условие параллельности прямой и
плоскости, получим систему линейных
уравнений ![]()
Отсюда
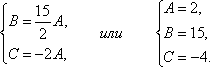
Итак, ![]() или
или![]() .
.
Найти угол между прямой
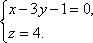 и
плоскостью
и
плоскостью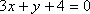 .
.
Направляющий
вектор прямой  .
Нормальный вектор плоскости
.
Нормальный вектор плоскости![]() .
Следовательно,
.
Следовательно,![]()
Найдите точку, симметричную данной М(0;-3;-2) относительно прямой
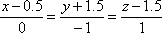 .
.
Составим
уравнение плоскости α перпендикулярной l. MÎ α, ![]() .
Следовательно,
.
Следовательно,![]() или
или![]() .
.
Найдём точку пересечения прямой l и α:
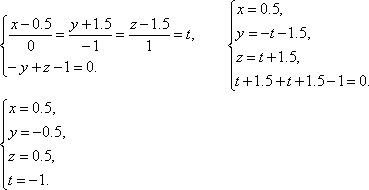
Итак, N(0.5;-0.5;0.5).
Пусть искомая точка М1 имеет
координаты М1(x,y,z).
Тогда очевидно равенство векторов ![]() ,
т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5).
Откуда x=1, y=2, z=3
или М1(1;2;3)..
,
т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5).
Откуда x=1, y=2, z=3
или М1(1;2;3)..
Точка пересечения прямой и плоскости
Рассмотрим
пошаговую инструкцию построения точки
пересечения прямой общего положения с
плоскостью общего положения.Отметим,
что построение точки пересечения прямой
и плоскости - это одна из основ решения
задач по предметуначертательная
геометрия,
не освоив которую дальнейшее понимание
предмета будет достаточно трудным.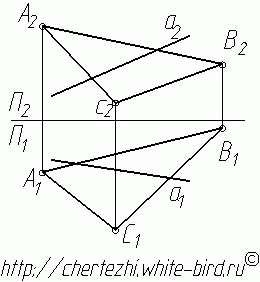
Порядок построения точки пересечения прямой и плоскости
1. Заключим прямую а во вспомогательную фронтально-проецирующую плоскость (плоскость перпендикулярную фронтальной плоскости проекции). На фронтальной проекции она сольется с прямой а. Очевидно, что линия mпересечения этой плоскости с плоскостью треугольника АВС на фронтальной проекции так же будет сливаться с прямой а (а=m). 2. Определим фронтальные проекции двух точек этой линии m: точки 1 и 2. 3. Найдем их горизонтальные проекции. 4. Соединим горизонтальные проекции точек 1 и 2 - получим горизонтальную проекцию прямой m (которая является линией пересечения вспомогательной плоскости с плоскостью треугольника АВС, и соответственно принадлежит обеим плоскостям). Так как прямая а принадлежит вспомогательной плоскости, и прямая mпринадлежит ей же, то точка пересечения этих прямых К и есть точка пересечения прямой а с плоскостью треугольника АВС. 5. С помощью линии связи найдем фронтальную проекцию точки пересечения К. 6. Осталось только определить видимость прямой а. Это можно сделать с помощью метода конкурирующих точек.
Обратите внимание, что мы начали поиск точки пересечения прямой с плоскостью с того, что заключили прямую а во вспомогательную фронтально-проецирующую плоскость. Точно таким же образом можно было заключить прямую а в горизонтально-проецирующую плоскость, и тогда бы построения начались как бы "снизу вверх", но смысл остался бы точно таким же, как и конечное решение - точка пересечения прямой с плоскостью.
Линии 2-го порядка
1.Эллипс.
Эллипсом наз-ся геометрическое место точек пл-ти, сумма расстояний от которых до двух данных точек пл-ти F1 и F2(фокусов) есть величина постоянная.
Составим
ур-е эллипса, считая известными
величинами: ![]() расстояний
2а от
расстояний
2а от![]() точки
эллипса до фокуса; расстояние между
фокусами. Отнесем пл-ть, в кот. расположен
эллипс, к декартовой системе координат
ху. Начало координат расположим в
середине отрезка [F1,F2];
ось Х проведем через F1,F2.
Пусть М(х,у) -
точки
эллипса до фокуса; расстояние между
фокусами. Отнесем пл-ть, в кот. расположен
эллипс, к декартовой системе координат
ху. Начало координат расположим в
середине отрезка [F1,F2];
ось Х проведем через F1,F2.
Пусть М(х,у) - ![]() точка
эллипса. r1-расстояние
от т.М до F1,
r2-соответственно
до F2.
Тогда по определению эллипса r1+
r2=2а.
Учитывая, что r1=
точка
эллипса. r1-расстояние
от т.М до F1,
r2-соответственно
до F2.
Тогда по определению эллипса r1+
r2=2а.
Учитывая, что r1= ![]() ,а
r2=
,а
r2= ![]() ,
можем з записать:
,
можем з записать:![]() .
Это неявное ур-е эллипса.
.
Это неявное ур-е эллипса.
![]()
![]() r1 r2
r1 r2 ![]() ;
; ![]() ;
;
![]()
![]()
![]()
![]() F(-a;0)
F(a;0)
F(-a;0)
F(a;0) ![]() ;
;![]() ;
;![]() ;
;
a4-2a2xc+x2c2=a2x2-2a2xc+a2c2+a2y2; (c2-a2)x2-a2y2=a2(c2-a2); (a2-c2)x2+a2y2=a2(a2-c2).
По
св-ву сторон треугольника r1+r2>2c,
т.е. 2а>2с или а>c. Следовательно а2-с2>0.
Положим в2=а2-с2 и
разделим обе части последнего ур-я на
а2b2.
Придем к каноническому ур-ю эллипса: ![]() ,
b2=a2-c2 (1.1)
,
b2=a2-c2 (1.1)
Легко проверить, что т. М1(-x,-y),M2(-x,y),M3(x,-y) удовлетворяют ур-ю эллипса. Это означает, что у эллипса есть центр симметрии т. О(0;0) и оси симметрии ОХ,ОУ. Точки пересечения эллипса с осями симметрии наз-ся вершинами эллипса.
![]()
![]() Пусть
А1,А2 вершины,
лежащие на оси Х, а В1 и
В2 –вершины,
лежащие на оси У. Найдем координаты этих
точек. Положим в ур-ии у=0: х2=а2;
х1=а,
х2=-а.
Поэтому А1=(-а;0),
А2=(а;0),
аналогично В1=(0;-b),
B2=(0;b).
Отрезки, заключенные между вершинами
эллипса, наз-ся его осями:
А1А2-большая(фокальная),
В1В2-малая
ось. Отношение e=с/a
Пусть
А1,А2 вершины,
лежащие на оси Х, а В1 и
В2 –вершины,
лежащие на оси У. Найдем координаты этих
точек. Положим в ур-ии у=0: х2=а2;
х1=а,
х2=-а.
Поэтому А1=(-а;0),
А2=(а;0),
аналогично В1=(0;-b),
B2=(0;b).
Отрезки, заключенные между вершинами
эллипса, наз-ся его осями:
А1А2-большая(фокальная),
В1В2-малая
ось. Отношение e=с/a
![]() называют
эксцентриситетом. Т.к с<=а, то е<=1.
Если е=0, то с=0. B2 d
называют
эксцентриситетом. Т.к с<=а, то е<=1.
Если е=0, то с=0. B2 d
![]()
![]()
![]()
![]()
![]() Если
е=0, то с=0. В этом случае F1 и
F2 эллипса
находятся в начале координат A1 F1 F2 A2
Если
е=0, то с=0. В этом случае F1 и
F2 эллипса
находятся в начале координат A1 F1 F2 A2
и эллипс превращается в окружность R=a. Директрисами эллипса
наз-ют 2 прямые параллельные малой оси и отстоящие от нее на расстоянии B1
a/e.
Построим ур-е касательной к эллипсу в
т. М(х1,у1),
не совпадающей ни с вершиной А1,
ни с вершиной А2.
Пусть у=у(х)-явное ур-е эллипса в окрестности
т.М. Известно, что ![]() явл.
угловым коэффициентом касательной к
кривой у=у(х) при х=х1.
Определим
явл.
угловым коэффициентом касательной к
кривой у=у(х) при х=х1.
Определим ![]() :
воспользуемся
:
воспользуемся![]() .Продифференцировав
по х обе части тождества, придем к новому
тождеству:
.Продифференцировав
по х обе части тождества, придем к новому
тождеству:
![]() .
Для М(х1,у1):
.
Для М(х1,у1): ![]() .
Из последнего рав-ва найдем
.
Из последнего рав-ва найдем ![]() :
:![]()
Проведем
через т. М(х1,у1)
эллипса в пл. ОХУ прямую с угловым
коэффициентои ![]() :
:
у-у1= ![]() (х-х1);
у-у1=
(х-х1);
у-у1= ![]() (*y1a2);
y1ya2-y12a2+xx1b2-x12b2=0;
xx1b2+yy1a2=x12b2+y12a2 (:a2b2);
(*y1a2);
y1ya2-y12a2+xx1b2-x12b2=0;
xx1b2+yy1a2=x12b2+y12a2 (:a2b2); ![]() ;
;![]() -
ур-е касательной эллипса в точке касания
М(х1,у1).
-
ур-е касательной эллипса в точке касания
М(х1,у1).
2.Гипербола.
Гиперболой наз-ют геометрическое место точек пл-ти, разность расстояний от которых до 2 данных точек пл-ти F1 и F2(фокусов) есть величина постоянная.
![]()
![]()
![]() Известны
разность расстояний от фокусов до точек
гиперболы 2а и расстояние между фокусами
2с. Отнесем пл-ть, в которой расположена
гипербола, к декартовой системе координат
ОХУ. В начало координат О расположим
середину отрезка F1F2.
Ось Х проведем через фокусы F1(-c;0)
и F2(c;0).
Т. М-произвольная точка пл-ти.
Известны
разность расстояний от фокусов до точек
гиперболы 2а и расстояние между фокусами
2с. Отнесем пл-ть, в которой расположена
гипербола, к декартовой системе координат
ОХУ. В начало координат О расположим
середину отрезка F1F2.
Ось Х проведем через фокусы F1(-c;0)
и F2(c;0).
Т. М-произвольная точка пл-ти. ![]() .
Учитывая, что
.
Учитывая, что![]() ,
,![]() ;
то
;
то ![]() .
M(x,y)
.
M(x,y)
Избавляясь от радикалов, придем к каноническому виду r1 r2
![]() гиперболы:
гиперболы: ![]() ,
b2=c2-a2 (2.1) F1 F2
,
b2=c2-a2 (2.1) F1 F2

![]() При
замене х на (-х) или у на (-у) ур-е гиперболы
не меняется, значит О- центр симметрии,
а оси координат- оси симметрии. Точки
пересечения А1 и
А2 гиперболы
с осью Х называют вершинами гиперболы.
Отрезок А1А2-
действительная ось, В1В2-мнимая
ось.
При
замене х на (-х) или у на (-у) ур-е гиперболы
не меняется, значит О- центр симметрии,
а оси координат- оси симметрии. Точки
пересечения А1 и
А2 гиперболы
с осью Х называют вершинами гиперболы.
Отрезок А1А2-
действительная ось, В1В2-мнимая
ось.
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 F1F2≥A1A2
F1F2≥A1A2 ![]() >1;
>1;![]() =e;
сопряженнаяd
=e;
сопряженнаяd
![]()
![]()
![]()
![]() 2c
2c ![]() 2a
директрисы:
2a
директрисы:![]() ;
B2
;
B2
![]()
![]() c≥a;
F1 A1 A2 F2
c≥a;
F1 A1 A2 F2
Запишем явное ур-е верхней части правой ветки гиперболы,
считая что х≥а и у≥0 для рассматриваемой части. Из канонического B1 директрисы
ур-я
гиперболы получаем искомое явное
уравнение: ![]() .
Рассматриваемая часть гиперболы
расположена ниже прямой
.
Рассматриваемая часть гиперболы
расположена ниже прямой ![]() .
При х→∞:
.
При х→∞: ![]() →1
→1 ![]() ветвь
гиперболы будет при х→∞
приближаться
к
прямой
ветвь
гиперболы будет при х→∞
приближаться
к
прямой ![]() так,
что расстояние между точками прямой и
гиперболы с одинаковыми абсцис. будет
→0
при
х→∞.
Прямая
так,
что расстояние между точками прямой и
гиперболы с одинаковыми абсцис. будет
→0
при
х→∞.
Прямая ![]() наз-ся
асимптотой гиперболы. А в силу симметрии
гиперболы относительно осей х и у ее
асимптотой будет прямая
наз-ся
асимптотой гиперболы. А в силу симметрии
гиперболы относительно осей х и у ее
асимптотой будет прямая ![]() .
Гипербола
.
Гипербола![]() наз-ся
сопряженной к гиперболе (2.1). Касательная
к гиперболе (2.1) в т. М(х1,у1)
имеет ур-е:
наз-ся
сопряженной к гиперболе (2.1). Касательная
к гиперболе (2.1) в т. М(х1,у1)
имеет ур-е: ![]() (2.2)
(2.2)
3.Парабола.
Параболой наз-ют геометрическое место точек пл-ти, равноудаленных от данной точки F(фокуса) и данной прямой(директриса).
Проведем
на пл-ти, в которой расположена парабола,
ось Х через F ![]() директрисе.
Через ось У декартовой системы проведем║
директрисе
между
F и
директрисой
на
расстоянии
р/2
от
F, где
р
- расстояние
между
фокусом
и
директрисой.
директрисе.
Через ось У декартовой системы проведем║
директрисе
между
F и
директрисой
на
расстоянии
р/2
от
F, где
р
- расстояние
между
фокусом
и
директрисой.
![]()
![]()
![]()
![]()
![]()
 r
=x+
r
=x+ ![]() .
по определению r=d.
.
по определению r=d.![]() d
M(x,y) r
d
M(x,y) r
![]() x2-px+
x2-px+ ![]() +y2=x2+px+
+y2=x2+px+ ![]() ;
е=
;
е=![]() =1;
y2=2px
– канонич. ур-е параболы 0 F(p/2;0)
=1;
y2=2px
– канонич. ур-е параболы 0 F(p/2;0)
Парабола симметрична относительно ОХ. x=-p/2
Ур-е касател-й к параболе, проходящей через т. М1, имеет вид: уу1=р(х+х1).
Общее ур-е кривой 2-го порядка: а11х2+2а12ху+а22у2+2а13х+2а23у+а33=0. Дискриминант кривой (Δ):
 ,
, ![]() ;
дискриминантом старших членов кривой
2-го порядка(δ):
;
дискриминантом старших членов кривой
2-го порядка(δ):![]()
|
|
Δ |
Δ=0 |
|
δ>0 |
эллипс(действ. или мним.) |
мнимые прямые, пересек. в одной точке |
|
δ =0 |
парабола |
║прямые(действ., мним., совпадающ.) |
|
δ <0 |
гипербола |
действит. пересек. прямые |
