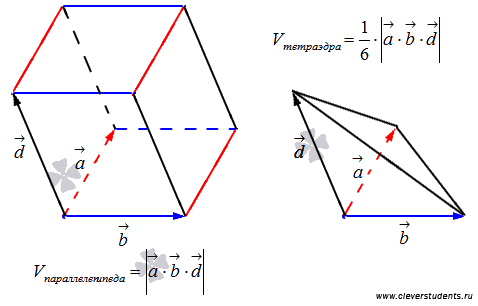
Смешанное произведение векторов и его свойства

Смешанным произведением векторов называется число, равное скалярному произведению векторана векторное произведение векторови. Смешанное произведение обозначается.

Геометрические свойства смешанного произведения

1. Модуль смешанного произведения некомпланарных векторов равен объемупараллелепипеда, построенного на этих векторах. Произведениеположительно, если тройка векторов— правая, и отрицательно, если тройка— левая, и наоборот.

2. Смешанное произведение равно нулю тогда и только тогда, когда векторыкомпланарны:

 векторы компланарны.

Докажем первое свойство. Найдем по определению смешанное произведение: , где— угол между векторамии. Модуль векторного произведения (по геометрическому свойству 1) равен площадипараллелограмма, построенного на векторахи: . Поэтому. Алгебраическое значениедлины проекции векторана ось, задаваемую вектором, равно по модулю высотепараллелепипеда, построенного на векторах(рис. 1.47). Поэтому модуль смешанного произведения равен объемуэтого параллелепипеда:

Знак смешанного произведения определяется знаком косинуса угла . Если тройкаправая, тои смешанное произведениеположительно. Если же тройкалевая, тои смешанное произведениеотрицательно.

Докажем второе свойство. Равенство возможно в трех случаях:или(т.е.),или(т.е. векторпринадлежит плоскости векторови). В каждом случае векторыкомпланарны (см. разд. 1.1).

Смешанным произведением трех векторов называется число, равное векторному произведению первых двух векторов,, умноженному скалярно на вектор. Векторами это можно представить так

Так как векторы на практике задают в координатной форме, то их смешанный произведение равен определитель, построенном на их координатам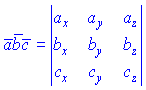В силу того, что векторное произведение антикомутативно, а скалярное произведение коммутативно, то циклическая перестановка векторов в смешанном произведении не изменяет его значение. Перестановка двух соседних векторов меняет знак на противоположный

Смешанный произведение векторов положительный, если они образуют правую тройку и отрицательный - если левую.

Геометрические свойства смешанного произведения1. Объем параллелепипеда, построенного на векторах равен модулю смешанного произведения этих векторов.2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения3. Объем треугольной пирамиды равен одной шестой модуля смешанного произведения4. Векторы планарных тогда и только тогда, когдаВ координатах условие компланарности означает равенство нулю определителя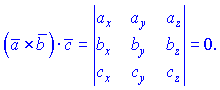Для практического усвоения рассмотрим примеры. Пример 1.

Определить, какой тройкой (правой или левой) являются векторы

Решение.

Найдем смешанное произведение векторов и по знаку выясним, какую тройку векторов они образуют

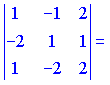
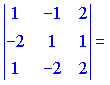
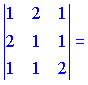
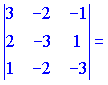
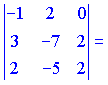
Векторы образуют правую тройку Векторы образуют правую тройкуВекторы образуют левую тройкуВекторы образуют правую тройкуВекторы образуют левую тройкуДанные векторы линейно зависимы.. Смешанным произведением трех векторов.  Смешанным произведением трех векторов называется число

Геометрическое свойство смешанного произведения:

Теорема 10.1.Объём параллелепипеда, построенного на векторах равен модулю смешанного произведения этих векторов

,

или объём тетраэдра (пирамиды), построенного на векторах равен одной шестой модуля смешанного произведения

.

Доказательство. Из элементарной геометрии известно, что объём параллелепипеда равен произведению высоты на площадь основания

Площадь основания параллелепипеда S равна площади параллелограмма, построенного на векторах (см. рис. 1). Используя

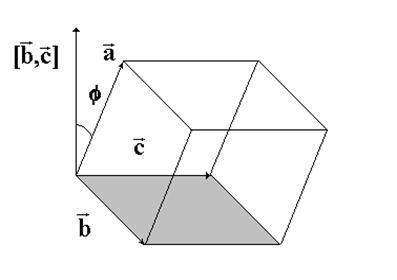Рис. 1. К доказательству теоремы 1. геометрический смысл векторного произведения векторов , получаем, что

.

Далее, если тройка векторов является правой (как на рис. 1), то высота параллелепипеда равна проекции векторана вектор, т.е.

Отсюда получаемЕсли тройка векторов левая, то вектор и вектор направлены противоположно, тогдаилиТаким образом, попутно доказано, что знак смешанного произведения определяет ориентацию тройки векторовтройка правая и ‑ тройка левая). Докажем теперь вторую часть теоремы. Из рис. 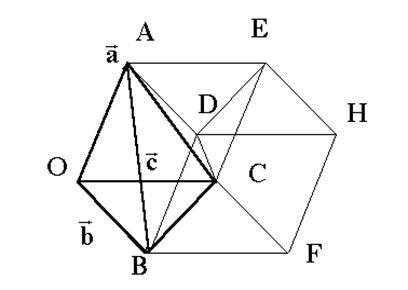2 очевидно, что объем треугольной призмы, построенной на трех векторахравен половине объема параллелепипеда, построенного на этих векторах, то есть Рис. 2. К доказательству теоремы 1.

Но призма состоит из трех одинакового объема пирамид OABC, ABCD и ACDE. Действительно, объемы пирамид ABCD и ACDE равны, так как они имеют равные по площади основания BCD и CDE и одинаковую высоту, опущенную из вершины A. То же справедливо для высот и оснований пирамид OABC и ACDE. Отсюда