Расстояние от точки до прямой на плоскости.

Формула для вычисления расстояния от точки до прямой на плоскости

Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(M_x, M_y) до прямой можно найти, используя следующую формулу

d =	|A·Mx + B·My + C|
	√A2 + B2

Примеры задач на вычисление расстояния от точки до прямой на плоскости

Пример 1.

 Найти расстояние между прямой 3x + 4y - 6 = 0 и точкой M(-1, 3).

Решение. Подставим в формулу коэффициенты прямой и координаты точки

d =	|3·(-1) + 4·3 - 6|	=	|-3 + 12 - 6|	=	|3|	= 0.6
	√32 + 42		√9 + 16		5

Ответ: расстояние от точки до прямой равно 0.6.

уравнение плоскости проходящей через точки перпендикулярно векторуОбщее уравнение плоскости

Ненулевой вектор , перпендикулярный заданной плоскости, называетсянормальным вектором (или, короче, нормалью) для этой плоскости.

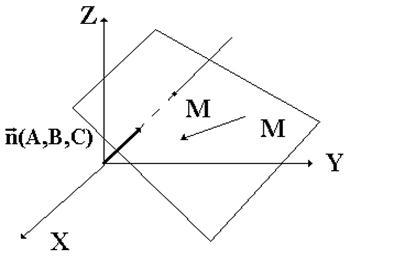
Пусть в координатном пространстве (в прямоугольной системе координат) заданы:

а) точка ;

б) ненулевой вектор (рис.4.8,а).

Требуется составить уравнение плоскости, проходящей через точку перпендикулярно векторуКонец доказательства.

Рассмотрим теперь различные типы уравнений прямой на плоскости.

1) Общее уравнение плоскости P.

Из вывода уравнения следует, что одновременно A, B и C не равны 0 (объясните почему).

Точка принадлежит плоскостиP только в том случае, когда ее координаты удовлетворяют уравнению плоскости. В зависимости от коэффициентов A, B, C и Dплоскость P занимает то или иное положение:

‑ плоскость проходит через начало системы координат, ‑ плоскость не проходит через начало системы координат,

‑ плоскость параллельна оси X,

‑ плоскость не параллельна оси X,

‑ плоскость параллельна оси Y,

‑ плоскость не параллельна оси Y,

‑ плоскость параллельна оси Z,

‑ плоскость не параллельна оси Z.

Докажите эти утверждения самостоятельно.

 

Уравнение (6) легко выводится из уравнения (5). Действительно, пусть точка лежит на плоскости P. Тогда ее координаты удовлетворяют уравнениюВычитая из уравнения (5) уравнение (7) и группируя слагаемые, получим уравнение (6). Рассмотрим теперь два вектора с координатами соответственно. Из формулы (6) следует, что их скалярное произведение равно нулю. Следовательно, вектор перпендикулярен вектору Начало и конец последнего вектора находятся соответственно в точках которые принадлежат плоскости P. Следовательно, вектор перпендикулярен плоскости P. Расстояние от точкидо плоскости P, общее уравнение которой определяется по формуле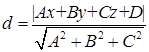Доказательство этой формулы полностью аналогично доказательству формулы расстояния между точкой и прямой (см. рис. 2).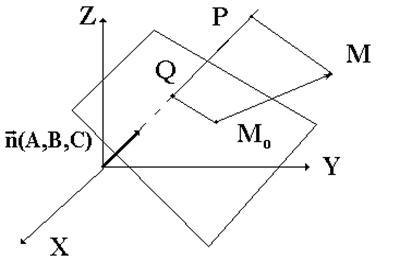Рис. 2. К выводу формулы расстояния между плоскостью и прямой.

Действительно, расстояние d между прямой и плоскостью равно

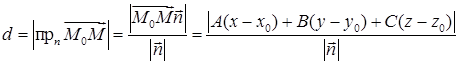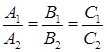
где ‑ точка лежащая на плоскости. Отсюда, как и в лекции № 11, получается выше приведенная формула. Две плоскости параллельны, если параллельны их нормальные вектора. Отсюда получаем условие параллельности двух плоскостей‑ коэффициенты общих уравнений плоскостей . Две плоскости перпендикулярны, если перпендикулярны их нормальные вектора, отсюда получаем условие перпендикулярности двух плоскостей, если известны их общие уравнения

 (10)

Угол f между двумя плоскостями равен углу между их нормальными векторами (см. рис. 3) и может, поэтому, быть вычислен по формуле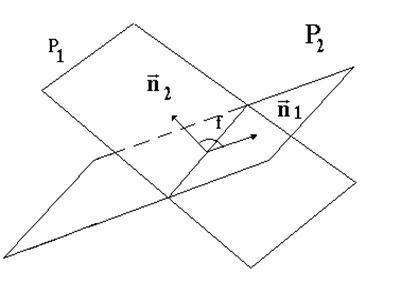 Определение угла между плоскостями.

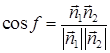 (11)

Расстояние от точки до плоскости и способы его нахождения

Расстояние от точки до 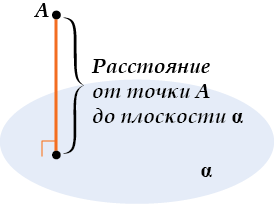плоскости – длина перпендикуляра, опущенного из точки на эту плоскость. Существует, по крайней мере, два способа найти расстояние от точки до плоскости:геометрический и алгебраический.

При геометрическом способе нужно сначала понять, как расположен перпендикуляр из точки на плоскость: может он лежит в какой –то удобной плоскости, является высотой в какой-нибудь удобном (или не очень) треугольнике, а может этот перпендикуляр вообще является высотой в какой-нибудь пирамиде.

После этого первого и самого сложного этапа задача распадается на несколько конкретных планиметрических задач (быть может, в разных плоскостях).

При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно ввести систему координат, найти координаты точки и уравнение плоскости, и после этого применить формулу расстояния от точки до плоскости.

Кажется с первого взгляда, что алгебраический способ легче, но это… далеко не всегда так. Проблемы обычно возникают как раз с нахождением координат точки и управления плоскости, особенно если система координат была введена не самым удобным способом. Для удобства приведём плюсы и минусы обоих способов в табличке: