Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой

Определение. Прямая, проходящая через точку М₁ (х₁ , у₁ ) и перпендикулярная к прямой у = kx + b представляется уравнением:

 

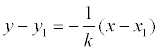
Расстояние от точки до прямой

Теорема. Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

.

Доказательство. Пусть точка М ₁(х ₁, у ₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁ :

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М ₀ перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x – x ₀ ) + B(y – y₀ ) + Ax₀ + By₀ + C = 0,

то, решая, получим: Подставляя эти выражения в уравнение (1), находим:

Угол между двумя прямыми.

. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

Посмотрим, как эта формула работает на конкретных примерах:

Угол между двумя прямыми

30 мая 2011

Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

Посмотрим, как эта формула работает на конкретных примерах:

Задача. В кубе ABCDA₁B₁C₁D₁ отмечены точки E и F — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AE и BF.

Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.

Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E — середина отрезка A₁B₁, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).

Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B₁C₁. Имеем: BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).

Итак, направляющие векторы готовы. Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:

Задача. В правильной трехгранной призме ABCA₁B₁C₁, все ребра которой равны 1, отмечены точки D и E — середины ребер A₁B₁ и B₁C₁соответственно. Найдите угол между прямыми AD и BE.Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA₁. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых.

Для начала найдем координаты вектора AD. Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1), т.к. D — середина отрезка A₁B₁. Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).

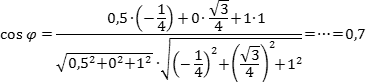Теперь найдем координаты вектора BE. Точка B = (1; 0; 0) считается легко. С точкой E — серединой отрезка C₁B₁ — чуть сложнее. Имеем:Осталось найти косинус угла:Задача. В правильной шестигранной призме ABCDEFA₁B₁C₁D₁E₁F₁, все ребра которой равны 1, отмечены точки K и L — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AK и BL.Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек:Точки K и L — середины отрезков A₁B₁ и B₁C₁ соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:

Теперь найдем косинус угла:Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.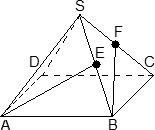Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1.

Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек: A = (0; 0; 0); B = (1; 0; 0)

Координаты вектора AE совпадают с координатами точки E, поскольку точка A — начало координат. Осталось найти косинус угла:

Условия параллельности и перпендикулярности прямых

Определение 1.Уравнением линии на плоскости Oxy называется уравнение F(x,y)=0, которому удовлетворяют координаты x и y каждой точки линии и только они.

Если из этого уравнения выразить переменную y, то получится уравнение y=f(x).

Если линии заданы уравнениями, то точкой пересечения двух линий называется любая точка, координаты x и y которой удовлетворяют уравнениям, т.е. являются решением системы двух уравнений.

Основные виды уравнений прямой на плоскости:

1) у=0 - уравнение оси Ох; y=b - уравнение прямой, параллельной оси Ох;

2) х=0 - уравнение оси Оу; х=а - уравнение прямой, параллельной оси Оу;

3) y=kх - уравнение прямой, проходящей через начало координат, с угловым коэффициентом k=tga, где a- угол наклона прямой к оси Oх;

4) y=kх+b - уравнение прямой с угловым коэффициентом k=tga, где a- угол наклона прямой с положительным направлением оси Oх.

y-y₀=k(x-x₀) - уравнение прямой, проходящей через точку (x₀,y₀) и имеющей угловой коэффициент k.

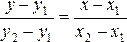уравнение прямой, проходящей через две данные точки (x₁,y₁) и (x₂,y₂) , если x₁¹x₂ и y₁¹y₂.

Определение 1.Уравнение с двумя переменными Ax + By + C = 0, где A и B не равны 0 одновременно, называется общим уравнением прямой на плоскости.

Теорема 1.Любая прямая на плоскости может быть задана общим уравнением.

Если В¹0, то 

т.е. y=кх+b . При этом: а) если А=0, то y=b;

б) если А=0 и С=0, то y=0;

в) если С=0, то y=кх .

Если В=0 и А¹0, то , т.е.х=а - если С¹0 и х=0 - если С=0.

Теорема доказана.

Точка пересечения двух прямых A₁x + B₁y + C₁ = 0и A₂x + B₂y + C₂ = 0есть решение системы линейных уравнений

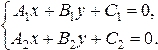
Пусть две прямые заданы уравнениями с угловыми коэффициентами y=к₁х+b₁ и y=к₂х+b₂, т.е. k₁=tga₁ и k₂=tga₂ , где a₁ и a₂ - углы наклона прямых к оси Ох.

Рассмотрим угол j=a₂-a₁ - угол между данными прямыми. Тогда, по формуле тангенса разности, 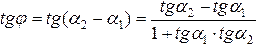, т.е..

Если прямые параллельны, то j = 0 , tgj = 0.

Итак, условием параллельности двух прямых является равенство их угловых коэффициентов, т.е. k₁= k₂ .

Если прямые перпендикулярны, то j = p/2 , ctgj = 0.

Итак, условием перпендикулярности двух прямых является равенство k₁× k₂ =-1.

Замечание.Можно показать, что если две прямые заданы общими уравнениями A₁x + B₁y + C₁ = 0и A₂x + B₂y + C₂ = 0, то:

условие параллельности прямых: ;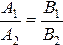

условие перпендикулярности прямых: A₁A₂ + B₁B₂ = 0.