- •3. На практике координаты векторов удобно представлять в виде матриц-столбцов (или матриц-строк), которые называются координатными столбцами (координатными строками).
- •Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора.
- •Скалярное произведение векторов и его свойства
- •7.3. Выражение векторного произведения через координаты
- •Угол между векторами
- •Смешанное произведение векторов и его свойства
- •Уравнение прямой на плоскости
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
- •Угол между двумя прямыми.
- •Угол между двумя прямыми
- •Расстояние от точки до прямой на плоскости.
- •Задача: в кубе abcd a1b1c1d1 с ребром 2 точки m — середина ребра a1d1. Найти расстояние от точки c до плоскости ab1mГеометрический способ.
- •Пусть плоскости p1 и p2 в пдск Оxyz заданы уравнениями:
- •§19. Взаимное расположение прямых и плоскостей в пространстве.
- •Гипербола: определение, свойства, построение
- •§ 121. Исследование формы параболы.
- •§ 123. Касательная к параболе.
- •§ 124. Оптическое свойство параболы.
- •§ 125. Полярное уравнение эллипса, гиперболы и параболы.
- •§ 126. Эллипс, гипербола и парабола как конические сечения.
§ 121. Исследование формы параболы.
Так
как ордината ![]() в
каноническое уравнение параболы входит
во второй степени, то ось
в
каноническое уравнение параболы входит
во второй степени, то ось![]() является
осью симметрии параболы
является
осью симметрии параболы![]() .
.
Определение. Точка
пересечения параболы с её осью симметрии
называется вершиной параболы. Парабола
(1) имеет только одну вершину ![]() .
.
Из
уравнения ![]() следует,
что
следует,
что![]() (т.к.
(т.к.![]() ,
а
,
а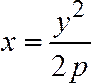 ).
Разрешая уравнение
).
Разрешая уравнение![]() относительно
относительно![]() и
беря для
и
беря для![]() лишь
неотрицательное значение
лишь
неотрицательное значение![]() ,
видим, что в полуинтервале
,
видим, что в полуинтервале![]()
![]() -
возрастающая функция
-
возрастающая функция![]() ,
причём
,
причём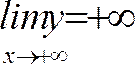 .
.
Всякая прямая пересекает параболу не более чем в двух точках (т.к. прямая определяется уравнением первой степени, а парабола - второй. Проведённое исследование даёт представление о форме параболы (См. рис. 177).
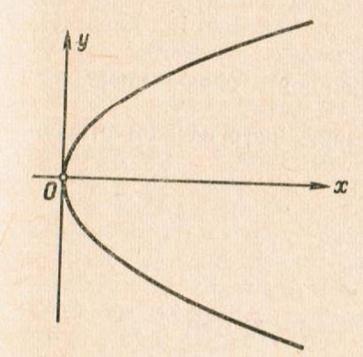
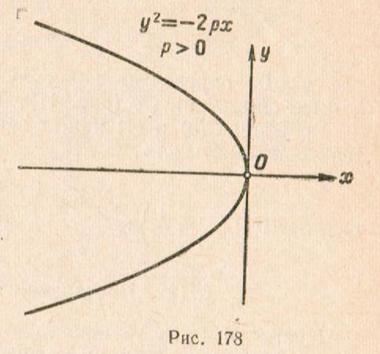
Рис. 177
Замечание. Уравнение ![]() ,
где
,
где![]() сводится
к уравнению
сводится
к уравнению![]() заменой
заменой![]() на
на![]() ,
т.е. путём преобразования системы
координат, которое соответствует
изменению положительного направления
оси
,
т.е. путём преобразования системы
координат, которое соответствует
изменению положительного направления
оси![]() на
противоположное.
на
противоположное.
Отсюда
следует, что парабола ![]() симметрична
с параболой
симметрична
с параболой![]() относительно
оси
относительно
оси![]() (См.
рис.178). Аналогичными рассуждениями
устанавливаем, чтокаждое из
уравнений:
(См.
рис.178). Аналогичными рассуждениями
устанавливаем, чтокаждое из
уравнений:![]() ;
;![]() (2)
где
(2)
где![]() определяет
параболу с вершиной в начале координат
и осью симметрии
определяет
параболу с вершиной в начале координат
и осью симметрии![]() (См.
рис. 179, 180).
(См.
рис. 179, 180).
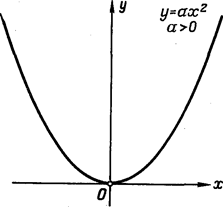
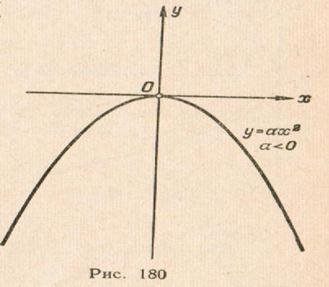
Рис. 179
Уравнение
(2) пишут часто в виде, разрешённом
относительно ординаты ![]() :
:![]() ,
где
,
где![]() ;
(
;
(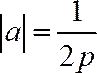 ).
).
§ 123. Касательная к параболе.
В
курсе математического анализа
доказывается, что если функция ![]() в
точке
в
точке![]() имеет
производную, то уравнение касательной
к линии, выражаемой уравнением
имеет
производную, то уравнение касательной
к линии, выражаемой уравнением![]() в
точке
в
точке![]() ,
где
,
где![]() имеет
вид:
имеет
вид:![]() .
Теперь, если парабола задана уравнением
.
Теперь, если парабола задана уравнением![]() ,
,![]() ,
то уравнение касательной к ней в
точке
,
то уравнение касательной к ней в
точке![]() будет
иметь вид:
будет
иметь вид:![]() .
Раскрываем скобки:
.
Раскрываем скобки:![]() ,
и, т.к.
,
и, т.к.![]() ,
откуда
,
откуда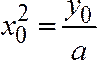 ,
то
,
то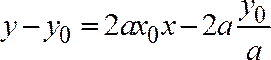 или
или![]() (3)
(3)
Полагая
в уравнении (3) ![]() ,
находим точку
,
находим точку![]() ,
пересечения касательной к параболе (3)
с её осью симметрии.
,
пересечения касательной к параболе (3)
с её осью симметрии.
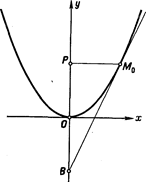
Отсюда
вытекает следующий способ построения
касательной к параболе в данной точке ![]() .
Опускаем из точки
.
Опускаем из точки![]() перпендикуляр
перпендикуляр![]() на
ось симметрии параболы и откладываем
на оси симметрии параболы отрезок
на
ось симметрии параболы и откладываем
на оси симметрии параболы отрезок![]() (См.
рис.). Прямая
(См.
рис.). Прямая![]() и
будет касательной к параболе в точке
и
будет касательной к параболе в точке![]() .
.
§ 124. Оптическое свойство параболы.
 Теорема
1. Касательная
к параболе является биссектрисой
угла
Теорема
1. Касательная
к параболе является биссектрисой
угла ![]() между
фокальным радиусом
между
фокальным радиусом![]() точки
касания и перпендикуляром
точки
касания и перпендикуляром![]() ,
опущенным из точки касания на директрису.
,
опущенным из точки касания на директрису.
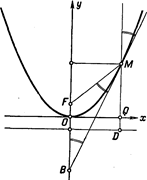
Рис. 183. Рис. 184.
Доказательство. Имеем
(См. рис. 184): ![]() ,
,![]() .
Но
.
Но![]() ,
,![]() .
Следо-вательно:
.
Следо-вательно:![]() ,
т.е.
,
т.е.![]() .
Поэтому треугольник
.
Поэтому треугольник![]() равнобедренный
и, значит:
равнобедренный
и, значит:![]() ;
но
;
но![]() ;
следовательно
;
следовательно![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Эта
теорема имеет следующее оптическое
истолкование: если в фокусе ![]() параболического
зеркала поместить источник света, то
лучи, отразившись от зеркала, образуют
пучок параллельных лучей. Указанное
свойство параболического зеркала
применяется при устройстве зеркальных
прожекторов.
параболического
зеркала поместить источник света, то
лучи, отразившись от зеркала, образуют
пучок параллельных лучей. Указанное
свойство параболического зеркала
применяется при устройстве зеркальных
прожекторов.
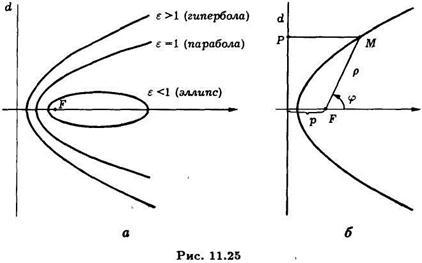
§ 125. Полярное уравнение эллипса, гиперболы и параболы.
Часто используют уравнения эллипса, гиперболы и параболы в полярной системе координат. Мы фиксируем полюс полярной системы координат в фокусе кривой. При этом для эллипса выбираем левый фокус, а для гиперболы - правый. Полярную ось выбираем так, чтобы её направление совпадало с положительным направлением оси абсцисс.
Все
три вида кривых описываются общим
свойством: для любой точки отношение
расстояний до фокуса и до директрисы
постоянно и равно эксцентриситету
кривой. Значение эксцентриситета
определяет тип кривой. Если зафиксировать
фокальный параметр (это расстояние от
фокуса до директрисы) так, что положение
директрисы в выбранной системе координат
будет оставаться неизменным, то варьируя
эксцентриситет, получим единый ряд
эллипсов, параболы, правых ветвей
гипербол (См. рис. 11.25). Конкретная кривая
определяется своим эксцентриситетом ![]() при
помощи уравнения:
при
помощи уравнения: ,
(4)
,
(4)
где ![]() -
полярный, он же фокальный радиус точки
-
полярный, он же фокальный радиус точки![]() на
кривой,
на
кривой,![]() -
перпендикуляр, опущенный из точки
-
перпендикуляр, опущенный из точки![]() на
директрису
на
директрису![]() (См.
рис. 11.25 ).
(См.
рис. 11.25 ).
|
|
Так
как ![]() ,
то подставив это выражение в (4),
получим:
,
то подставив это выражение в (4),
получим: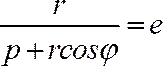 или
или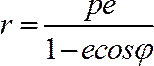 (5)
(5)
Уравнение (5) называется полярным уравнением эллипса, параболы, правой ветви гиперболы.